清华大学保研笔试题
版权声明：本文为博主原创文章，未经博主允许不得转载。博客不用于商业活动，博主对博客的使用，拥有最终解释权 本文为原创作品，未经本人同意，禁止转载，禁止用于商业用途！本人对博客使用拥有最终解释权 欢迎关注我的博客：http://blog.csdn.NET/hit2015spring和http://www.cnblogs.com/xujianqing/
又到了每年硕士推免生申请夏令营的时候了，在这里分享一下两年前（突然感觉自己好老），申请的清华大学的推荐免试研究生过程中的一个数学建模题目和自己写的一篇建模的文档，得到了该大学导师的不错的评价（有点吹牛逼）。虽然最后自己做了一个争（you）议（qian）满（kao）满（lv）的决定，但是还是分享给大家，写的不好不要骂我！轻喷！下面首先是题目，然后是我的论文吧！
界面检测算法
一、背景
回声测距仪可以检测洞穴中液位的深度,其主要利用声波回声原理测量气水界面距离洞口的精确距离。该动态液面距离的有效测量对许多生产活动和设备安全运行等具有重要意义。假设洞穴竖直向下延伸，洞穴中动态液面深度的测量使用回声（测深）测量方法，即在洞口放一枪（高压气枪），形成的声波向洞内传播, 遇到液面后反射, 测得声波的往返时间, 推算出液面深度。利用这种方法测距易受其他杂波干扰, 测量精度和深度受到了一定的限制。因此,人们为提高回波信号的信噪比，提出了很多方法处理回波信号如小波变换、硬件滤波、神经网络等。
二、具体要求
1. 声速在洞穴内传播过程中是会发生变化的，请建立声速在洞穴内传播时随温度，气体压力的变化模型（假设洞穴内充的是氮气）并利用Matlab程序进行模拟和仿真。假设液体界面位于洞口下方1010m左右深度，在洞口下方1000m处有一个回音标志物，它的深度位置已知，可以反射声波作为距离洞口深度的标定参考，液面在回音标志物下方10m左右的位置，但精确的位置并不清楚，需要依靠回声定位的方法检测液面回波进行测量。第一步请首先推导建立声音速度在井内变化的模型，并考虑如何有效利用这个唯一的回音标志物；
2. 液面反射的声波信号到达接收端，其中也夹杂着大量噪声，如何识别回音标志物的回波信号和分界液面的反射信号是一个模式识别和微弱信号检测的问题。根据回波特性设计一套回波的识别和检测算法，给出数学推导过程。
三、报告撰写与提交
1. 将撰写的研究报告、查找的参考文献和编写的Matlab程序打包，统一命名格式为：姓名+学校+专业+回声信号检测+联系电话，所有材料提交到指定邮箱
2. 请于接收到题目一周之内完成文献查阅和报告撰写等工作。
界面检测算法
摘要：回声测距仪可以检测洞穴中液位的深度,其主要是利用声波回声原理测量气/水界面距离洞口的精确距离。该动态液面距离的有效测量对许多生产活动和设备安全运行等具有重要意义。以此为背景提出了两个问题，声速随气压温度变化的关系和微弱信号检测分析。本文运用热力学定律，Johannes van der Waals修正公式，语音信号短时时域处理等方法解决了这两个问题。
关键词：温度 气压 声速修正 回声测距 模式识别 信号处理
Abstract：The echo ranger can test the depth of the liquid level in the cavern ,which mainly utilizes the acoustic echo principle to measure the gas / water interface from the hole of the exact distance. The effective measurement of dynamic liquid surface distance has important significance for many production activities and safe operation of equipment. Based on this background,two questions are raised, which relationship of sound velocity with air pressure, temperature and weak signal detection. In this paper, we use the laws of thermodynamics, Johannes van der Waals correction formula, speech signal short-time processing method to solve the two problems.
Key words: temperature, pressure, sound velocity correction, echo ranging, pattern recognition, signal processing.
目录
引言：
回声测距仪是利用声波反射原理测量水深的仪器。在洞口放一枪，形成声波向洞穴内部传播，遇到液面后形成反射波返回洞口，在洞口测得声波的往返时间就可得到液面距离洞口的深度。但在实际运用中，声速受到环境中的各种因素（温度、湿度、气压、气体的成分）的影响，还有声波信号易受环境中的杂波干扰，使测量的精度和深度受到限制。本文从声速的导出公式出发，考虑到影响声速的温度和气压因素，建立声速在氮气中的随温度气压变化的模型。再运用该模型提出测深的算法。最后在数字信号处理的基础上提出对回波信号进行处理，从而提取出测深算法所需的时间信息。
一、回声测深原理
当声波在介质中传播时，由于传播介质发生改变而发生反射现象，比如在空气中传播遇到液面时就会发生反射现象。回声测深仪就是利用了声波的反射原理来进行。所测得洞穴深度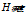
与声波在空气中传播速度
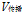及传播时间有关，即： 
。因为声速在洞穴中的传播过程是变化的，与温度气压等有关，因此很难得到声速在洞穴中的真实速度，无法得到真实的深度。故需建立声速模型。而传播时间则可通过测得回波信号时间获得。
二、声速模型
模型假设条件：
1、洞穴之内的环境条件只有气压和温度变化（湿度等因素不考虑）。
-
洞穴是竖直向下的，不存在弯曲。
-
洞穴内部的气体成分为纯氮气。
-
忽略声音在传播过程中因为被吸收而产生的速度变化。
-
洞穴内的温度与深度的函数关系已知为
。 -
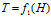洞穴内部的气压与深度的函数关系已知为
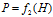。对模型中用到的符号进行说明（如表1）。
符号
意义
R
普适气体常数，8.314 J/（mol*K）
γ
氮气的比热容比，双原子分子为1.41
T
环境温度，（K）
M
氮气摩尔质量
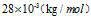
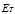
气体等温过程的弹性模数（
）
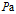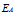
气体绝热过程的弹性模数（
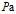）P
气压
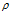
密度
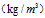
V
摩尔体积
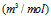
c
声速（m/s）
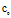
理想气体中声速（m/s）
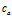
修正后的声速（m/s)
K
介质体积弹性模量
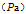
a
范德瓦尔斯修正数
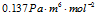
b
范德瓦尔斯修正数
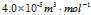
表1 符号说明表
引用参考文献【1】中的气体中声速传播的公式可以依照弹性波在连续介质中传播速度来计算：
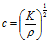(1)在运用声音在气体中传播的时更常用到式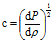（2）
(2)我们假定（1）气体中的声波传播是绝热过程（2）声音的传播振幅无限小于是
（1）式可以写成（3）式所示。
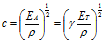(3)其中
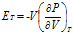
声音传播是绝热过程，故满足绝热方程式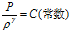（4）
（4）式（4）代入（2）中可得到声速传播拉普拉斯方程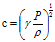（5）
(5) 把洞穴中的气体视为理想气体时，根据理想气体物态方程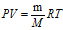（6）
(6) 可得到理想气体中的声速如（7）式
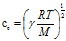(7) 实际气体在压强不太大，温度不太低的情形下近似遵循理想气体物态方程。当压强比较大，温度比较低时，气体分子的数密度n将比较大，分子本身的大小和分子间的引力就不能忽略不计。这与理想气体分子模型中的假设：把理想气体分子看作是可忽略其本身大小和分子间引力的自由质点矛盾。本文选择范德瓦尔斯首先导出的实际气体物态方程对理想状态下的声速进行修正。
Johannes van der Waals公式：
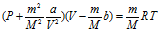(8) 得
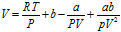(9) 在实际运用中
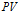可以近似用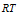
来代替，故可得公式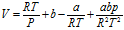(10)
(10) 代入(3)中可得到空气中声速的修正公式
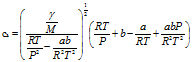(11)在气体压力为一个标准大气压（
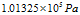）时声速随温度变化（如表2）。气体压力为
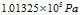时声速随温度变化温度（K）
理想气体声速m/s
修正气体声速m/s
差值m/s
300.0
354.4020
354.1890
0.2130
300.5
354.6972
354.4857
0.2115
301.0
354.9922
354.7822
0.2100
301.5
355.2869
355.0784
0.2086
302.0
355.5814
355.3743
0.2071
302.5
355.8756
355.6700
0.2056
303.0
356.1696
355.9654
0.2042
303.5
356.4634
355.2606
0.2027
304.0
356.7569
356.5556
0.2013
304.5
357.0501
356.8503
0.1999
305.0
357.3432
357.1447
0.1984
305.5
357.6359
357.4389
0.1970
306.0
357.9285
357.7329
0.1956
306.5
358.2208
358.0266
0.1942
307.0
358.5129
358.3201
0.1928
307.5
358.8047
358.6133
0.1914
308.0
359.0963
358.9063
0.1900
308.5
359.3876
359.1990
0.1886
309.0
359.6788
359.4915
0.1873
309.5
359.9696
359.7837
0.1859
310.0
360.2603
360.0757
0.1854
表2
所得到的曲线图（如图1）。
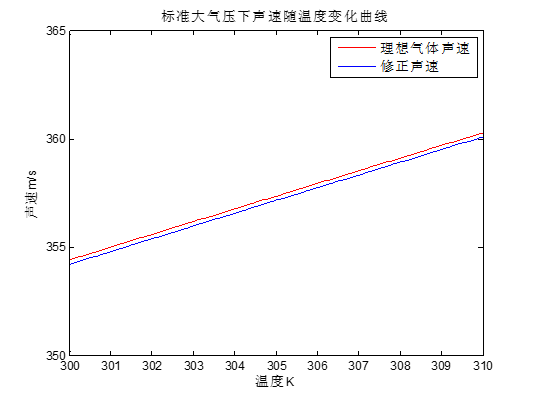
图1标准大气压声速—温度变化曲线
