k-means算法总结

1.原理

　　聚类是一种无监督学习的方法，其实质是依据某种距离度量，使得同一聚簇之间的相似性最大化，不同聚簇之间的相似性最小化，即把相似的对象放入同一聚簇中，把不相似的对象放到不同的聚簇中。聚类与分类不同，聚类的输入对象不需要带有类别标签，最后组成的分类是由使用的算法决定的。

在聚类中，k-means由于其简单、易实现的优点，被广泛使用。

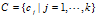　　假设集合是d维向量空间中的集合，其中表示集合中的第i个对象（或称为"数据点"），设矩阵表示k个聚簇中心的集合，其中，表示第j个聚簇标识，向量用于表示每个数据点所属的聚簇。

　　k-means算法是一种迭代的贪婪下降求解算法，其目标函数是非凸的，这也是造成只能得到局部最优解的原因，目标函数表达式如下：

　　算法的流程主要包括，首先我们随机选择集合中的k个点作为初始的聚簇中心，接着根据将集合中的每个点分配到距离它最近的聚簇中，最后根据每个聚簇中的数据点更新聚簇中心，如此反复地执行后两个步骤直到算法收敛。k-means算法就是通过迭代的方式，将集合中的数据点聚成k个类，其核心步骤主要有：

　　1）将数据点分配到距离它最近的聚簇中心

　　2）更新聚簇中心（取聚簇中每个数据点坐标的均值）

　　算法的详细步骤如表1所示，

表1 k-means算法的具体步骤

 

 

 

 2.缺陷

　　k-means算法存在不少的缺陷，表2列出了k-means算法常见的缺陷以及解决的方法。

表2 k-means算法缺陷

 

 

3.扩展

3.1核方法

　　为了能处理形状复杂的聚簇，我们可以通过核方法提高k-means算法对于复杂数据的处理能力。我们知道聚簇边界在原空间中是非线性的，但是，如果是在核函数所隐含的高维空间中却可以线性的。

3.2加速的k-means

　　k-means算法在处理超大数据时，存在时间过长的缺陷，所以针对这个缺点，提出了不少的改进算法。例如可以通过使用kd-树或者利用三角不等式，减少在重新划分聚簇这个步骤的计算量。

3.3柔性k-means

　　柔性k-means是与刚性k-means相对的，刚性的k-means即基本的k-means算法，将每个数据点划分到唯一一个聚簇中。而在柔性的k-means算法中，将每个数据点依据概率赋给每个聚簇，即柔性k-means中，每个数据点都有一个权重（概率）向量，用来描述每个数据点属于每个聚簇的可能性。

 

 4.小结

　　k-means算法使用简单的迭代将数据集聚成k个类，迭代的核心步骤有：（1）更新聚簇中心；（2）更新聚簇标识。尽管它有不少缺陷，但是其实现简单、移动、伸缩性良好等优点使得它成为聚类中最常用的算法之一。

 

参考文献

[1]Xindong Wu,Vipin Kumar.数据挖掘十大算法[M].北京：清华大学出版社.2014:19-30.