进化算法期末考试题目

题目：

小吃店的营业情况

　　某小吃店供应的一种特色点心很受欢迎，小吃店营业时间是上午8时至下午1时，顾客按表1所示规律到达该店。顾客往往是几个熟人一起来用点心的，经过一段时间的观察，每批顾客的人数如表2所示，每位顾客吃点心的份数如表3所示。每位顾客在小吃店的停留时间见表4，如有几个熟人一起进店用点心，则这群顾客在店中的停留时间是其中吃得最慢的顾客所停留的时间。

表1 顾客到达规律

顾客到达时间间隔/min	3	5	6	8	10
概率P	0.3	0.2	0.15	0.2	0.15

表2 每批顾客数

每批顾客人数/人	1	2	3	4
概率P	0.4	0.3	0.2	0.1

表3 每位顾客吃点心的份数

每位顾客吃点心的份数/份	1	2	3	4
概率P	0.4	0.3	0.2	0.1

表4 顾客停留时间

每位顾客停留的时间/min	10	15	20	25
概率P	0.1	0.4	0.3	0.2

 

　　请模拟小吃店5小时的营业情况，然后回答下列问题：

1. 平均每小时应准备多少份特色点心？
2. 每一批同时进店的顾客平均停留多长时间？

 

解：要回答第一个问题应求出5个小时准备的点心份数，即5个小时内顾客吃的点心份数，而第二个问题则应求出每批顾客的停留时间，在程序中，我们假设8点刚好是第一批顾客到来的时间，程序的流程图如图1所示。

图1 程序流程图

具体的程序如下：

 

close all;
clear;
clc;
load Data;
rand('state',sum(100*clock));


%% 参数初始化
iter_num = 300;
snack_mean = zeros(iter_num,1);
staytime = zeros(iter_num,100);
staytime_mean = zeros(iter_num,1);

% 主循环
for iter = 1:iter_num

　　%% 累计清零
　　time = 0;
　　snack_num = 0;
　　count = 0;

　　%% 求出第一批顾客的人数、吃的点心份数以及停留时间
　　count = count + 1;

　　% 使用轮盘赌的方式选择第一批顾客的人数
　　pos = find(table2_cum>=rand);
　　cus_num = table2(pos(1),1);
　　for i = 1:cus_num
　　　　pos = find(table3_cum>=rand);
　　　　snack_num = snack_num + table3(pos(1),1);
　　end

　　% 使用轮盘赌的方式求出第一批顾客的停留时间
　　staytime_tem = zeros(1,cus_num);
　　for i = 1:cus_num
　　　　pos = find(table4_cum>=rand);
　　　　staytime_tem(i) = table4(pos(1),1);
　　end
　　staytime(iter,count) = max(staytime_tem);

　　% 子循环
　　while time<=300

　　　　%% 求出下一批顾客的人数、吃的点心数以及停留的时间
　　　　count = count + 1;

　　　　% 求出下一批顾客到来的时间间隔并累计
　　　　pos = find(table1_cum>=rand);
　　　　time = time + table1(pos(1),1);

　　　　% 求出下一批顾客的人数
　　　　pos = find(table2_cum>=rand);
　　　　cus_num = table2(pos(1),1);

　　　　% 求出下一批顾客吃的点心数
　　　　for i = 1:cus_num
　　　　　　pos = find(table3_cum>=rand);
　　　　　　snack_num = snack_num + table3(pos(1),1);
　　　　end

　　　　% 求出下一批顾客的停留时间
　　　　staytime_tem = zeros(1,cus_num);
　　　　for i = 1:cus_num
　　　　　　pos = find(table4_cum>=rand);
　　　　　　staytime_tem(i) = table4(pos(1),1);
　　　　end
　　　　staytime(iter,count) = max(staytime_tem);
　　end

　　% 存放平均点心份数
　　snack_mean(iter) = snack_num/5;

　　% 存放平均每批顾客的停留时间
　　staytime_mean(iter) = sum(staytime(iter,:))/count;
end


%% 显示结果
mean1 = ceil(mean(snack_mean));
mean2 = round(mean(staytime_mean));
disp(['平均每小时应准备',num2str(mean1),'份点心']);
disp(['每批顾客平均停留时间为',num2str(mean2),'分钟']);


%% 画图
% 图1:平均每小时应准备的点心数随迭代次数的变化
figure(1);
plot(1:iter_num,snack_mean,'-xb');hold on;
plot(1:iter_num,mean1*ones(1,iter_num),'-r','LineWidth',2);
xlabel('迭代次数');
ylabel('平均每小时吃的点心份数');
title('平均每小时吃的点心份数随迭代次数的变化');

% 图2:每批顾客平均停留时间随迭代次数的变化
figure(2);
plot(1:iter,staytime_mean,'-xb');hold on;
plot(1:iter,mean2*ones(1,iter_num),'-r','LineWidth',2);
xlabel('迭代次数');
ylabel('每批顾客平均停留时间');
title('每批顾客平均停留时间随迭代次数的变化');

程序的结果如图2和图3所示，在图2中，蓝线表示平均每小时吃的点心份数随迭代次数的变化，而红线则是对平均点心份数作平均后的结果，从图中可以看出平均每小时吃的点心份数是42份，也就是说平均每小时应该准备42份的点心。在图3中，蓝线表示每批顾客平均停留时间随迭代次数的变化，而红线则是对平均停留时间作平均后的结果，从图中可以看出每批顾客的平均停留时间是20分钟左右。

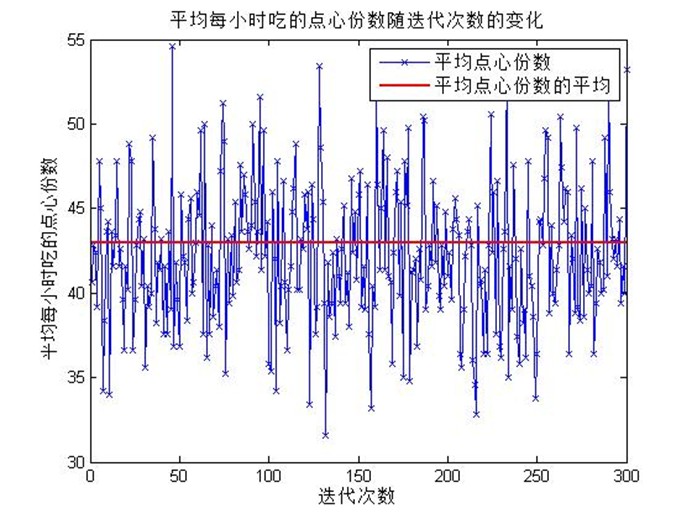
图2 平均每小时吃的点心份数随迭代次数的变化

图3 每批顾客平均停留时间随迭代次数的变化