[APIO2016] 划艇

https://www.luogu.com.cn/problem/P3643

https://loj.ac/p/2567

还在卡常，写了两天，醍醐灌顶的好题！

前言：感谢 wxy 老师的耐心指导。若有 \(F(x)\equiv G(x)\mod{p}\)，我们要求出 \(F(R)\mod p\)，但是给定的点值为 \((x,F(x)\mod p)\) 的形式，也就是给出的是 \((x,G(x))\)，那我们插值还是正确的吗？考虑插值的公式 \(H(x)=\sum\limits_{i}y_i\prod_{k\not =i}\dfrac{x-x_k}{x_i-x_k}\)，那么现在给定的并不是 \(y_i\)，而是 \(y_i\mod p\)，\(x_k\)，给定的也是 \(x_k\mod p\)，我们还能求出正确的答案吗？注意到本质上求的是 \(H(x)\mod p\)，那么你对于各个部分先取模，显然最后得到的也是对的。所以本质上我们并不是在插 \(G(x)\)，仍然可看作在插 \(F(x)\)，只是插最后的答案要 \(\mod p\) 而已。因此，我们仍然需要插 \(\deg(F(x))+1\) 个点。

问题难点在于加速如下方程。

\[f(i,j)=\begin{cases} \sum_{k=1}^j f(i-1,k),a_i\le j\le b_i\\ f(i-1,j),\text{otherwise}\\ \end{cases} \]

这里别当成函数，当成 \(f\) 数组。

我把第一个方程的操作称为类前缀和。

初始化为

\[f_0(0)=1 \]

\[f_0(k)=0,k\not =0 \]

我认为难点在于如何理解它是个 \(f_i\) 是个函数，且函数表达式为一个多项式，当然，有可能是个分段函数。

可通过数归来分析。

  1. 初始，可看成 \(f_0(x)=\begin{cases} 1,x=0 \\ 0,\text{otherwise} \\ \end{cases}\)，显然这是个分段函数，且每个函数表达式都是一个次数界为 \(1\) 的多项式。

  2. 转移，考虑到 \(i\) 的时候，\(f_i\) 可能已经被分成了若干段，各段均为一个表达式是多项式的函数，image

    如图，那么，考虑 \(a_{i+1},b_{i+1}\) 搞下去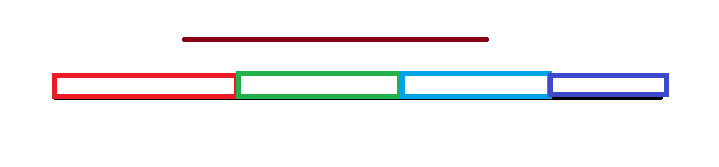，image
    会分裂常数个函数，也就是会新增常数个段，那么绿色这种完整覆盖的，显然其函数只是相当于做了一个类前缀和操作，但其定义域是没发生变化的，但其次数会 \(+1\)，下面会具体分析这个操作，对于紫色的，没被覆盖到，显然啥都没变化。对于红色，蓝色的，会其被棕色覆盖到的部分，会进行一次类前缀和的操作，因此其函数会不同于原先。

  3. 对一个多项式函数施类前缀和操作，只会让其次数 \(+1\)，并不会改变其是一个多项式的事实。
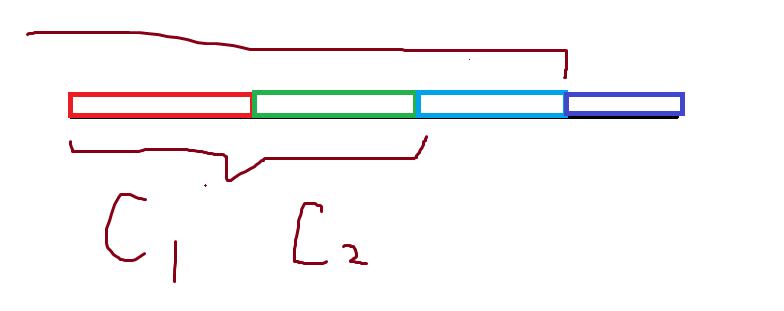
    image
    考虑对蓝色块进行前缀和，那么显然其 \(F(x)=C+\sum_{k\le x}f(x)\)，其中 \(C\) 为红色段与绿色段的和，然后这个东西升次了，可以用有限微积分来分析，当然积分直觉性地理解也可以，若有 \(G(x)=\int F(x)dx\)，则 \(\deg(G)=\deg(F)+1\)，然后对一个多项式积分之后显然还是一个多项式。

  4. 类前缀和操作只会操作整块。我们可以离散化端点，这样区间内的每个点受到的操作都是一样的了。

那么，到最后，\(f_n\) 一定是一个由 \(O(n)\) 个次数界为 \(n+1\) 的多项式组成的分段函数。

考虑咋做，对于离散化后的区间 \([l,r]\)，设其函数为 \(F_i(x)\)，这里有下标是因为我们要对于每个 \(i\)，求出 \(f(i,j)\)，因此其每个 \(i\) 的函数都不一样。那么为了转移，我们要求出 \(\sum\limits_{k=l}^r F(k)\)，那么显然要求出来 \(f(i,k),0\le i \le n,l\le k\le l+n\)，即插 \(n+1\) 个点，然后通过拉格朗日插值求出来，但是不是需要多点求值！显然，你再维护一个 \(g(i,j)=\sum_{l\le k\le j}f(i,k)\)，即可，又因为这个操作等价于类前缀和，所以 \(G_i(x)\) 为对 \(F_i(x)\) 求前缀和，注意，二者定义域都在 \([l,r]\)，插 \(n+2\) 个点就能求出来了。然后一些精细实现，本题难点并不在这。

一些实现注意点：

  1. 虽然插值共有 \(O(n^2)\) 次，但每 \(O(n)\) 次插的点的 \(x\) 都是一样的，因此可以预处理 \(\prod\)，单次均摊 \(O(n)\)。

  2. 因为我们对于每个 \(x\)，预先处理了 \(\prod x-x_k\)，因此 \(x-x_i\) 必须存在逆元，即其不为 \(0\)，否则的话可以特判规避下，即若区间长度 \(<=n+1\) 直接暴力，否则直接插，因为 \(p\) 很大，因此我们这样是对的。

#include <bits/stdc++.h>
//#define int long long
#define pb push_back
#define ADD(x,y) (((x)+(y)>=mod?(x)+((y)-mod):((x)+(y))))
using namespace std;
const int N=520,mod=(int)(1e9+7),M=(int)(5e6+5);
int f[N][N],g[N][N];
int sum[N],lsh[N*100],tot,a[N],b[N],k,n;

int fpow(int x,int y) {
	int res=1; x%=mod;
	while(y) {
		if(y&1) res=1ll*res*x%mod;
		y>>=1; x=1ll*x*x%mod; 
	} return res;
}

int X[N],Y[N],cnt,p[N],q[N],pre[N],r1;
int F(int x) {
//	cout<<"usd";
	int res=0;
//	for(int i=cnt;i>=1;i--) suf[i]=suf[i+1]*i%mod;
	for(int i=1;i<=cnt;i++) {
		if(p[i]==-1) {
			p[i]=q[i]=1;
			p[i]=1ll*r1*fpow(x-X[i],mod-2)%mod;
			if(i) q[i]=pre[i-1];
			if(i<cnt) {
				q[i]=1ll*q[i]*pre[cnt-i]%mod;
				if((cnt-i)&1) q[i]=mod-q[i];
////				for(int j=i+1;j<=cnt;j++) q[i]=1ll*q[i]*(i-j)%mod;
			}
//			for(int j=1;j<=cnt;j++)
//				if(i!=j) p[i]=1ll*p[i]*(x-X[j])%mod,q[i]=1ll*q[i]*(X[i]-X[j])%mod;
			p[i]=(p[i]%mod+mod)%mod;
//			q[i]=(q[i]%mod+mod)%mod;
			q[i]=fpow(q[i],mod-2);
			q[i]=(q[i]%mod+mod)%mod;
			p[i]=1ll*p[i]*q[i]%mod;
			p[i]=(p[i]%mod+mod)%mod;
		}
//		}
//		p=(p%mod+mod)%mod; q=(q%mod+mod)%mod;
		res=ADD(res,1ll*Y[i]*p[i]%mod);
	}
	return res;
}

signed main() {
//	freopen("2.in","r",stdin);
	cin.tie(0); ios::sync_with_stdio(false);
	cin>>n; 
//	int mx=0;
	pre[0]=1; for(int i=1;i<=n+10;i++) pre[i]=1ll*pre[i-1]*i%mod;
//	pinv[0]=1; for(int i=1;i<=n;i++) pinv[i]=1ll*pinv[i-1]*fpow(i,mod-2)%mod;
//	for(int i=0;i<=M-5;i++) inv[i]=fpow(i,mod-2);
	for(int i=1;i<=n;i++) {
		cin>>a[i]>>b[i];
		lsh[++tot]=a[i]; lsh[++tot]=b[i]; 
		lsh[++tot]=max(0,a[i]-1);
//		lsh[++tot]=a[i]+1;
//		mx=max(mx,b[i]);
//		lsh[++tot]=max(0ll,b[i]-1);
		lsh[++tot]=b[i]+1;
	}
	f[0][0]=1; 
	lsh[++tot]=0; 
//	lsh[++tot]=mx+1;
//	lsh[++tot]=mx+1; lsh[++tot]=1;
	stable_sort(lsh+1,lsh+1+tot); tot=unique(lsh+1,lsh+1+tot)-lsh-1;
	for(int i=1;i<tot;i++) {
		int l=lsh[i],r=lsh[i+1]-1; //[,)
		if(r<=l+n) {
			for(int j=0;j<=n;j++) {
				if(a[j]<=l&&r<=b[j]) {
					if(j) 
						for(int k=l;k<=r;k+=4) {
							f[j][k-l]=ADD(g[j-1][k-l],sum[j-1]);
							if(k+1<=r) f[j][k-l+1]=ADD(g[j-1][k-l+1],sum[j-1]);
							if(k+2<=r) f[j][k-l+2]=ADD(g[j-1][k-l+2],sum[j-1]);
							if(k+3<=r) f[j][k-l+3]=ADD(g[j-1][k-l+3],sum[j-1]);
						}
				} else {
					if(j) 
						for(int k=l;k<=r;k+=4) {
							f[j][k-l]=f[j-1][k-l];
							if(k+1<=r) f[j][k-l+1]=f[j-1][k-l+1];
							if(k+2<=r) f[j][k-l+2]=f[j-1][k-l+2];
							if(k+3<=r) f[j][k-l+3]=f[j-1][k-l+3];
						}
				}
				for(int k=l;k<=r;k+=4) {
					g[j][k-l]=f[j][k-l];
					if(k>l) g[j][k-l]=ADD(g[j][k-l],g[j][k-1-l]);
					if(k+1<=r) {
						g[j][k-l+1]=f[j][k-l+1];
						if(k+1>l) g[j][k-l+1]=ADD(g[j][k-l+1],g[j][k-1-l+1]);
					}
					if(k+2<=r) {
						g[j][k-l+2]=f[j][k-l+2];
						if(k+2>l) g[j][k-l+2]=ADD(g[j][k-l+2],g[j][k-1-l+2]);
					}
					if(k+3<=r) {
						g[j][k-l+3]=f[j][k-l+3];
						if(k+3>l) g[j][k-l+3]=ADD(g[j][k-l+3],g[j][k-1-l+3]);
					}
				}
			}
			for(int j=0;j<=n;j++) {
				for(int k=l;k<=r;k+=4) {
					sum[j]=ADD(sum[j],f[j][k-l]);
					if(k+1<=r) sum[j]=ADD(sum[j],f[j][k-l+1]);
					if(k+2<=r) sum[j]=ADD(sum[j],f[j][k-l+2]);
					if(k+3<=r) sum[j]=ADD(sum[j],f[j][k-l+3]);
				}
			}
			for(int j=0;j<=n;j++) {
//				for(int k=0;k<=r-l;k++) f[j][k]=g[j][k]=0;
				memset(f[j],0,sizeof(int)*(r-l+1));
				memset(g[j],0,sizeof(int)*(r-l+1));
			}
//			f[0][0]=1;
		} else {
			int R=l+n;
			for(int j=0;j<=n;j++) {
				if(a[j]<=l&&R<=b[j]) {
					if(j) 
						for(int k=l;k<=R;k+=4) {
							f[j][k-l]=ADD(g[j-1][k-l],sum[j-1]);
							if(k+1<=R) f[j][k-l+1]=ADD(g[j-1][k-l+1],sum[j-1]);
							if(k+2<=R) f[j][k-l+2]=ADD(g[j-1][k-l+2],sum[j-1]);
							if(k+3<=R) f[j][k-l+3]=ADD(g[j-1][k-l+3],sum[j-1]);
						}
				} else {
					if(j) 
						for(int k=l;k<=R;k+=4) {
							f[j][k-l]=f[j-1][k-l];
							if(k+1<=R) f[j][k-l+1]=f[j-1][k-l+1];
							if(k+2<=R) f[j][k-l+2]=f[j-1][k-l+2];
							if(k+3<=R) f[j][k-l+3]=f[j-1][k-l+3];
						}
				}
				for(int k=l;k<=R;k+=4) {
					g[j][k-l]=f[j][k-l];
					if(k>l) g[j][k-l]=ADD(g[j][k-l],g[j][k-1-l]);
					if(k+1<=R) {
						g[j][k-l+1]=f[j][k-l+1];
						if(k+1>l) g[j][k-l+1]=ADD(g[j][k-l+1],g[j][k-1-l+1]);
					}
					if(k+2<=R) {
						g[j][k-l+2]=f[j][k-l+2];
						if(k+2>l) g[j][k-l+2]=ADD(g[j][k-l+2],g[j][k-1-l+2]);
					}
					if(k+3<=R) {
						g[j][k-l+3]=f[j][k-l+3];
						if(k+3>l) g[j][k-l+3]=ADD(g[j][k-l+3],g[j][k-1-l+3]);
					}
				}
			}
			for(int j=1;j<=R-l+1;j++) p[j]=q[j]=-1;
			cnt=R-l+1; r1=1;
			for(int j=1;j<=cnt;j++) X[j]=j+l-1,r1=1ll*r1*(r-X[j])%mod;
			for(int j=0;j<=n;j++) {
				for(int k=l;k<=R;k++) Y[k-l+1]=g[j][k-l];
				sum[j]=ADD(sum[j],F(r));
			}
			for(int j=0;j<=n;j++) { 
//				for(int k=0;k<=R-l;k++) f[j][k]=g[j][k]=0;
				memset(f[j],0,sizeof(int)*(R-l+1));
				memset(g[j],0,sizeof(int)*(R-l+1));
			}
//			for(int j=0;j<=n;j++) {
//				unordered_map<int,int>().swap(f[j]);
//				unordered_map<int,int>().swap(g[j]);
//			}
//			f[0][0]=1;
		}
	}
//	for(int i=0;i<=mx;i++) cout<<f[n][i]<<' ';
//	cout<<g[n][mx]-1<<'\n';
	int ans=((sum[n]-1)%mod+mod)%mod;
	cout<<ans;
	return 0; 
}
posted @ 2023-02-02 23:28  FxorG  阅读(39)  评论(0)  编辑  收藏  举报