uoj #770. 【UER #11】切割冰片

https://uoj.ac/contest/79/problem/770

赛时睡了一觉后就会转化了/hsh

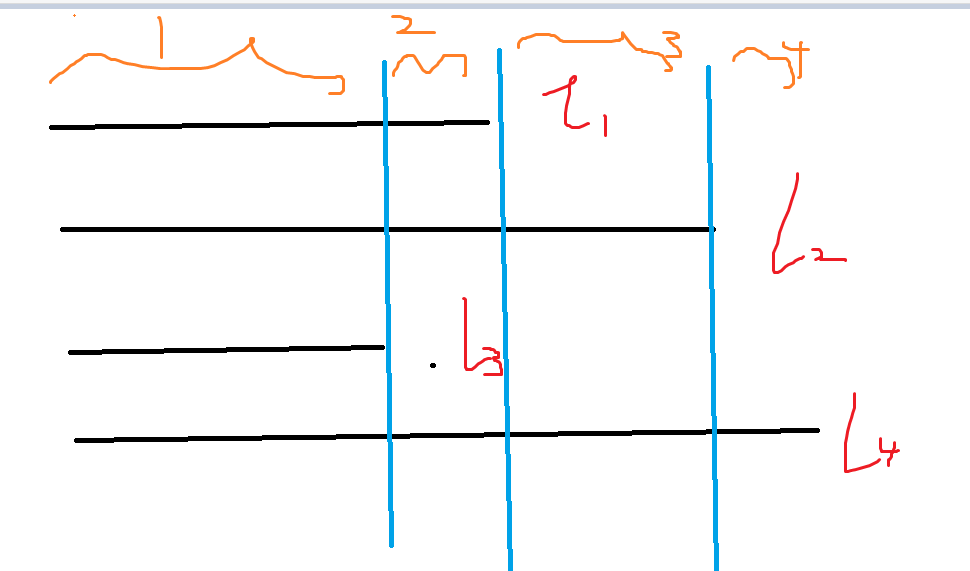
1. 考虑这个竖线倘若存在第 $i$ 条能发到 $+\infty$，那么 $i$ 之后的也一定能发到！

2. 考虑每条横线“阻挡”了一段区间的竖线发到 $+\infty$，那么横线阻挡的区间肯定不交，且它是一段一段的，也就是说，第 $i$ 条横线阻挡的区间在第 $j$ 条横线的前面，$i<j$。这个随便就能看出来了。

3. 假如你用 $n$ 条横线，覆盖了前 $j$ 条竖线，那么第 $j$ 条竖线之后的形状是一定的，因此你只要考虑前面有多少种形状即可。

4. 一种不同的覆盖方案对应一种不同的形状，显然不存在相同的覆盖方案但能覆盖出不同的形状，也不存在不同的覆盖方案但能覆盖出相同的形状。

既然如此，不妨想到 $dp(i,j)$ 表示前 $i$ 条横线，覆盖了前 $j$ 条竖线的方案数。转移的时候考虑当前这条横线做了多少次转移即可，注意需要看看是否当前横线能够覆盖得到，倘若覆盖不到的话，因为可以不覆盖，直接转移前面的即可。

60~80分记录

然后不难发现是一个前缀和选点的形式，也就是你要选若干点，单不降，且满足在其区间里，倘若不在其区间里，那么那一个只能跟上一个相等（即选空）

即问题变为，你要构造一个序列 $a$，满足 $a_i\ge a_{i-1}$，且 $a_i\le L_i$，否则，即 $a_i>L_i$，你需要满足 $a_i=a_{i-1}$，求构造序列的方案数。实际意义即为每条横线要么不覆盖，要么覆盖它能覆盖的，且覆盖区间不交，单不降。

考虑按其右端点进行划分（不存在线段覆盖了某个区间的一部分）

那么你定义 $dp(i,j)$ 为构造到第 $i$ 个位置，$a_i$ 在第 $j$ 个区间内的方案数，显然你要枚举 $k$，然后 $[k,i]$ 这部分的 $a$ 都在第 $j$ 个区间内，然后进行转移。

需要注意的是，那么你 $a_{k-1}<a_{k}$ 了，所以一定要满足 $L_k\ge R_j$，即能覆盖到第 $j$ 个区间，否则那你就只能跟上一个取等得到 $a_k$ 取当前这一个区间的值，然而你 $a_{k-1}$ 已经钦定在上一个区间了。

然后考虑组合数即可，注意对于中途不满足 $L_k\ge R_j$ 的你就让他跟上一个取等即可，也就是你现在要让满足的点形成单调不降序列。

构造双射求单调不降

然后问题变为计算一个很大的组合数作为转移系数，注意到 $n,m$ 同时加 $1$，你列一下就能 $O(1)$ 求出这东西啦。

AC记录

#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define ADD(x,y) ((x)+(y)>=mod?(x)+(y)-mod:(x)+(y))
using namespace std;
const int mod=998244353;
const int N=505;
int dp[N][N],f[N][N],n,m,L[N],inv[1002],lsh[N],tot; 

int fpow(int x,int y) {
	int res=1; x%=mod;
	while(y) {
		if(y&1) res=1ll*res*x%mod;
		y>>=1; x=1ll*x*x%mod;
	} return res;
}

signed main() {
	cin.tie(0); ios::sync_with_stdio(false);
	inv[0]=1; for(int i=1;i<=1000;i++) inv[i]=fpow(i,mod-2);
	cin>>m>>n;
	for(int i=1;i<=n;i++) {
		cin>>L[i]; L[i]=min(L[i],m);
	}
	for(int i=1;i<=n;i++) lsh[++tot]=L[i];
	sort(lsh+1,lsh+1+tot); tot=unique(lsh+1,lsh+1+tot)-lsh-1;
//	for(int v=0;v<=tot;v++) {
//		for(int i=1;i<=n;i++) {
//			int res=0; 
//			for(int j=i;j<=n;j++) {
//				if(!v) {
//					cval[v][i][j]=1; continue ;
//				}
//				if(L[j]>=lsh[v]) ++res;
//				cval[v][i][j]=C(lsh[v]-lsh[v-1]+res-1,res);
//			}
//		}
//	}
	dp[0][0]=f[0][0]=1;
	for(int i=1;i<=tot;i++) f[0][i]=ADD(f[0][i-1],dp[0][i]);
	for(int i=1;i<=n;i++) {
		dp[i][0]=1;
		for(int j=1;j<=tot;j++) {
			if(L[i]<lsh[j]) {
				for(int k=j;k<=tot;k++) dp[i][k]=dp[i-1][k];
				break ;
			}
			int res=1,nn=lsh[j]-lsh[j-1]-1,mm=0;
			for(int k=i;k>=1;k--) {
				if(L[k]<lsh[j]) continue ;
				if(L[k]>=lsh[j]) {
					++nn; ++mm; res=res*nn%mod*inv[mm]%mod;
				}
//				int qwq=C(lsh[j]-lsh[j-1]+res-1,res);
				dp[i][j]=ADD(dp[i][j],1ll*f[k-1][j-1]*res%mod);
				if(dp[i][j]<0) dp[i][j]+=mod;
			}
//			dp[i][j]=f[i-1][j];
		}
		f[i][0]=dp[i][0];
		for(int j=1;j<=tot;j++) f[i][j]=ADD(f[i][j-1],dp[i][j]);
//		for(int j=0;j<=tot;j++) cout<<dp[i][j]<<' ';
//		cout<<'\n';
	}
	int ans=0;
	for(int i=0;i<=tot;i++) {
		ans=ADD(ans,dp[n][i]);
	}
	ans=(ans%mod+mod)%mod;
	cout<<ans;
	return 0;
} 

__EOF__

本文作者：F x o r G
本文链接：https://www.cnblogs.com/xugangfan/p/16913486.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！