第三十篇 玩转数据结构——字典树（Trie）

 

 

 

1.. Trie通常被称为"字典树"或"前缀树"

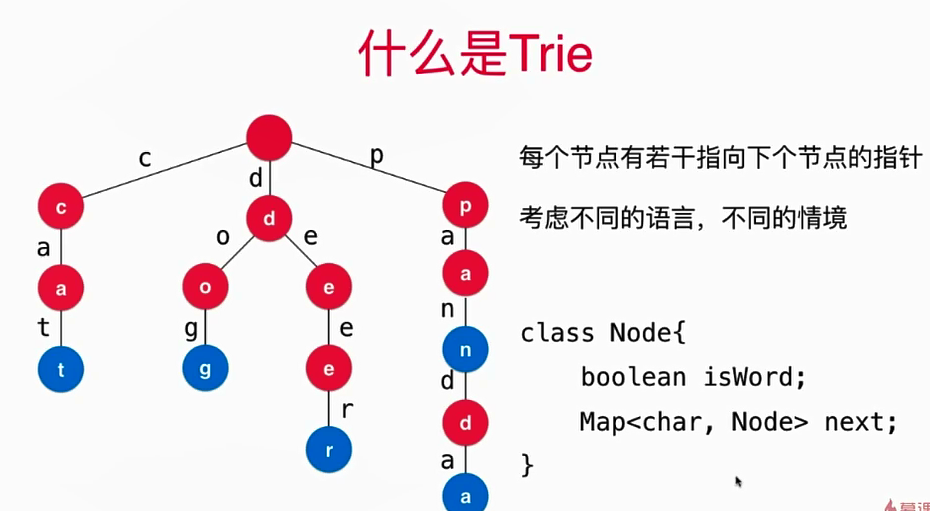
• Trie的形象化描述如下图：
• 
• Trie的优势和适用场景
• 

   

2.. 实现Trie

• 实现Trie的业务无逻辑如下：

• import java.util.TreeMap;
  
  public class Trie {
  
      private class Node {
  
          public boolean isWord;
          public TreeMap<Character, Node> next;
  
          // 构造函数
          public Node(boolean isWord) {
              this.isWord = isWord;
              next = new TreeMap<>();
          }
  
          // 无参数构造函数
          public Node() {
              this(false);
          }
      }
  
      private Node root;
      private int size;
  
      // 构造函数
      public Trie() {
          root = new Node();
          size = 0;
      }
  
      // 实现getSize方法，获得Trie中存储的单词数量
      public int getSize() {
          return size;
      }
  
      // 实现add方法，向Trie中添加新的单词word
      public void add(String word) {
  
          Node cur = root;
          for (int i = 0; i < word.length(); i++) {
              char c = word.charAt(i);
              if (cur.next.get(c) == null) {
                  cur.next.put(c, new Node());
              }
              cur = cur.next.get(c);
          }
          if (!cur.isWord) {
              cur.isWord = true;
              size++;
          }
      }
  
      // 实现contains方法，查询Trie中是否包含单词word
      public boolean contains(String word) {
  
          Node cur = root;
          for (int i = 0; i < word.length(); i++) {
              char c = word.charAt(i);
              if (cur.next.get(c) == null) {
                  return false;
              }
              cur = cur.next.get(c);
          }
          return cur.isWord;  // 好聪明
      }
  
      // 实现isPrefix方法，查询Trie中时候保存了以prefix为前缀的单词
      public boolean isPrefix(String prefix) {
  
          Node cur = root;
          for (int i = 0; i < prefix.length(); i++) {
              char c = prefix.charAt(i);
              if (cur.next.get(c) == null) {
                  return false;
              }
              cur = cur.next.get(c);
          }
          return true;
      }
  }

   

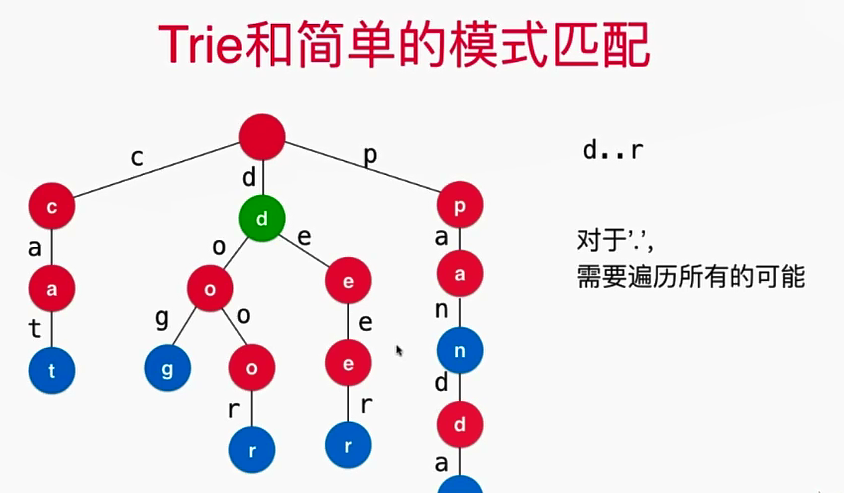
3.. Trie和简单的模式匹配

• 

   

• 实现的业务逻辑如下：

• import java.util.TreeMap;
  
  class WordDictionary {
  
      private class Node {
  
          public boolean isWord;
          public TreeMap<Character, Node> next;
  
          public Node(boolean isWord) {
              this.isWord = isWord;
              next = new TreeMap<>();
          }
  
          public Node() {
              this(false);
          }
  
      }
  
      /**
       * Initialize your data structure here.
       */
      private Node root;
  
      public WordDictionary() {
          root = new Node();
      }
  
      /**
       * Adds a word into the data structure.
       */
      public void addWord(String word) {
          Node cur = root;
          for (int i = 0; i < word.length(); i++) {
              char c = word.charAt(i);
              if (cur.next.get(c) == null) {
                  cur.next.put(c, new Node());
              }
              cur = cur.next.get(c);
          }
          cur.isWord = true;
      }
  
      /**
       * Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
       */
      public boolean search(String word) {
          return match(root, word, 0);
      }
  
      private boolean match(Node node, String word, int index) {
          if (index == word.length()) {
              return node.isWord;
          }
  
          char c = word.charAt(index);
          if (c != '.') {
              if (node.next.get(c) == null) {
                  return false;
              }
              return match(node.next.get(c), word, index + 1);
          } else {
              for (char nextChar : node.next.keySet()) {
                  if (match(node.next.get(nextChar), word, index + 1)) {
                      return true;
                  }
              }
              return false;
          }
      }
  }