判别模型、生成模型与朴素贝叶斯方法
转载时请注明来源:http://www.cnblogs.com/jerrylead
1判别模型与生成模型
上篇报告中提到的回归模型是判别模型,也就是根据特征值来求结果的概率。形式化表示为![]() ,在参数
,在参数![]() 确定的情况下,求解条件概率
确定的情况下,求解条件概率![]() 。通俗的解释为在给定特征后预测结果出现的概率。
。通俗的解释为在给定特征后预测结果出现的概率。
比如说要确定一只羊是山羊还是绵羊,用判别模型的方法是先从历史数据中学习到模型,然后通过提取这只羊的特征来预测出这只羊是山羊的概率,是绵羊的概率。换一种思路,我们可以根据山羊的特征首先学习出一个山羊模型,然后根据绵羊的特征学习出一个绵羊模型。然后从这只羊中提取特征,放到山羊模型中看概率是多少,再放到绵羊模型中看概率是多少,哪个大就是哪个。形式化表示为求![]() (也包括
(也包括![]() ,y是模型结果,x是特征。
,y是模型结果,x是特征。
利用贝叶斯公式发现两个模型的统一性:
由于我们关注的是y的离散值结果中哪个概率大(比如山羊概率和绵羊概率哪个大),而并不是关心具体的概率,因此上式改写为:
由![]() ,因此有时称判别模型求的是条件概率,生成模型求的是联合概率。
,因此有时称判别模型求的是条件概率,生成模型求的是联合概率。
常见的判别模型有线性回归、对数回归、线性判别分析、支持向量机、boosting、条件随机场、神经网络等。
常见的生产模型有隐马尔科夫模型、朴素贝叶斯模型、高斯混合模型、LDA、Restricted Boltzmann Machine等。
这篇博客较为详细地介绍了两个模型:
http://blog.sciencenet.cn/home.php?mod=space&uid=248173&do=blog&id=227964
2高斯判别分析(Gaussian discriminant analysis)
1) 多值正态分布
多变量正态分布描述的是n维随机变量的分布情况,这里的![]() 变成了向量,
变成了向量,![]() 也变成了矩阵
也变成了矩阵![]() 。写作
。写作![]() 。假设有n个随机变量X1,X2,…,Xn。
。假设有n个随机变量X1,X2,…,Xn。![]() 的第i个分量是E(Xi),而
的第i个分量是E(Xi),而![]() 。
。
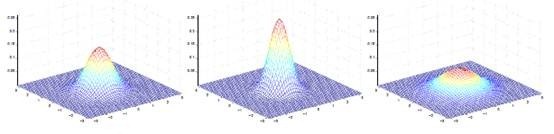
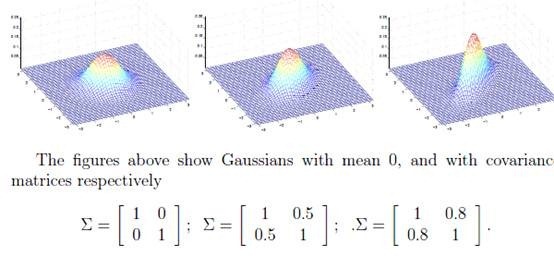
概率密度函数如下:
如下图:
2) 模型分析与应用
如果输入特征x是连续型随机变量,那么可以使用高斯判别分析模型来确定p(x|y)。
模型如下:
输出结果服从伯努利分布,在给定模型下特征符合多值高斯分布。通俗地讲,在山羊模型下,它的胡须长度,角大小,毛长度等连续型变量符合高斯分布,他们组成的特征向量符合多值高斯分布。
这样,可以给出概率密度函数:
最大似然估计如下:
注意这里的参数有两个![]() ,表示在不同的结果模型下,特征均值不同,但我们假设协方差相同。反映在图上就是不同模型中心位置不同,但形状相同。这样就可以用直线来进行分隔判别。
,表示在不同的结果模型下,特征均值不同,但我们假设协方差相同。反映在图上就是不同模型中心位置不同,但形状相同。这样就可以用直线来进行分隔判别。
求导后,得到参数估计公式:
如前面所述,在图上表示为:
直线两边的y值不同,但协方差矩阵相同,因此形状相同。![]() 不同,因此位置不同。
不同,因此位置不同。
3) 高斯判别分析(GDA)与logistic回归的关系
将GDA用条件概率方式来表述的话,如下:
进一步推导出
这个形式就是logistic回归的形式。
也就是说如果p(x|y)符合多元高斯分布,那么p(y|x)符合logistic回归模型。反之,不成立。为什么反过来不成立呢?因为GDA有着更强的假设条件和约束。
如果认定训练数据满足多元高斯分布,那么GDA能够在训练集上是最好的模型。然而,我们往往事先不知道训练数据满足什么样的分布,不能做很强的假设。Logistic回归的条件假设要弱于GDA,因此更多的时候采用logistic回归的方法。
![]() ,那么p(y|x)也是logistic回归的。这个时候如果采用GDA,那么效果会比较差,因为训练数据特征的分布不是多元高斯分布,而是泊松分布。
,那么p(y|x)也是logistic回归的。这个时候如果采用GDA,那么效果会比较差,因为训练数据特征的分布不是多元高斯分布,而是泊松分布。
这也是logistic回归用的更多的原因。
3朴素贝叶斯模型
在GDA中,我们要求特征向量x是连续实数向量。如果x是离散值的话,可以考虑采用朴素贝叶斯的分类方法。
假如要分类垃圾邮件和正常邮件。分类邮件是文本分类的一种应用。
假设采用最简单的特征描述方法,首先找一部英语词典,将里面的单词全部列出来。然后将每封邮件表示成一个向量,向量中每一维都是字典中的一个词的0/1值,1表示该词在邮件中出现,0表示未出现。
比如一封邮件中出现了“a”和“buy”,没有出现“aardvark”、“aardwolf”和“zygmurgy”,那么可以形式化表示为:
假设字典中总共有5000个词,那么x是5000维的。这时候如果要建立多项式分布模型(二项分布的扩展)。
|
多项式分布(multinomial distribution) 某随机实验如果有k个可能结局A1,A2,…,Ak,它们的概率分布分别是p1,p2,…,pk,那么在N次采样的总结果中,A1出现n1次,A2出现n2次,…,Ak出现nk次的这种事件的出现概率P有下面公式:(Xi代表出现ni次) |
对应到上面的问题上来,把每封邮件当做一次随机试验,那么结果的可能性有![]() 种。意味着pi有
种。意味着pi有![]() 个,参数太多,不可能用来建模。
个,参数太多,不可能用来建模。
换种思路,我们要求的是p(y|x),根据生成模型定义我们可以求p(x|y)和p(y)。假设x中的特征是条件独立的。这个称作朴素贝叶斯假设。如果一封邮件是垃圾邮件(y=1),且这封邮件出现词“buy”与这封邮件是否出现“price”无关,那么“buy”和“price”之间是条件独立的。
形式化表示为,(如果给定Z的情况下,X和Y条件独立):
也可以表示为:
回到问题中
这个与NLP中的n元语法模型有点类似,这里相当于unigram。
这里我们发现朴素贝叶斯假设是约束性很强的假设,“buy”从通常上讲与“price”是有关系,我们这里假设的是条件独立。(注意条件独立和独立是不一样的)
建立形式化的模型表示:
那么我们想要的是模型在训练数据上概率积能够最大,即最大似然估计如下:
注意这里是联合概率分布积最大,说明朴素贝叶斯是生成模型。
求解得:
最后一个式子是表示y=1的样本数占全部样本数的比例,前两个表示在y=1或0的样本中,特征Xj=1的比例。
然而我们要求的是
实际是求出分子即可,分母对y=1和y=0都一样。
当然,朴素贝叶斯方法可以扩展到x和y都有多个离散值的情况。对于特征是连续值的情况,我们也可以采用分段的方法来将连续值转化为离散值。具体怎么转化能够最优,我们可以采用信息增益的度量方法来确定(参见Mitchell的《机器学习》决策树那一章)。
比如房子大小可以如下划分成离散值:
4拉普拉斯平滑
朴素贝叶斯方法有个致命的缺点就是对数据稀疏问题过于敏感。
比如前面提到的邮件分类,现在新来了一封邮件,邮件标题是“NIPS call for papers”。我们使用更大的网络词典(词的数目由5000变为35000)来分类,假设NIPS这个词在字典中的位置是35000。然而NIPS这个词没有在训练数据中出现过,这封邮件第一次出现了NIPS。那我们算概率的时候如下:
由于NIPS在以前的不管是垃圾邮件还是正常邮件都没出现过,那么结果只能是0了。
显然最终的条件概率也是0。
原因就是我们的特征概率条件独立,使用的是相乘的方式来得到结果。
为了解决这个问题,我们打算给未出现特征值,赋予一个“小”的值而不是0。
具体平滑方法如下:
假设离散型随机变量z有{1,2,…,k}个值,我们用![]() 来表示每个值的概率。假设有m个训练样本中,z的观察值是
来表示每个值的概率。假设有m个训练样本中,z的观察值是![]() 其中每一个观察值对应k个值中的一个。那么根据原来的估计方法可以得到
其中每一个观察值对应k个值中的一个。那么根据原来的估计方法可以得到
说白了就是z=j出现的比例。
拉普拉斯平滑法将每个k值出现次数事先都加1,通俗讲就是假设他们都出现过一次。
那么修改后的表达式为:
这个有点像NLP里面的加一平滑法,当然还有n多平滑法了,这里不再详述。
回到邮件分类的问题,修改后的公式为:
5文本分类的事件模型
回想一下我们刚刚使用的用于文本分类的朴素贝叶斯模型,这个模型称作多值伯努利事件模型(multi-variate Bernoulli event model)。在这个模型中,我们首先随机选定了邮件的类型(垃圾或者普通邮件,也就是p(y)),然后一个人翻阅词典,从第一个词到最后一个词,随机决定一个词是否要在邮件中出现,出现标示为1,否则标示为0。然后将出现的词组成一封邮件。决定一个词是否出现依照概率p(xi|y)。那么这封邮件的概率可以标示为![]() 。
。
让我们换一个思路,这次我们不先从词典入手,而是选择从邮件入手。让i表示邮件中的第i个词,xi表示这个词在字典中的位置,那么xi取值范围为{1,2,…|V|},|V|是字典中词的数目。这样一封邮件可以表示成![]() ,n可以变化,因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个,这样就形成了一封邮件。这相当于重复投掷|V|面的骰子,将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y),而且每次试验条件独立。这样我们得到的邮件概率是
,n可以变化,因为每封邮件的词的个数不同。然后我们对于每个xi随机从|V|个值中取一个,这样就形成了一封邮件。这相当于重复投掷|V|面的骰子,将观察值记录下来就形成了一封邮件。当然每个面的概率服从p(xi|y),而且每次试验条件独立。这样我们得到的邮件概率是![]() 。居然跟上面的一样,那么不同点在哪呢?注意第一个的n是字典中的全部的词,下面这个n是邮件中的词个数。上面xi表示一个词是否出现,只有0和1两个值,两者概率和为1。下面的xi表示|V|中的一个值,|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值,下面的x的向量都是字典中的位置。
。居然跟上面的一样,那么不同点在哪呢?注意第一个的n是字典中的全部的词,下面这个n是邮件中的词个数。上面xi表示一个词是否出现,只有0和1两个值,两者概率和为1。下面的xi表示|V|中的一个值,|V|个p(xi|y)相加和为1。是多值二项分布模型。上面的x向量都是0/1值,下面的x的向量都是字典中的位置。
形式化表示为:
那么我们仍然按照朴素贝叶斯的方法求得最大似然估计概率为
解得,
与以前的式子相比,分母多了个ni,分子由0/1变成了k。
举个例子:
|
X1 |
X2 |
X3 |
Y |
|
1 |
2 |
- |
1 |
|
2 |
1 |
- |
0 |
|
1 |
3 |
2 |
0 |
|
3 |
3 |
3 |
1 |
假如邮件中只有a,b,c这三词,他们在词典的位置分别是1,2,3,前两封邮件都只有2个词,后两封有3个词。
Y=1是垃圾邮件。
那么,
假如新来一封邮件为b,c那么特征表示为{2,3}。
那么
那么该邮件是垃圾邮件概率是0.6。
注意这个公式与朴素贝叶斯的不同在于这里针对整体样本求的![]() ,而朴素贝叶斯里面针对每个特征求的
,而朴素贝叶斯里面针对每个特征求的![]() ,而且这里的特征值维度是参差不齐的。
,而且这里的特征值维度是参差不齐的。
这里如果假如拉普拉斯平滑,得到公式为:
表示每个k值至少发生过一次。
另外朴素贝叶斯虽然有时候不是最好的分类方法,但它简单有效,而且速度快。

![clip_image011[8] clip_image011[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052258388155.png)
![clip_image001[4] clip_image001[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052258396419.png)
![clip_image018[28] clip_image018[28]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052258476117.png)
![clip_image025[6] clip_image025[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259044957.png)
![clip_image026[8] clip_image026[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259053363.png)
![clip_image027[8] clip_image027[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259066611.png)
![clip_image028[4] clip_image028[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/20110305225909982.png)
![clip_image035[8] clip_image035[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259177615.png)
![clip_image038[4] clip_image038[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259216172.png)
![clip_image044[8] clip_image044[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259257662.png)
![clip_image045[6] clip_image045[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259275512.png)
![clip_image052[8] clip_image052[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259320.png)

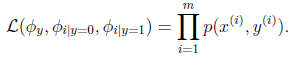
![clip_image060[8] clip_image060[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259363508.png)
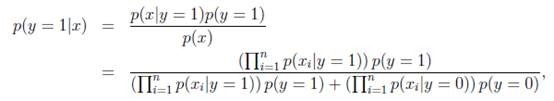
![clip_image065[8] clip_image065[8]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/20110305225939320.png)
![clip_image066[4] clip_image066[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259405761.png)
![clip_image070[4] clip_image070[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259435497.png)
![clip_image071[4] clip_image071[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/20110305225943415.png)
![clip_image073[4] clip_image073[4]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259451612.png)
![clip_image081[6] clip_image081[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259512064.png)
![clip_image082[6] clip_image082[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259544657.png)
![clip_image084[6] clip_image084[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259542083.png)

![clip_image088[6] clip_image088[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259561635.png)
![clip_image090[6] clip_image090[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259565996.png)
![clip_image097[6] clip_image097[6]](https://images.cnblogs.com/cnblogs_com/jerrylead/201103/201103052259596538.png)

