优化算法-牛顿法

牛顿法（英语：Newton's method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。

一般情况对于f(x)是一元二次的情况直接应用求根公式就可以了，但是对于更高次（在5次方以上），没有求根公式，于是牛顿想了个近似求解的办法——牛顿法

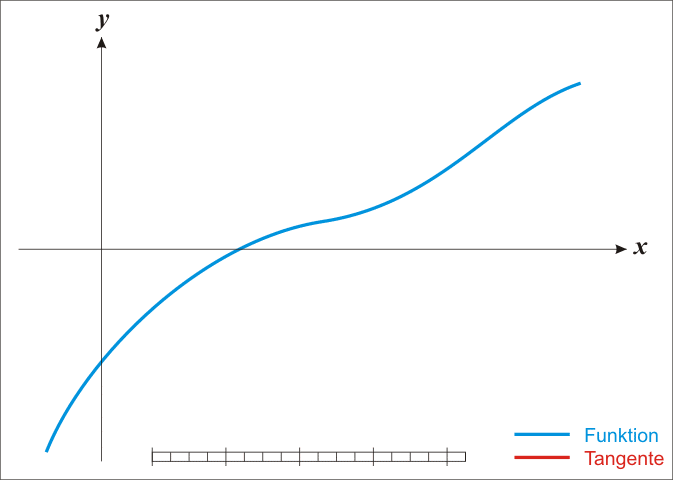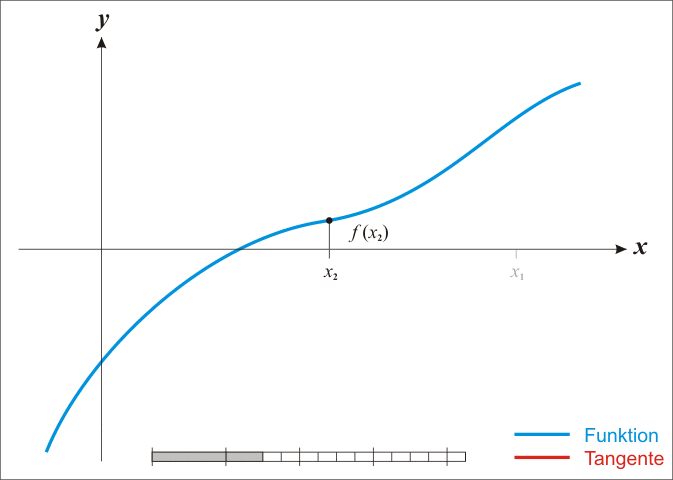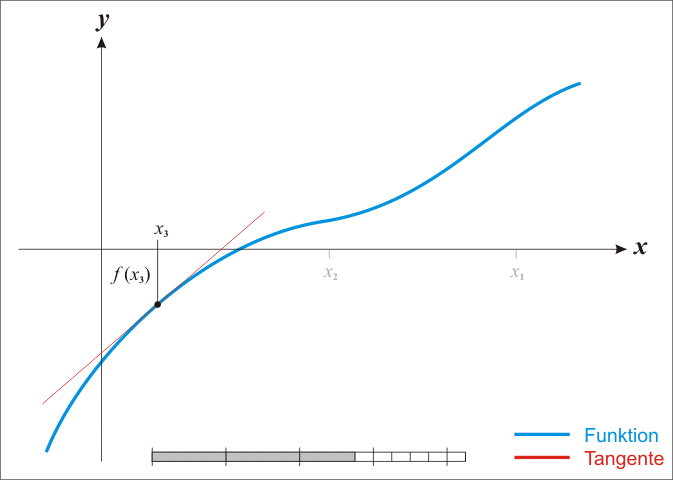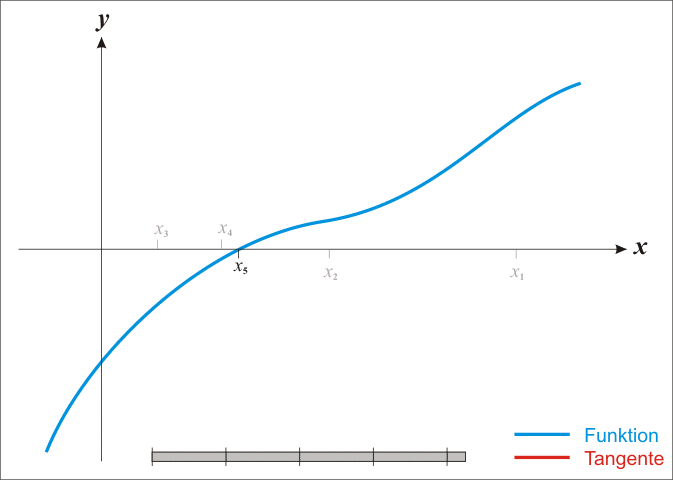
首先以一元函数为例来说明牛顿法的具体过程

假设我们要求解函数f(x)=0的根，我们首先把函数在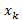处展开成泰勒级数的形式并取其线性部分：

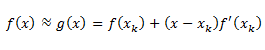
令g(x)=0，则

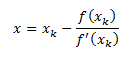
g(x)=0的根与f(x)=0的根近似相等，所以我们可以将此次计算看做一次迭代的过程，即：

 

 

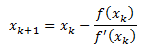
看下面的定理：

设f(x)在[a,b]满足

(1) f(a)·f(b)<0

(2) f(x)∈[a,b]，f′(x),f″(x)均存在，且f′(x)与f″( x)的符号均保持不变。

(3) f(x)·f″(x)>0, x∈[a,b] 则方程f(x)=0在[a,b]上有且只有一个实根，由牛顿法迭代公式计算得到的近似解序列收敛于方程 f(x)=0 的根 x*。

 

通俗的说，如果f(x)及其一阶、二阶导是连续的，并且待求的零点是孤立的，那么在零点周围存在一个区域，只要初始值位于这个邻近区域内，那么牛顿法必定收敛。

下面动图形象演示了牛顿法收敛过程

1. 

关于牛顿法和梯度下降法的效率对比：

　　从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

牛顿法应用f(x)求极值的问题中就是将求f(x)的极值可以转化为求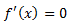的解，这时我们会用到f(x)泰勒展开式中的二阶偏导数，对于多元函数，其泰勒展开式中的二阶项可以写成如下形式：

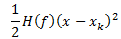
其中H(f)是海森矩阵，其形式为

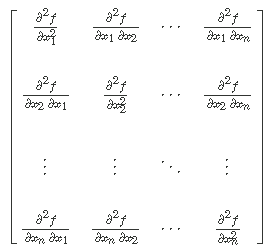
假设我们要求解f(x)在多元条件下的极值

首先需要求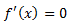

f(x)在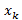处的包含二阶项的泰勒展开式（省去高阶无穷小）为

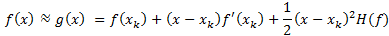
令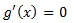可得：

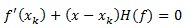
解得

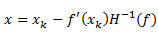
所以多元函数的梯度更新公式

牛顿法的优缺点总结：

　　优点：二阶收敛，收敛速度快；

　　缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。