POJ 2663 Tri Tiling 矩阵快速幂 难度:3
Tri Tiling
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 7841 | Accepted: 4113 |
Description
In how many ways can you tile a 3xn rectangle with 2x1 dominoes?
Here is a sample tiling of a 3x12 rectangle.
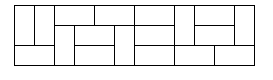
Here is a sample tiling of a 3x12 rectangle.

Input
Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 <= n <= 30.
Output
For each test case, output one integer number giving the number of possible tilings.
Sample Input
2 8 12 -1
Sample Output
3 153 2131
思路:只有八种转移状态,设初始状态为0(全空),得到状态7(111全染)
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
typedef vector<long long > vec;
typedef vector<vec> mat;
const int mod=(1<<31-1);
mat mul(mat &A,mat &B){
mat C(A.size(),vec(B[0].size()));
for(int i=0;i<A.size();i++){
for(int k=0;k<B.size();k++){
for(int j=0;j<B[0].size();j++){
C[i][j]=(C[i][j]+A[i][k]*B[k][j])%mod;
}
}
}
return C;
}
mat pow(mat A,long long n){
mat B(A.size(),vec(A.size()));
for(int i=0;i<A.size();i++){
B[i][i]=1;
}
while(n>0){
if(n&1)B=mul(B,A);
A=mul(A,A);
n>>=1;
}
return B;
}
void calc(int m){
mat m1(8,vec(8,0)),E(8,vec(8,0));
E[0][7]=1;
E[1][6]=1;
E[2][5]=1;
E[3][4]=1;
E[4][3]=1;E[4][7]=1;
E[5][2]=1;
E[6][1]=E[6][7]=1;
E[7][0]=1;E[7][4]=E[7][6]=1;
E=pow(E,m);
/*for(int i=0;i<E[0].size();i++){
for(int j=0;j<E.size();j++){
printf("%d ",E[i][j]);
}
puts("");
}*/
printf("%I64d\n",E[0][7]);
}
int main(){
int m=0;
while(scanf("%d",&m)==1&&m!=-1){
calc(m+1);
}
return 0;
}



