Proj. Unknown: Deciding Differential Privacy of Online Algorithms with Multiple Variables
Paper
https://arxiv.org/abs/2309.06615
Abstract
背景:
- 自动机A被称作查分隐私自动机:当对某些D,对任何隐私预算ε>0,该自动机是Dε-differentially private( A DiP automaton is a parametric automaton whose behavior depends on the privacy budget 𝜖. An automaton A will be said to be differentially private if, for some 𝔇, the automaton is 𝔇𝜖-differentially private for all values of 𝜖 > 0)
本文:Dip automata(DipA)
对象:处理输入流,并且会为每个输入都产生某种输出的在线算法
方法:
- 定义名为Dip Automata的自动机来描述这类允许多个实值存储量的算法(allowing multiple real-valued storage variable)
- Dip automaton是一类行为依据于隐私预算privacy budget ε的参数自动机
- 基于精度特征定义一类差分隐私Dip自动机(Q:还是所有差分隐私Dip自动机,We show that the problem of determining if a given DiP automaton belongs to this class is PSPACE-complete.),证明判定给定的Dip自动机是否属于这类差分隐私Dip自动机的问题为PSPACE-Complete。
- 本文中提到的PSPACE-Complete算法也能够计算差分隐私Dip自动机的D值
实验:证明算法确实有效
1. Intro
P1: 检测differential privacy一般来说被认为是general undecidable
P2:
定义online algo:
处理由某个分布采样得到的有限(finite)无界(unbound)输入序列,并且对每个输入都产生输出
输入:a sequence of real numbers that are answers to queries for database
Q: 为何不是query而是answer?
A: 可能是因为是在检测online algo回答的过程中(将answer转化为真正的feedback)的过程中的隐私泄露问题
重要参考文献[10]:On Linear Time Decidability of Differential Privacy for Programs with Unbounded Inputs,同一个作者
Task: 在线性时间内使用automaton来检查differential privacy
缺陷:仅仅允许单个storage variable
本文在此基础上进行拓展,允许多个storage variables
P3-:Contributions
- 拓宽了【10】的研究,允许多个real-valued storage variables
- DiPA, well-formed
- 定义: DiPA(DiP automaton): a parametric automaton(depending on privacy budget ε) with finitely many control states that process an unbounded but finite stream of real values that represent answers to queries asked of a database; DiPA can store finite real-valued varaibles
- where real values are sampled from Laplace distributions, the mean of this distribution may depend on the value read(Q)
- 这些存储值depend on input read
- transition based on: 1. the current control state 2. the value stored so far 3. the input value
- output: 属于某个有限符号集中的符号,或者是一个real number
- 定义问题:Given a DiPA A, determine whether A is Dε-differentially private for some constant D >0 and any ε > 0
- 本文(以及[10])认为可以将检查Dε-differentially private的问题视作图论问题,检查图上是否具有某些性质,例如是否存在特定的paths, cycles和iterations。
- 与[10]不同:不能只考虑the underlying graph of the automaton,需要使用auxillary graph
- Q: We use an auxiliary graph to capture those undesirable paths and cycles precisely.
- 定义-Well-formed: An automaton A is well-formed if it does not have any undesirable paths or cycles
- 性质:本文证明了:
- A well-formed DiPA is differentially private
- 如果DiPA满足条件,对A的所有state,从该state出发的transitions(总有?)不同outputs,则well-formedness是保证differential privacy的条件
- Q: DiPA + well-formed->differentially private
- Q: DiPA + Any state have distinct outpus, then if not well formed->not differentially private
- present a PSPACE algo to checks if a DiPA A is well-formed,能计算D. 本文在附录中证明了算法是PSPACE的(P∈NP∈PH∈PSPACE,图灵机可以使用多项式空间能解决的所有决策问题的集合,a strict superset of the set of context-sensitive language)
- 工具DiPAut
- 效果:成功恒明了differetial privacy并发现了违反保密的实例
- 实验2:验证scalability
- 尽管时间性能是PSPACE的,但是速度在实际例子上还行
- 实验3:
- Competitor: CheckDP
- 效果:outperforms
2. Preliminaries
Differential Privacy: 允许对数据库的静态分析,同时确保分析结果不会泄露隐私
在Differential Privacy Framework中:
Differential Mechanism M: 一个随机算法,用来监控数据库的answer, provides privacy at the cost of accuracy
Data Analyst: 负责问queries,可能不可信,可能是攻击者
database D: 负责回复问题
Queries: 确定性问题,并且通常包含aggregate functions
Answer: 从数据库的精确回答和随机分布中根据privacy budget取得的,在DP机制下通常是noisy answer
individual: 参与调查,给数据库提供信息的主题。
令D{i}为去除了individual i贡献的信息的数据库D,则M应当保证,
对任意i∈D,对任意output vector \(\vec{o}\),\(P(\vec{o}|\sigma, D) \approx P(\vec{o}|\sigma, D\setminus \{i\})\), where σ是answers to queries
Q: those queries are 1-sensitive,为何能确定budget=1?
https://medium.com/@shaistha24/global-vs-local-differential-privacy-56b45eb22168
Gap
Sensitivity
用于将需要添加的noise总量参数化,对应单个调查参与者individual对结果变化的最大幅度
Q: 一般而言,敏感性是指基础数据集的变化对结果的影响--不明白原文这句话为何不是扰动对结果的影响,而且这里也不是在介绍local sensitivity??

这里D1和D2要求是neighbors,即d(D1,D2)≤1,这里d(x,x')是距离函数。
常用的距离函数\(d(x, x') = |x-x'∪x'-x|\),因此,增删一个元素,距离都是1,如果修改一个元素,距离则是2,因此不算在neighbors中(也有其他距离定义,这种情况下修改一个元素距离是1.Q: bounded differential privacy?)
Global Sensitivity
the max difference of the output a query function can result in when one change is made to any dataset.
For any 2 neighboring dataset D1 and D2, the answer difference between D1 and D2 is at most GS(f).
nose代表为了满足ε-DP requirements所需的噪音等级
global sensitivity基于符号集上所有数据集,因此global sensitivity更依赖于query而非数据集,在特定范围上应用范围极广
例如,对于sum操作,global sensitivity 趋近于正无穷,因为新加入的element绝对值可以趋近于正无穷。
Q: However, the global sensitivity does not exclude the possibility to generate accurate information for sum.??难道不是说global sensitivity并不好?
可以使用数据集的bounds来使得global sensitivity重新有效
Q: Global sensitivity is the min sensitivity needed for a query to cover all possible datasets???为何不是最大
对类似sum, count之类的query functions, local sensitivity与global sensitivity类似,但是对median, local sensitivity更小。
Local Sensitivity
覆盖特定数据集所需的最低敏感度Q:为何还是最低?
D1: the known dataset
Pros:这允许对一些global sensitivity难以限制的函数设置bound
Cons: 但是,如果分析者知道特定数据集查询的Local Sensitivity,则可能推断出有关数据集的某些信息,因此Q:不能用局部敏感度实现Differential Privacy
Q: 仅需n个查询就可以确定噪声规模,用来推断局部敏感度
Differential Privacy
Differential Privacy is a system for publicly sharing information about a dataset by describing the patterns of groups within dataset while withholding information about individual in the dataset.
DP更接近与一种framework而非一个算法
例子:让individual在报身高之前添加从特定分布中随机去除的噪声,从而获取某个群体的身高平均值
随机化机制的部分行为以提供隐私
差分隐私提供了什么:
an individual's expected future utility won't be harmed by more than exp(epsilon)约等于1+epsilon factors
承诺个人信息的录入不会带来更多风险,但是与security不同,不能确保在数据库上不被泄露,只能保证拦截差分攻击的概率,让攻击者无法推测个人是否在接受调查
依据:大数定律,很难分辨机器学习模型的哪些行为来自随机性,哪些来自训练数据。
但:
- 不能保证给定样本,尤其是小样本能真实反映总体特征
- 不能保证远离真实特征的样本能被后续样本所平衡
Global Differential Privacy
噪音仅仅在输出答案时添加,低budget,但是每个用户必须足够信任管理者
Local Differential Privacy
每个人自行添加噪音,高budget
Privacy Budget
数据库x的查询与数据库y上同一查询之间的最大距离,每个人可接受的隐私泄露的度
更小的隐私预算对应更强的隐私保证。多个查询常常sharing budget,以保证查询整体DP
对(ε)-Differential Privacy(又称(ε,0)-Differential Privacy)来说,
若ε较小,表现的性质基本相似
若ε较大,但有可能x,y不太可能发生在真实世界中(Q:导致噪声太小,无法保证privacy?)。攻击者可能没有足够的信息
Q:
根据ε,有两种数据库分类:
ε=0,the output of a query for all parallel databases as full database is the same value
ε=1,max distance between all the queries would be 1
机器学习中的大多数计算都可以提供differential privacy guarantee和utility guarantee
(ε, δ)-Differential Privacy

δ:信息意外泄露的概率
对所有相邻的数据库x,y,隐私泄露的绝对值将受到ε的限制,概率则为1-δ
如果δ=0,则称(ε)-Differential Privacy(又称(ε,0)-Differential Privacy)
一般而言,δ取数据库size的某个多项式度量的倒数
δ正比于\(\frac{1}{||D||}\),这种取值是非常危险的,因为随着数据库大小的增加,数据泄露的风险增长的较快
Laplace机制
利用Laplace分布作为噪声扰动每个坐标
\(F(x) = f(x) + Lap(\frac{s}{\epsilon})\)
where s is the sensitivity of f,
基于:more sensitive the query, the stronger the desired guarantee, the more noise is needed
注意,Laplace分布是对称的,而作为噪声的一般都会有这种特性
scale b 正比于 sensitivity of f(query) \ ε,而δ=0.
Q:一般b可以直接取1\ε??
在实际实现中,要额外注意浮点数等编程实现,否则可能破坏差分隐私,尤其要注意舍入,比如,在x上非零概率,在y上零概率
缺点:Laplace机制只适应于低敏感度,纯数字的查询。
Q: 对大量查询,需要更大的epsilon值。
例如,输入是一个训练数据集,输出是一个能够最小化训练误差的神经网络,如果使用Laplace机制,则会直接在神经网络权重上添加噪声,损坏神经网络训练效果。
Exponential Mechanism
analyst giving a scoring function that outputs a score, 而指数机制则要按照一定概率返回并非打分最高的元素。
Given a parameter ε, an input x, and a utility function u with generalized sensitivity Δu, the Exponential Mechanism draws an output from distribution:
\(Pr[o] = e^{\frac{\epsilon u(x,o)}{2 \Delta u}}\)
优点:无论R(值域)的大小如何,其privacy budget仅为ε;拓展性好,理论上可以适用于无限集合(但是实际上实现麻烦);总是输出合法值;
缺点:分析scoring function的敏感度很可能破译差分隐私;难以实现,具体实现常需要更宽松下界,因此常被用来证明理论下界,但是算法尝试用其他方法,尤其是Laplace方法来实现复制该机制
Gaussian Mechanism
不满足ε-DP,但是满足(ε, δ)-DP
\(F(x) = f(x) + N(\sigma^2), where \sigma^2=\frac{2 s^2 log(\frac{1.25}{\delta})}{\epsilon^2}\)
更宽松,更不准确,但是在vector-valued时,因为可以使用L1或者L2距离,因此针对L2敏感度远低于L1敏感度的应用更好
vector-valued Laplace Mechanism:
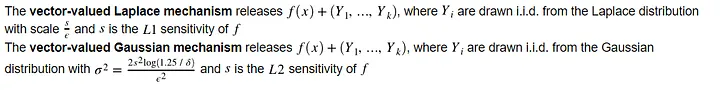
vector-valued Gaussian Mechanism:
Linking Attacks
使用auxiliary data and de-identified data来识别个人
两个数据点就足以识别大数据库中的绝大部分individuals
Q: 文中表示大部分aggregate function可以将敏感度设置为1:If queries are aggregate queries, then answers to 𝑞 on 𝐷 and 𝐷 \ {𝑖} (for individual 𝑖) are likely to be away by at most 1.
但是对于最常见的操作sum,感觉这根本不可能?
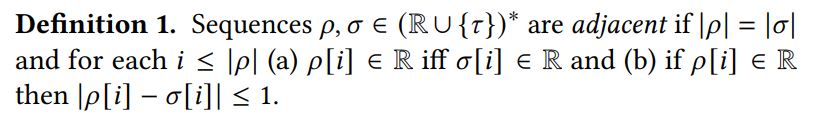

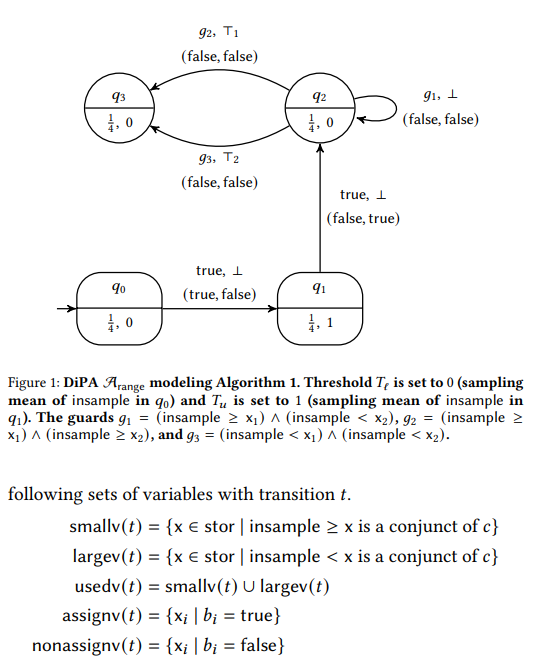
例子:algorithm 1, ε-differentially private

注意文中的Lap是Lap(d, μ)而不是Lap(μ,d),和其他教材的记述顺序相反
3. DIPA
3.1 Syntax
特点:能记住有限个control states,并有有限个real-valued variable x1,...,xk
自动机每一步都会从Laplace分布中抽取两个real values,命名为insample和insample'并存储
Steps:
- 从Lap(dε, μ)和Lap(dε', μ')中分别抽取1个real value,存储在insample和insample'中。此处d, d', μ, μ'都依赖于当前状态
- 自动机状态氛围input states和non-input states。在non-input state,自动机期待读到τ,也就是空输入标识。在input state,自动机期待读到一个实数a。自动机令insample+=a, insample'+=a。(分别对应Laplace(dε, μ+a)和Laplace(d'ε, μ' + a)
- 执行transition,更改control states并输出一个value,这个value可能是从某个有限集合中抽取的符号,也可能是insample或者insample'对于input state,会有一个比较insample和stored values xi的布尔条件,如果条件不失败则可能出发计算终止,不会执行transition
- 自动机可能将insample存入任何variable xi(1<=i<=k)



例子2将例子1化为graph形式