Proj THUDBFuzz Paper Reading: 南京大学软件分析课程2020, 05 Data Flow Analysis - Foundations I
Iterative algo, Another View
Old View:

New View:
每次迭代都是状态映射,直到迭代到状态不变为止

如果令\(X_i\)为第i步的状态\((v^i_1, v^i_2, ..., v^i_n)\),映射函数为\(F: V^k->V^k\),则\(X_{i+1}=F(x_i)\)。称满足\(X=F(X)\)的状态X为F的不动点fixed point。
尝试回答以下问题:
- 算法是否能保证终止?是否总有解?
- 是否存在多解?如果存在多解,算法是否能收敛到最好的那个?
- 收敛所需的时间复杂度?
Partial Order



Upper and Lower Bounds


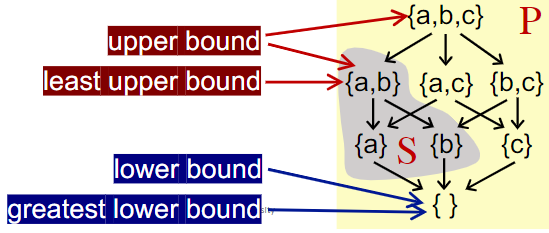
并不是全部偏序集poset都有最小上界或者最大下界,但如果有最小上界或者最大下界,对应的值一定是唯一的。

Lattice, Semilattice, Complete & Product
格
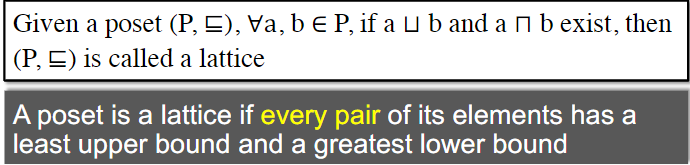
首先,肯定存在一个a∩b是{a,b}的下界,对满足z≤a和z≤b的任意z,应该有z≤a∩b,所以a∩b是最大下界。同理有最小上界。
http://math.hawaii.edu/~jb/math618/os2uh_17.pdf



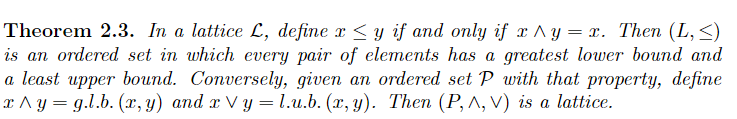
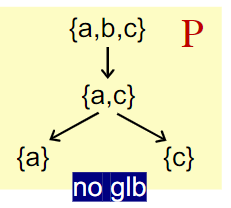
示例:
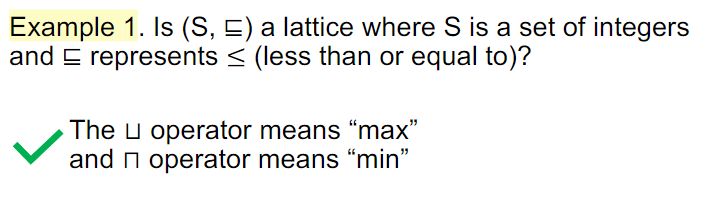


半格

所以格是join+meet半格
完全格

注意格只要求一对元素组成的集合有lub和glb,完全格则要求任意子集都要有。思考的时候很容易把格要求成完全格,比如Example1

注意这里的lub和glb可以在格内而不在挑出来的集合内

完全格上有极大元和极小元。

Every finite lattice(P is finite) is a complete lattice
注意这里已经首先是个格,所以已经满足了一对元素都有lub和glb。当P有限的时候,这些lub和glb中一定分别有一个是最终的极大元和极小元。
注意极大元不一定是least upper bound。极小元也不一定是greatest lower bound
积格

格之积还是格,完全格之积还是完全格
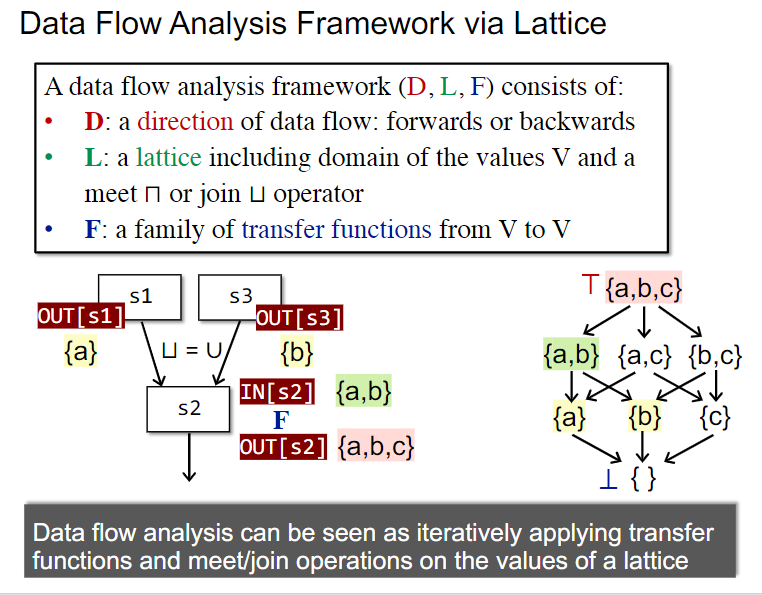
Data Flow Analysis Framework via Lattice
以格的视角重新定义一遍Data Flow Analysis Framework
尝试回答以下问题:
- 算法是否能保证终止?是否总有解?
- 在之前的表达式有效性分析等例子中,因为状态总是更高,所以能够保证终止。
- 单调性
- 但是否总有解-总有不动点?
- 是否存在多解?如果存在多解,算法是否能收敛到最好的那个?
- 想到不动点定理,明显,在不动点这里算法会收敛
- 明显可能有多解
- 但能否收敛到最好的那个?
- 收敛所需的时间复杂度?
Monotonicity and fixed point Theorem


回答了是否有解的问题

回答了是否总能收敛到最好的结果
Relate Iterative Algo to Fixed Pointed Theorem
现在需要证明transfer function + join function这一套合起来是单调的函数

如果采用transfer function f(data) = (data - KILL) + GEN,并且KILL,GEN本身不随着当前节点的data变化,只与当前节点本身有关,那么transfer function无疑是单调的。
以join为例,此时应该是从最小元开始迭代,求least fixed point。那么只要证明join操作是单调递增的即可。
设x≤y,那么,对任意z属于同个lattice,明显y≤y∪z,而x≤y,所以x≤y∪z。又因为根据∪的定义,x∪z是x和z的least upper bound(虽然可以理解,但是感觉形式证明不够充分),而y∪z是upper bound,所以有x∪z≤y∪z。

最后一个问题:何时会收敛?
这里引入新概念:格的高度。明显,每次迭代格的高度都会递增/递减。所以,最大迭代次数等于格的高度加1.
注意每次迭代都要把全部nodes更新一遍,所以时间复杂度(#nodes * height)

May/Must Analysis, A lattice View
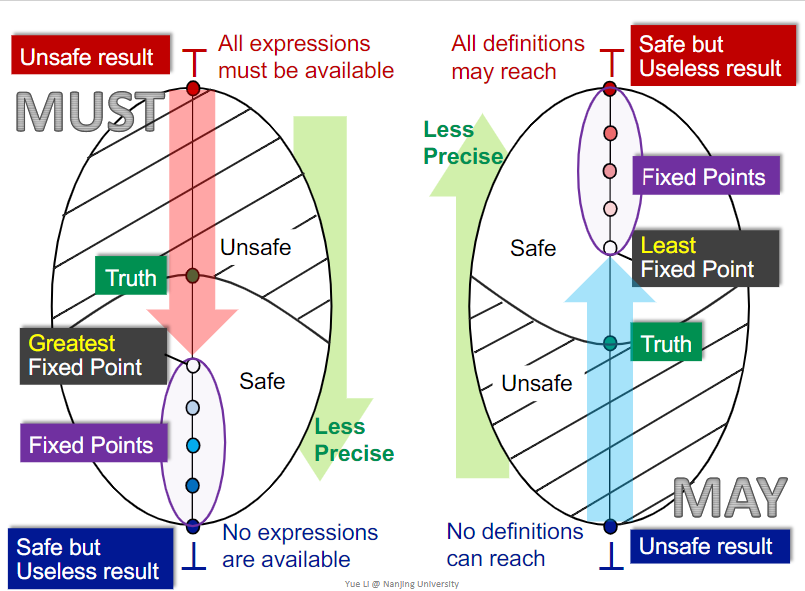
MOP and Distributivity
具体来说,Data flow analysis lattice框架最多能达到什么样的精度?
这里就必须首先引入一种meet框架:MOP: Meet-Over-All-Paths
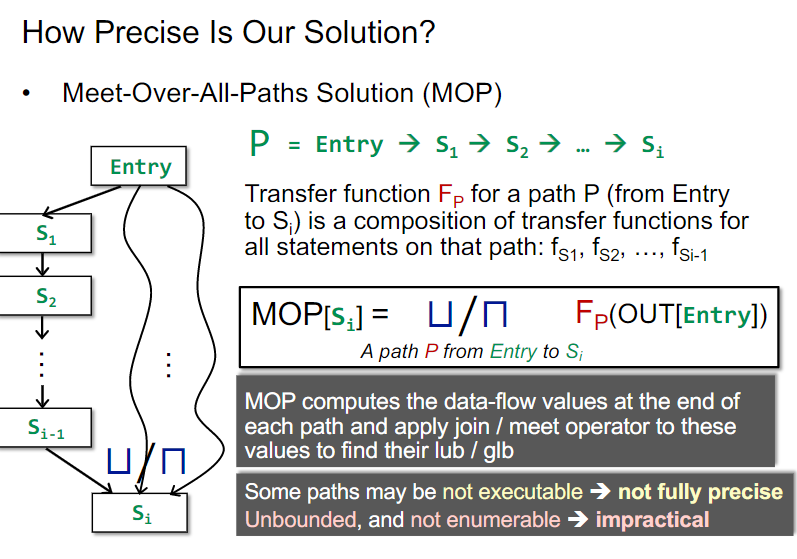
和之前例子中的方法不同的是,MOP框架每个节点记录的具体数据是对全部Entry到当前节点的路径,取其transfer functions组合变换之后的结果来做meet。与之对比,之前的例子都直接在程序交汇点先做meet了。
比如之前的方案是F(x∪y)现在的就是F(x)∪F(y),这里F是transfer functions组合。课件中称在交汇点先做meet的方法为Ours。
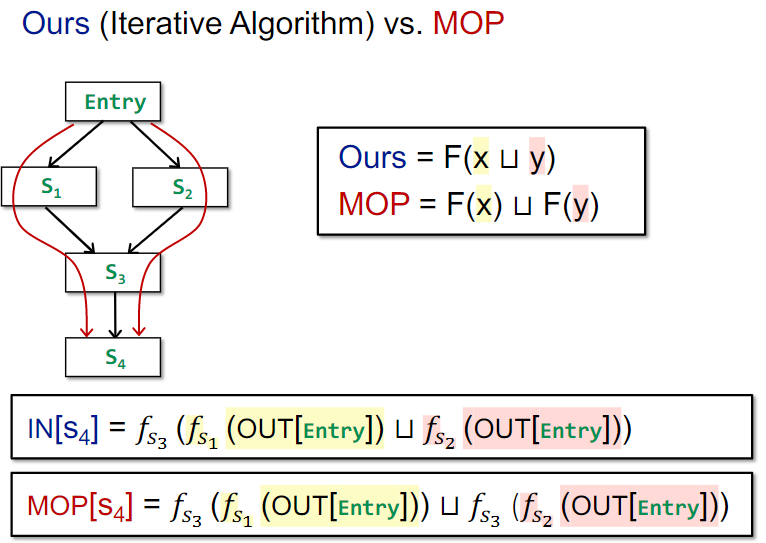
这就引出了一些问题:
- 程序点之间能否相互利用状态?还是可以的,程序点i可以利用程序点i-1的对全部Entry到当前节点的路径,取其transfer functions组合变换之后的结果状态来简化运算。
- 如何处理环?课件中认为是几乎做不到的。
此外,MOP框架还是存在有些路径实际上不可达,但是静态分析很难判断的问题,也就是说,还是会因为无效路径引入误差。
接下来证明,Ours方案比MOP方案更加不精确

不过,当F is distributive,即F(x∩y) = F(x)∩f(y)时,二者等价。

而Bit-Vector或者Gen/Kill的Meet操作恰好就是distributive的。
Constant Propagation
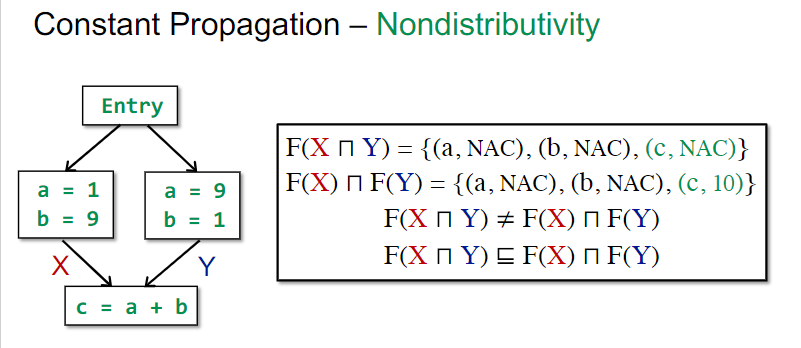
Nondistributivity的例子
问题:给定变量x和程序点p,确定x是否在p点一定是对应常量。
这里我以为像之前的表达式可达分析之类的一样以集合来做就行了,不过课件上并不是这种思路。这是因为当x同时有可能是两个常量,比如1和2时,x在p点对应非常量。由此,必须要记录所有变量的所有潜在状态。
接着我认为格应该只有undef, 变量,程序中出现的具体常量三类情况,这里课件定义了这样的一个格,引入undef和nac两种状态,分别作为最大元和最小元。
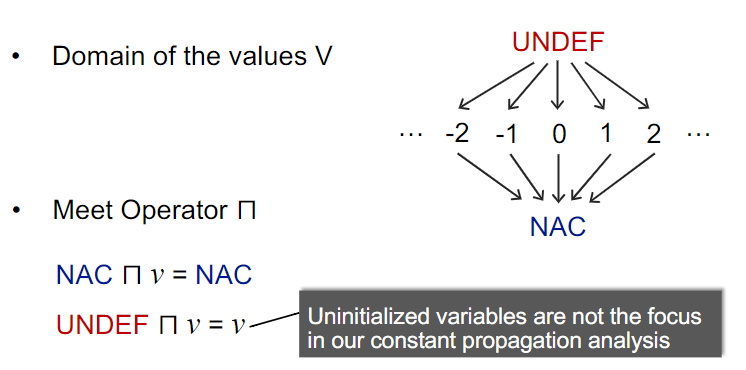
在交汇操作(meet)上,我认为对于两个具体常数,应有ca∩cb=NAC,课件满足判断。
在transfer function上,很明显还是可以加上当前定义的常量x,减去当前x的其他量。注意赋值函数可以将常数数值由一个变量传给另一个变量。

Q:为何f(y,z)有可能成为undef,难道不是只要定义了,就是常数或者nac?这里难道说y或者z有可能是undef么?那么程序本身就有可能不通过语法检查?
这个时候,先meet后meet的区别就体现出来了。
Worklist Algow Vi
就是加了当前需要更改的节点集合Worklist。


