UVa LA 4253 & UVa 1421 Archery 枚举，状态削减，oj错误题目 难度: 1

题目

https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=4167

 

题意

有n+1条平行于x轴的线段，最底下的线段是[0, w]，站在最下面的第0条线段上的某个点上，问有没有一条过该点的直线也通过上面的n条线段。2<=n<=5000，2<=w<=1e7，保证这n+1条线段高度都不同。最高的线段到第0条线段高度差（y坐标差）不超过n，数据保证每条线段高度不同。对于第i条线段，其左右端点横坐标Li，Ri必然满足0<=Li<Ri<=W。第i条线段高度Di满足0<=Di<=W。Li,Ri,Di都是整数，这样精度问题较小。

 

思路

想到直线就会想到两点式或者点斜式。这里两点式一定会TLE。因此只能是点斜式了，枚举斜率并不是一个很好的做法。因此，可以枚举直线上一点，然后通过斜率来看有没有符合结果的直线。由于直线可以平移，因此总可以平移到一种同时经过第i条线段左端点和第k条线段右端点的情况。因此只需要枚举这n+1条线段的左端点。

对于第i条线段的左端点(Li,Di)，如果有一条经过(Li,Di)的直线经过全部n+1条线段，则可以输出"YES"，否则，还要继续枚举下一线段的左端点。或者可以说，如对(Li,Di)，存在斜率k（k可能为无穷）使得对应直线经过全部n+1条线段，则满足题意

由于线段是平行于x轴的，所以不会产生跨x轴的情况，那么就可以维护每条肽段所对应的可行斜率的集合，如果这些集合的并集非空，那么就有符合结果的直线存在。

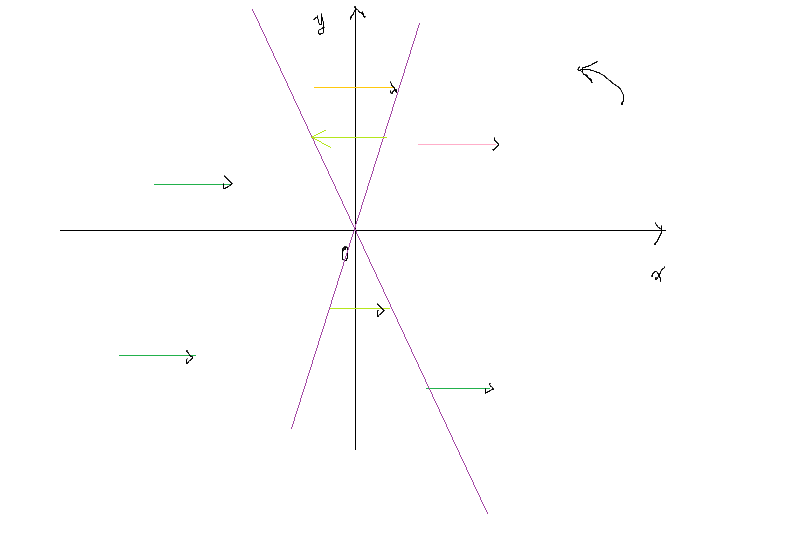
但是直接维护斜率存在要过90度的情况，因此，可以以(Li,Di)为中心建立极坐标系，维护线段所对应角度。如果比Di高，对应区间为(Ri, Di)对应极角到(Li, Di)对应极角这个封闭区间。如果比Di低，也就是在x轴下方，总可以不失意义转换为x轴上方的对应方向相反的区间。

 

感想：

1. 注意如果把scanf("%d%d", R, &n) == 2作为判断条件，就会wa，这一般是因为测试数据中有冗余

2. 一开始枚举了两条线段的端点<左，左>，<左，右>，<右，左>，<右，右>四种情况，所以一直TLE。但是因为必然可以平移到既有左端点又有右端点，所以直接枚举遍历左或者右端点就够了

3. 精度倒不用特别注意

代码

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <cstring>
#include <vector>
#include <map>
#include <set>
using namespace std;
typedef pair<int, int> Pair;
typedef long long ll;
const int MAXN = 5e3 + 4;
const double pie = acos(-1.0);
int n;
int D[MAXN];
int L[MAXN];
int R[MAXN];
bool simplecheck() {
    int mnX = 0;
    int mxX = R[0];
    for (int i = 0; i <= n; i++) {
        mnX = max(mnX, L[i]);
        mxX = min(mxX, R[i]);
    }
    return mnX <= mxX;

}

double getK(int x0, int x1, int y0, int y1) {
    return (y1 - y0) * 1.0 / (x1 - x0);
}

double getAng(int x0, int x1, int y0, int y1) {
    if (x0 == x1)return pie / 2;
    double ang = atan(getK(x0, x1, y0, y1));
    if (ang < 0)return ang + pie;
    return ang;
}

void getAngInterval(int x0, int y0, int i, double& a0, double& a1) {
    if (D[i] == y0) {
        a0 = 0;
        a1 = pie;
    }
    else if (D[i] > y0) {
        a0 = getAng(x0, R[i], y0, D[i]);
        a1 = getAng(x0, L[i], y0, D[i]);
    }
    else {
        a0 = getAng(x0, L[i], y0, D[i]);
        a1 = getAng(x0, R[i], y0, D[i]);
    }
}
int main() {
    int T;
    freopen("C:\\Users\\Iris\\source\\repos\\ACM\\ACM\\input.txt", "r", stdin);
    freopen("C:\\Users\\Iris\\source\\repos\\ACM\\ACM\\output.txt", "w", stdout);
    scanf("%d", &T);
    //cin >> T;
    for (int ti = 1; ti <= T; ti++) {
        scanf("%d%d", R, &n);
        for (int i = 1; i <= n; i++) {
            scanf("%d%d%d", D + i, L + i, R + i);
        }
        bool fl = simplecheck();
        if (!fl) {
            for (int i = 0; i <= n; i++) {
                double amn = 0, amx = pie;
                bool ok = true;
                for (int j = 0; j <= n && ok; j++) {
                    double amnnow, amxnow;
                    getAngInterval(L[i], D[i], j, amnnow, amxnow);
                    if (amnnow > amx) {
                        ok = false;
                        break;
                    }
                    if (amxnow < amn) {
                        ok = false;
                        break;
                    }
                    amn = max(amn, amnnow);
                    amx = min(amx, amxnow); 
                    //printf("From (%d, %d) to (%d, %d)->(%d, %d), ang [%.2f, %.2f], Overall [%.2f, %.2f]\n", L[i], D[i], L[j], D[j], R[j], D[j], amnnow * 180.0 / pie, amxnow * 180.0 / pie, amn * 180.0 / pie, amx * 180.0 / pie);

                }
                if (ok) {
                    fl = true;
                    break;
                }
            }
        }
        if (fl) {
            puts("YES");
        }
        else puts("NO");
    }
    return 0;
}