学数答题160912-导数极值点偏移

题160912（14分）若函数$f\left( x \right)={{e}^{x}}-a\ln x-a$（$a>e$）有两个零点${{x}_{1}},{{x}_{2}}$，求证：${{x}_{1}}+{{x}_{2}}>2$．

---

证明：函数$y=f\left( x \right)$的零点，即方程$\dfrac{1}{a}={{\text{e}}^{-x}}\left( \ln x+1 \right)$的根，

设$g\left( x \right)={{\text{e}}^{-x}}\left( \ln x+1 \right)$，因此${{x}_{1}},{{x}_{2}}$是方程$g\left( x \right)=\dfrac{1}{a}$的两个实根．

$g\left( x \right)$的导数$g'\left( x \right)={{e}^{-x}}\left( \dfrac{1}{x}-\ln x-1 \right)$，

当$x\in \left( 0,1 \right)$时，$g'\left( x \right)>0$，$g\left( x \right)$单增；当$x\in \left( 1,+\infty  \right)$上时，$g'\left( x \right)<0$，$g\left( x \right)$单减，

$x=1$是$g\left( x \right)$的极大值点．

故方程$g\left( x \right)=\dfrac{1}{a}$的两个实根一个比$1$大，一个比$1$小，不妨设${{x}_{1}}<1<{{x}_{2}}$．

构造函数$h\left( x \right)=-\dfrac{1}{\text{e}}{{\left( x-1 \right)}^{2}}+\dfrac{1}{\text{e}}$，令$F\left( x \right)=g\left( x \right)-h\left( x \right)$，

则${F}'\left( x \right)={g}'\left( x \right)-{h}'\left( x \right)={{\text{e}}^{-x}}\left( \dfrac{1}{x}-\ln x-1 \right)+\dfrac{2}{\text{e}}\left( x-1 \right)$，

于是${{F}'}'\left( x \right)={{\text{e}}^{-x}}\left( -\dfrac{1}{{{x}^{2}}}-\dfrac{2}{x}+\ln x+1 \right)+\dfrac{2}{\text{e}}$，

因为$y=-\dfrac{1}{{{x}^{2}}}-\dfrac{2}{x}+\ln x+1$在$\left( 0,+\infty  \right)$上单调递增，

所以当$x\in \left( 0,1 \right)$时，${{F}'}'\left( x \right)<-2{{\text{e}}^{-x}}+\dfrac{2}{\text{e}}<-2{{\text{e}}^{-1}}+\dfrac{2}{\text{e}}=0.$

当$x\in \left( 1,+\infty  \right)$时，$F''\left( x \right)>-2{{\text{e}}^{-x}}+\dfrac{2}{\text{e}}>-2{{\text{e}}^{-1}}+\dfrac{2}{\text{e}}=0,$

所以${F}'\left( x \right)$在$\left(0,1\right)$上单调递减，在$\left(1,+\infty\right)$上单调递增，且${F}'\left( 1 \right)=0$，

所以${F}'\left( x \right)0$，$x\in \left( 0,+\infty  \right)$．

所以$F\left(x\right)$单调递增，又$F\left(1\right)=0$，所以有$g\left(x\right)-h\left(x\right)\begin{cases}>0,x>1,\\=0,x=1,\\<0,0<x<1.\end{cases}$

设$y=\dfrac{1}{a}$与二次函数$h\left(x\right)$交于$x_3,x_4$两点，不妨设$x_3<1<x_4$．因此，有

$\dfrac{1}{a}=h\left( {{x}_{3}} \right)=g\left( {{x}_{1}} \right)<h\left( {{x}_{1}} \right)$，$\dfrac{1}{a}=h\left( {{x}_{4}} \right)=g\left( {{x}_{2}} \right)>h\left( {{x}_{2}} \right)$，

如图所示：

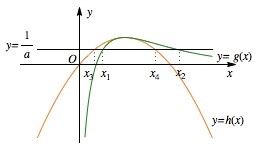
所以$x_3<x_1<1<x_4<x_2,$

因为$x_3+x_4=2$，所以${{x}_{1}}+{{x}_{2}}>2$，得证．

注：本解析是通过构造二次函数$h\left(x\right)$，比较$g\left(x\right)$与$h\left(x\right)$在极值点两侧的大小关系，结合函数的单调性，得到$x_1,x_2,x_3,x_4$的大小关系，从而由$h\left(x\right)$与$y=\dfrac{1}{a}$交点的横坐标之和为$2$，得到$x_1+x_2$与$2$的大小关系．难点是如何构造这样的二次函数，$g\left(x\right)$的极值点为$1$，则此二次函数$h\left(x\right)$需要满足$h\left( 1 \right)=g\left( 1 \right)$，${h}'\left( 1 \right)={g}'\left( 1 \right)$，${{h}'}'\left( 1 \right)={{g}'}'\left( 1 \right)$，

所以$h\left( x \right)=\dfrac{{g}'\left( 1 \right)}{2}{{\left( x-1 \right)}^{2}}+g\left( 1 \right).$