无痛机器学习之VAE

全文内容来自对https://zhuanlan.zhihu.com/p/22464760、https://zhuanlan.zhihu.com/p/22464764、https://zhuanlan.zhihu.com/p/22464768和https://zhuanlan.zhihu.com/p/22684931的整合。

一、KL散度

前面我们介绍了GAN——Generative Adversarial Network，这个网络组是站在对抗博弈的角度去展现生成模型和判别模型各自的威力的，下面我们来看看这种生成模型和判别模型组合的另一个套路——Variational autoencoder，简称VAE。Variational autoencoder的概念相对复杂一些，它涉及到一些比较复杂的公式推导。在开始正式的推导之前，我们先来看看一个基础概念——KL divergence，翻译过来叫做KL散度。

什么是KL散度

无论从概率论的角度，还是从信息论的角度，我们都可以很好地给出KL散度测量的意义。在Variational Inference中，我们希望能够找到一个相对简单好算的概率分布q，使它尽可能地近似我们待分析的后验概率p(z|x)，其中z是隐变量，x是显变量。在这里我们的“loss函数”就是KL散度，他可以很好地测量两个概率分布之间的距离。如果两个分布越接近，那么KL散度越小，如果越远，KL散度就会越大。

KL散度的公式为：

$KL(p||q)=\sum{p(x)log\frac{p(x)}{q(x)}}$ ，这个是离散概率分布的公式，

$KL(p||q)=\int{p(x)log{\frac{p(x)}{q(x)}}dx}$ ，这个是连续概率分布的公式。

KL散度的实战——1维高斯分布

我们先来一个相对简单的例子。假设我们有两个随机变量x1,x2，各自服从一个高斯分布 $N_1(\mu_1,\sigma_1^2),N_2(\mu_2,\sigma_2^2)$ ，那么这两个分布的KL散度该怎么计算呢？

我们知道

$N(\mu,\sigma)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{\frac{(x-\mu)^2}{2\sigma^2}}$

那么KL(p1,p2)就等于

$\int{p_1(x)log\frac{p_1(x)}{p_2(x)}}dx$
$=\int{p_1(x)(log{p_1(x)}}dx-log{p_2(x)})dx$

$=\int{p_1(x)}*(log{\frac{1}{\sqrt{2\pi\sigma_1^2}}e^{\frac{(x-\mu_1)^2}{2\sigma_1^2}}}-log{\frac{1}{\sqrt{2\pi\sigma_2^2}}e^{\frac{(x-\mu_2)^2}{2\sigma_2^2}}})dx$
$=\int{p_1(x) *(-\frac{1}{2}log2\pi-log{\sigma_1}-\frac{(x-\mu_1)^2}{2\sigma_1^2}}+ \frac{1}{2}log{2\pi}+log{\sigma_2}+\frac{(x-\mu_2)^2}{2\sigma_2^2})dx$
$=\int{p_1(x)(log\frac{\sigma_2}{\sigma_1}+[\frac{(x-\mu_2)^2}{2\sigma_2^2}-\frac{(x-\mu_1)^2}{2\sigma_1^2}])dx}$
$=\int(log\frac{\sigma_2}{\sigma_1})p_1(x)dx+\int(\frac{(x-\mu_2)^2}{2\sigma_2^2})p_1(x)dx-\int(\frac{(x-\mu_1)^2}{2\sigma_1^2})p_1(x)dx$
$=log\frac{\sigma_2}{\sigma_1}+\frac{1}{2\sigma_2^2}\int((x-\mu_2)^2)p_1(x)dx-\frac{1}{2\sigma_1^2}\int((x-\mu_1)^2)p_1(x)dx$

（更新）到这里停一下，有童鞋问这里右边最后一项的化简，这时候积分符号里面的东西是不看着很熟悉？没错，就是我们常见的方差嘛，于是括号内外一约分，就得到了最终的结果—— $\frac{1}{2}$ 。

好，继续。
$=log\frac{\sigma_2}{\sigma_1}+\frac{1}{2\sigma_2^2}\int((x-\mu_2)^2)p_1(x)dx-\frac{1}{2}$
$=log\frac{\sigma_2}{\sigma_1}+\frac{1}{2\sigma_2^2}\int((x-\mu_1+\mu_1-\mu_2)^2)p_1(x)dx-\frac{1}{2}$
$=log\frac{\sigma_2}{\sigma_1}+\frac{1}{2\sigma_2^2}[\int{(x-\mu_1)^2}p_1(x)dx+\int{(\mu_1-\mu_2)^2}p_1(x)dx+2\int{(x-\mu_1)(\mu_1-\mu_2)]}p_1(x)dx-\frac{1}{2}$
$=log\frac{\sigma_2}{\sigma_1}+\frac{1}{2\sigma_2^2}[\int{(x-\mu_1)^2}p_1(x)dx+(\mu_1-\mu_2)^2]-\frac{1}{2}$

$=log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2}$

假设N2是一个正态分布，也就是说 $\mu_2=0,\sigma_2^2=1$ ，也就是说

$KL(\mu_1,\sigma_1)=-log\sigma_1+\frac{\sigma_1^2+\mu_1^2}{2}-\frac{1}{2}$ 。

那么N1长成什么样子能够让KL散度尽可能地小呢？

我们用“肉眼”看一下就能猜测到当 $\mu_1=0,\sigma_1=1$ 时，KL散度最小。从公式中可以看出，如果 $\mu_1$ 偏离了0，那么KL散度一定会变大。而方差的变化则有些不同：

当 $\sigma_1$ 大于1时， $\frac{1}{2}\sigma_1^2$ 将越变越大，而 $-log\sigma_1$ 越变越小；

当 $\sigma_1$ 小于1时， $\frac{1}{2}\sigma_1^2$ 将越变越小，而 $-log\sigma_1$ 越变越大；

那么哪边的力量更强大呢？我们可以作图出来：

import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0.5,2,100)
y = -np.log(x)+x*x/2-0.5
plt.plot(x,y)
plt.show()

从图中可以看出

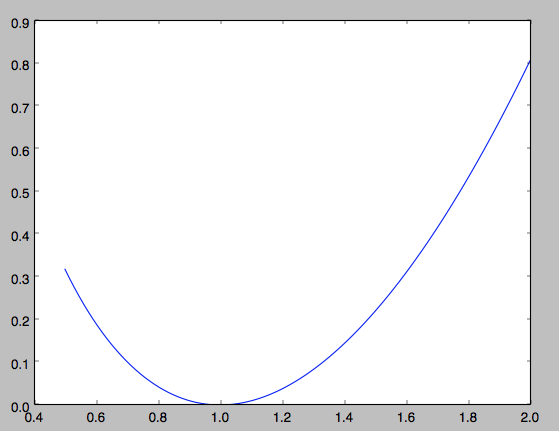
二次项的威力更大，函数一直保持为非负，这和我们前面提到的关于非负的定义是完全一致的。

好了，看完了这个简单的例子，下面让我们再看一个复杂的例子。

一个更为复杂的例子：多维高斯分布的KL散度

上一回我们看过了1维高斯分布间的KL散度计算，下面我们来看看多维高斯分布的KL散度是什么样子？说实话，这一次的公式将在后面介绍VAE时发挥很重要的作用！

首先给出多维高斯分布的公式：

$p(x_1,x_2,...x_n)=\frac{1}{\sqrt{2\pi*det(\Sigma)}}e^{(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))}$

由于这次是多维变量，里面的大多数计算都变成了向量、矩阵之间的计算。我们常用的是各维间相互独立的分布，因此协方差矩阵实际上是个对角阵。

考虑到篇幅以及实际情况，下面直接给出结果:

$KL(p1||p2)=\frac{1}{2}[log \frac{det(\Sigma_2)}{det(\Sigma_1)} - d + tr(\Sigma_2^{-1}\Sigma_1)+(\mu_2-\mu_1)^T \Sigma_2^{-1}(\mu_2-\mu_1)]$

我们展示VAE效果的时候，就会让大家看到KL散度的作用。

坚持看到这里的童鞋是有福的，来展示一下VAE的解码器在MNIST数据库上产生的字符生成效果：

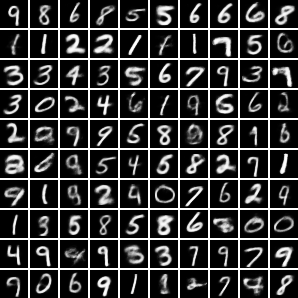
从这个效果上来看，它的功能和GAN是有点像的，那么让我们来进一步揭开它的庐山真面目吧！

二、基本思想

上一回我们花了很大的篇幅介绍了KL散度，这一回我们来看看VAE，尤其是深度模型下的VAE。

前面我们已经见过了许多优秀的深度学习模型，它们达到了非常好的精度和效果。众人曾十分认真地分析过为什么这些模型的效果这么好，结论是深度模型的非线性拟合能力确实很强。不管曾经多么复杂的问题，一个深度模型出马，立刻把问题解决的八九不离十。VAE也是利用了这个特点，我们用深度模型去拟合一些复杂的函数，从而解决实际问题。

让我们先记住这个trick，后面我们会用到它。接下来我们要上场的是生成模型。前面我们看过的很多模型从原理上来说都是判别式模型。我们有一个等待判别的事物X，这个事物有一个类别y，我们来建立一个模型f(x;w)，使得p(y|X)的概率尽可能地大，换种方法说就是让f(x;w)尽可能地接近y。

如果我们想用生成式的模型去解决这个问题，就需要利用贝叶斯公式把这个问题转换过来：

$p(z|X)=\frac{p(X|z)p(z)}{p(X)}$

为了遵从大多数教科书上的变量用法，这里将y变成了z。当然，这个时候的z可能比上面提到的“类别”y要复杂一些。在很多的生成模型中，我们把z称作隐含变量，把X称作观测变量。一般来说，我们可以比较容易地观察到X，但是X背后的z却不那么容易见到，而很多时候X是由z构造出来的，比方说一天的天气好与坏是由很多不易观察的因素决定的。于是我们自然而然就有了一个需求，当我们拿到这些X之后，我们想知道背后的z是什么，于是乎就有了上面那个公式。

对于一些简单的问题，上面的公式还是比较容易解出的，比方说朴素贝叶斯模型，但是还是有很多模型是不易解出的，尤其当隐含变量处于一个高维度的连续空间中：

$p(z|X)=\frac{p(X|z)p(z)}{\int_z{p(X|z)p(z)dz}}$

这里的积分就没那么容易搞定了。于是乎，各路大神开始想尽一切办法让上面的式子变得好解些。

这时候我们难免会冒出一个问题，既然有了判别式模型可以直接求解式子左边的那个东西，为什么非要把它变成右边那一大堆东西，搞得自己不方便解呢？其实谁都不想给自己找麻烦，可问题是右边的这一堆除了能够解这个问题，它还有一个更加高级的功能，就是根据模型随机生成X。

我们可以想想看，如果我们只拥有式子左边的p(z|X)，我们想要生成一个符合某种z的X该怎么办？

第一步，随机一个X；
第二步，用p(z|X)计算概率，如果概率满足，则结束，如果不满足，返回第一步；

于是乎，用判别式模型生成X变成了人品游戏，谁也不知道自己什么时候能在第二步通过。而生成式模型就不同了，我们可以按需定制，首先确定好z，然后根据p(X|z)进行随机采样就行了，生成X的过程安全可控。

说了这么多，下面我们正式进入公式推导的部分。

Variational Inference

虽然我们鼓吹了很多生成模型的好处，但是面对等号右边那一堆东西，该束手无策还是束手无策。但是，前辈们还是想到了一些精妙的解法。既然用概率论的方法很难求出右边的东西，我们能不能做一些变换，比方说——（略显生硬地）我们用一个variational的函数q(z)去代替p(z|X)？别着急，后面我们会看到它带来的好处的。

这里的variational inference介绍的有点简单，有机会我们再详细介绍下。

既然要用q(z)这个新东西去代替p(z|X)，那么我们当然希望两个东西尽可能地相近，于是乎我们选择了KL散度这个指标用来衡量两者的相近程度。由于两边都是可以看作针对z的概率分布，因此用KL散度这个指标实际上非常合适。

所以就有了：

$KL(q(z)||p(z|X))=\int{q(z)log \frac{q(z)}{p(z|X)}}dz$
$=\int{q(z)[log q(z) - log p(z|X)]}dz$

我们做一下贝叶斯公式的变换，就得到了：

$=\int{q(z)[log q(z) - log p(X|z) - log p(z) + logp(X)]}dz$

再将和z无关的项目从积分符号中拿出来，就得到了：

$=\int{q(z)[log q(z) - log p(X|z) - log p(z)]}dz + log p(X)$

左右整理一下，就得到了：

$log p(X) - KL(q(z)||p(z|X))=\int{q(z) log p(X|z)}dz-KL(q(z)||p(z))$

好吧，其实整理了一圈，这个公式还是很乱，不过因为KL散度的特殊关系，我们还是从这个公式中看到了一丝曙光：

我们虽然不大容易求出p(X)，但我们知道当X给定的情况下，p(X)是个固定值。那么如果我们希望KL(q(z)||p(z|X))尽可能地小，也就相当于让等号右边的那部分尽可能地大。其中等号右边的第一项实际上是基于q(z)的似然期望，第二项又是一个负的KL散度，所以我们可以认为，为了找到一个好的q(z)，使得它和p(z|X)尽可能地相近，我们需要：

右边第一项的log似然的期望最大化
右边第二项的KL散度最小化

对于VAE之前的variation inference（中文可以翻译成变分推断），到这里我们就要开始一段全新的公式推导了。比方说我们做一个mean-field assumption（说实话我不太知道mean-field怎么翻译更直观，于是就把英文放在这里了），于是乎对于多个隐含变量组成的z，分量相互之间是独立的，于是根据这个特性，我们又可以进行进一步地公式化简。由于我们今天的主题是VAE，所以关于这部分我们就不再赘述了。这时候我们又想起了文章开头我们提到的一句话：

“VAE也是利用了这个特点，我们用深度模型去拟合一些复杂的函数”

那么是时候让这句话发挥作用了，不过关于它发挥的方法我们下回再说。

三、公式与实现

Variational Autoencoder

终于要见到正主了。让我们关注一下variational inference公式的右边，在此之前我们要对公式进行一定的变化，然后给出我们的详细建模过程。

Reparameterization Trick

为了更加方便地求解上面的公式，这里我们需要做一点小小的trick工作。上面提到了Q'(z|X)这个变分函数，它代表了当我们给定某个X的情况下z的分布情况。我们可以想象这里的z是满足某种分布的。那么我们从数值上可以把X抽离出来呢？

比方说我们有一个随机变量a服从高斯分布N(1,1)，根据定理我们可以定义一个随机变量b=a-1，那么它将服从高斯分布N(0,1)，换句话说，我们可以用一个均值为0，方差为1的随机变量加上1来表示现在的随机变量a。这样我们就把一个随机变量分成了两部分——一部分是确定的，一部分是随机的。

对于上面的Q'(z|X)，我们同样可以采用上面的方法完成。我们可以把一个服从这个条件概率的z拆分成两部分，一部分是一个复杂的函数 $g_\phi(X)$ ，它解决了确定部分的问题，我们再定义另外一个随机变量 $\varepsilon$ ，它负责随机的部分。为了书写的一致性，我们用 $g_\phi(X+\varepsilon )$ 来表示服从条件概率的z。

这样做有什么好处呢？现在我们知道了z条件概率值完全取决于生成它所使用的 $\varepsilon$ 的概率。也就是说如果 $z^{(i)}=g_\phi(X+\varepsilon^{(i)} )$ ，那么 $q(z^{(i)})=p(\varepsilon ^{(i)})$ ，那么上面关于变分推导的公式也就变成了下面的公式：

$log p(X) - KL(q(z)||p(z|X))=\int{p(\varepsilon ) log p(X|g_{\phi}(X,\varepsilon ) )}dz-KL(q(z|X,\varepsilon )||p(z))$

这就是替换的一小步，求解的一大步！实际上到了这里，我们已经接近问题最终的答案了，剩下的只是我们的临门一脚——我们可不可以假设这个随机部分服从什么样的分布呢？

当然能！不过由于我们一般把z的先验假设成一个多维的独立高斯分布，为了KL计算的方便，也为了我们在前面的章节推导2个多维高斯分布的KL散度这件事情没有白做，我们决定在这里让这个替换后的随机部分同样服从多维的独立高斯分布。

下面我们来看看这个公式的两部分具体该如何计算。

右边的第二项，KL散度部分——encoder

首先来看看公式右边的第二项。刚才我们提到我们一般把z的先验假设成一个多维的独立高斯分布，这里我们可以给出一个更强的假设，那就是这个高斯分布的均值为0，方差为单位矩阵，那么我们前面提到的KL散度公式瞬间简化成为：

$KL(p1||N(0,I))=\frac{1}{2}[-log [det(\Sigma_1)] - d + tr(\Sigma_1)+\mu_1^T \mu_1]$

真的有种世界清静了的感觉……我们下面的目标就是利用encoder的部分根据X求解z的均值方差。这部分我们采用一个深度的神经网络就可以了。由于实际训练过程中我们采用的是batch的训练方法，因此我们需要输入一个batch的X信息，然后进行模型的计算和优化。

如果我们用一个向量 $\sigma_1$ 来表示上面协方差矩阵的主对角线，情况将会更加美好：

$KL(p1(\mu_1,\sigma_1)||N(0,I))=\frac{1}{2}[-\sum_i{log [(\sigma_{1i})}] - d + \sum_i(\sigma_{1i})+\mu_1^T \mu_1]$

到这里，关于这一部分的函数拟合已经比较清晰了，我们的函数输入输出已经非常清楚，我们的loss也化简到了一个比较简单的状态，下面就是具体的计算了。

右边的第一项，期望部分——decoder

从前面的KL散度公式优化中，我们可以看到，如果两个概率分布的KL散度值为0时，实际上就说明我们的随机部分的分布和我们z的先验分布相同了。

这带来一个好消息，就是我们可以直接使用上一步encoder得到的均值方差。这样，我们就需要另外一个深度函数decoder，帮助我们从z再变回X。前面我们说了我们的目标是最大化似然的期望，实际上就可以转换为采样一批X，先用encoder生成z‘的分布，然后通过优化使得p(X|z)的似然最大化。

关于如何最大化似然，我们有很多办法，这一部分将在实践的环节详细给出。

好了，到这里，实际上VAE的核心计算推导就结束了。

四、实现

终于到了实现的地方。前面干燥乏味的公式推导和理论阐述已经让很多人昏昏欲睡了，下面我们要提起精神，来看看这个模型的一个比较不错的实现——GitHub - cdoersch/vae_tutorial: Caffe code to accompany my Tutorial on Variational Autoencoders，当然，这个实现也是一个配套tutorial文章的实现。感兴趣的童鞋也可以看看这篇tutorial，相信会对这个模型有更多的启发。

这个实现的目标数据集是MNIST，这和我们之前的DCGAN是一样的。当然，在他的tutorial中，他一共展现了3个模型。下面我们就从prototxt文件出发，先来看看我们最熟悉的经典VAE。

VAE

说实话一看他在github给出的那张图，即使是有一定的VAE模型基础的童鞋也一定会感觉有些发懵。我们将模型中的一些细节隐去，只留下核心的数据流动和loss计算部分，那么这个模型就变成了下面的样子：

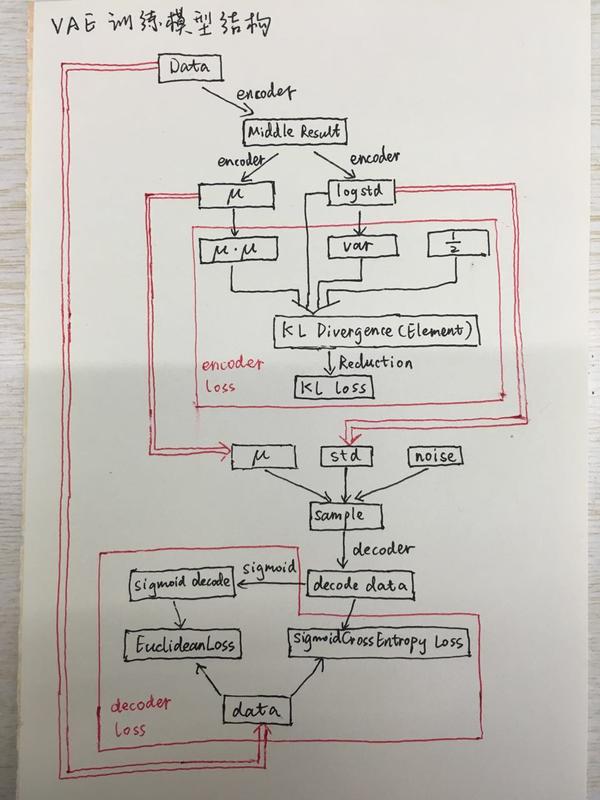
图中的黑色的框表示数据的流动，红色的框表示求loss的地方。双红线表示两个不同部分的数据共享。可以看出图的上边是encoder的部分，也就是从X到z的过程，下面是从z到X的过程。前面的文章中我们给出了求解的公式，现在我们给出了这个网络模型，我们可以把这两部分对照起来。

另外其中的encoder和decoder部分被省略了，在实际网络中，我们可以用一个深度神经网络模型代替。除此之外，图中还有三个主要部分：

首先是q(z|X)的loss计算。
其次是z的随机生成。
最后是p(X|z)的loss计算。

这其中最复杂的就是第一项，q(z|X)的loss计算。由于caffe在实际计算过程中主要采用向量的计算方式，所以前面的公式需要进行一定的变换：

$KL(p1(\mu_1,\sigma_1)||N(0,I))=\frac{1}{2}[-\sum_i{log [(\sigma_{1i})}] - d + \sum_i(\sigma_{1i})+\mu_1^T \mu_1]$
$=\sum_{i=0}^{d}{-\frac{1}{2}log[std_{1i}^2]}+\sum_{i=0}^{d}(-\frac{1}{2})+\sum_{i=0}^d\frac{1}{2}(std_{1i}^2)+\sum_{i=0}^d\frac{1}{2}[\mu_{1i}^2]$
$=\sum_{i=0}^{d}[{-\frac{1}{2}log[std_{1i}^2]}+\frac{1}{2}(std_{1i}^2)+\frac{1}{2}[\mu_{1i}^2]+(-\frac{1}{2})]$

在完成了前面的向量计算后，最后一步是做Reduction，也就是完成加和的过程。这样就使得计算可以顺利完成。

看懂了这些部分，再加上前面我们对VAE的了解，相信我们对VAE模型有了更加清晰的认识。

MNIST生成模型可视化

下面这张图是一次实验过程中产生的，看上去有点像所有数字在一个平面的分布，数字与数字之间还存在着一定的过渡区域。那么这张图是如何产生的呢？

一个比较简单的方法，就是把z的维度设为2。以下就是这幅图生成的过程：

利用VAE模型进行训练，得到了模型中的 $\mu$ 和 $\sigma$
完成z的采样过程，我们在二维空间内按照N(0,I)有规律地进行采样noise，把noise、 $\mu$ 和 $\sigma$ 结合起来
把得到采样后的z，最后利用decoder把z转换成X，显示出来

经过这样几步我们就可以得到最终的图像了。实际上我们前面提过的GAN模型也可以用类似的方法生成这样的图像。

posted @ 2017-09-27 16:01 雪球球阅读(2380) 评论(0) 编辑收藏举报

刷新页面返回顶部