x86---32汇编(1)---乘除法

　　最近想优化一下代码的运行速度，笔者就想着汇编的效率比较高，所以就看网上的一些书籍，

练习了一下汇编，乘除法的指令imul和idiv。

代码：

#include <stdio.h>
#include <tchar.h>


extern "C" int IntegerMulDive_(int a, int b, int *prod, int *quo, int *rem);

int _tmain(int argc, _TCHAR* argv[])
{
    int a = 21, b = 9;
    int prod = 0, quo = 0, rem = 0;
    int rc;
    rc = IntegerMulDive_(a, b, &prod, &quo, &rem);
    printf("Input1-a:%4d b:%4d\n", a, b);
    printf("Output1-rc:%4d prod:%4d\n",rc,prod);
    printf("quo:%4d rem:%4d\n\n", quo, rem);

    a = -29;
    prod = quo = rem = 0;
    rc = IntegerMulDive_(a, b, &prod, &quo, &rem);
    printf("Input2-a:%4d b:%4d\n", a, b);
    printf("Output-2-rc:%4d prod:%4d\n",rc,prod);
    printf("quo:%4d rem:%4d\n\n", quo, rem);

    b = 0;
    prod = quo = rem = 0;
    rc = IntegerMulDive_(a, b, &prod,&quo, &rem);
    printf("Input3-a:%4d b:%4d\n", a, b);
    printf("Output3-rc:%4d prod:%4d\n", rc, prod);
    printf("quo:%4d rem:%4d\n\n", quo, rem);


    return 0;
}

    .model flat,c
    .code

; extern "C" int IntegerMulDiv_(int a, int b, int* prod, int* quo, int*rem);
; Description: This function demonstrates use of the imul and idiv
; instructions. It also illustrates pointer usage.
;
; Returns: 0 Error (divisor is zero)
; 1 Success (divisor is zero)
;
; Computes: *prod = a * b;
; *quo = a / b
; *rem = a % b

IntegerMulDive_ proc
;Function prolog
    push ebp
    mov ebp,esp
    push ebx

;Make sure the divisor is not zero
    xor eax,eax            ;set error return code
    mov ecx,[ebp+8]        ;ecx='a'
    mov edx,[ebp+12]    ;edx='b'
    or edx,edx
    jz InvalidDivisor    ;jump if 'b' is zero

;Calulate product and save result
    imul edx,ecx        ;edx='a'*'b'
    mov ebx,[ebp+16]    ;ebx='prod'
    mov [ebx],edx        ;save product

;Calculate quotient and remainder,save results
    mov eax,ecx            ;eax='a'
    cdq                    ;edx:eax contains dividend
    idiv dword ptr [ebp+12]        ;eax=quo,edx=rem

    mov ebx,[ebp+20]            ;ebx='quo'
    mov [ebx],eax                ;save quotient
    mov ebx,[ebp+24]            ;ebx='rem'
    mov [ebx],edx                ;save remainder
    mov eax,1                    ;set success return code

;Function epilog
InvalidDivisor:
    pop ebx
    pop ebp
    ret
IntegerMulDive_ endp
    end

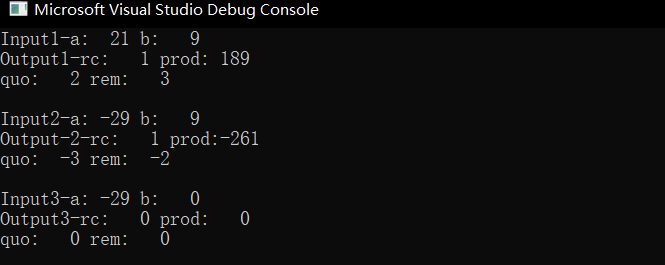
运行效果：