图(一)
图(Graph)
图(graph)是一种比线性表、树更为复杂的数据结构。在线性表中,数据元素之间呈线性关系,即每个元素只有一个直接前驱和一个直接后继。在树型结构中,数据元素之间有明显的的层次关系,即每个结点只有一个直接前驱,但可有多个直接后继,而在图结构中,每个结点即可有多个直接前驱,也可有多个直接后继,因此,树结构是图结构的一种特殊情形。当一个树结构中允许同一结点出现在不同分支上时,该树结构实际上就是一个图结构。
邻接:如果两个顶点被同一条边连接,就称这两个顶点是邻接的。
路径:边的序列。
连通图:至少有一条路径可以连接器所有的顶点,这个图就称为连通图。
有向图:如果边是没有方向的,称为无向图,反之为有向图。
带权图:在某些图,边被赋予一种权值,权值是一个数字,它代表两个顶点的物理距离,或时间或花费,这种图称为带权图。
图的存储结构
1)邻接矩阵
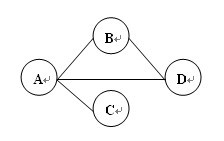
邻接矩阵是一个二维数组,数据项表示两点间是否存在边,如果图有 N 个顶点,则邻接矩阵就是 N*N 的数组。两个顶点间有边的表示为1,没有边则为0。也可以用 boolean 表示。
| A | B | C | D | |
| A | 0 | 1 | 1 | 1 |
| B | 1 | 0 | 0 | 1 |
| C | 1 | 0 | 0 | 0 |
| D | 1 | 1 | 0 | 0 |
| 顶点 | 包含邻接顶点的链表 |
| A | B -> C -> D |
| B | A -> D |
| C | A |
| D | A -> B |
在邻接表中,符号 -> 表示链表中的一个节点,每个节点都是一个顶点。邻接表仅表示了当前顶点与哪些顶点连接,与顶点顺序无关。
顶点代码:
public class Vertex { private char label; private boolean isVisited; public Vertex(char label) { this.label = label; } public char getLabel() { return label; } public boolean isVisited() { return isVisited; } public void setVisited(boolean isVisited) { this.isVisited = isVisited; } }
图的代码:
public class Graph0 { private final int MAX_VERTS = 20; private Vertex[] vertexArray; private int[][] adjMat; private int nVerts; public Graph0() { vertexArray = new Vertex[MAX_VERTS]; adjMat = new int[MAX_VERTS][MAX_VERTS]; nVerts = 0; } public void addVertex(char label) { vertexArray[nVerts++] = new Vertex(label); } public void addEdge(int start, int end) { adjMat[start][end] = 1; adjMat[end][start] = 1; } }
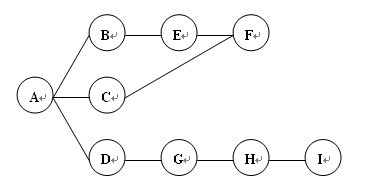 图x
图x
图的遍历
1)深度优先遍历
深度优先要得到距离起始点最远的顶点,然后再不能继续前进的时候返回。栈的内容是从起始点到各个顶点访问的整个过程。
规则:
- 如果可能,访问一个邻接的未访问顶点,标记它,放入栈中。
- 当不能执行规则1,如果栈不空,则从栈中弹出一个顶点。
- 如果不能执行规则1、规则2,就完成了整个遍历过程。
public class StackX { private final int SIZE; private int[] array; private int top; public StackX(int size) { this.SIZE = size; array = new int[SIZE]; top = -1; } public void push(int i) { array[++top] = i; } public int pop() { return array[top--]; } public int peek() { return array[top]; } public boolean isEmpty() { return top == -1; } }
public class Graph { private final int MAX_VERTS; private Vertex[] vertexArray; private int[][] adjMat; private StackX stack; private int nVerts; public Graph(int verts) { this.MAX_VERTS = verts; vertexArray = new Vertex[MAX_VERTS]; adjMat = new int[MAX_VERTS][MAX_VERTS]; stack = new StackX(MAX_VERTS); nVerts = 0; } public void addVertex(char label) { vertexArray[nVerts++] = new Vertex(label); } public void addEdge(int start, int end) { adjMat[start][end] = 1; adjMat[end][start] = 1; } public void displayVertex(int index) { System.out.print(vertexArray[index].getLabel() + " -> "); } //depth first search public void dfs() { vertexArray[0].setVisited(true); displayVertex(0); stack.push(0); while (!stack.isEmpty()) { int v = getAdjUnvisitedVertex(stack.peek()); if (v == -1) { stack.pop(); } else { vertexArray[v].setVisited(true); displayVertex(v); stack.push(v); } } for (int j = 0; j < MAX_VERTS; j++) { if (vertexArray[j] != null) { vertexArray[j].setVisited(false); } } } public int getAdjUnvisitedVertex(int v) { for (int k = 0; k < nVerts; k++) { if (adjMat[v][k] == 1 && vertexArray[k].isVisited() == false) { return k; } } return -1; } }
在图x中,遍历的顺序为:A -> B -> E -> F -> C -> D -> G -> H -> I
2)广度优先遍历
与深度优先相反,它首先访问起始顶点的所有邻接点,再一层一层地访问其它较远的顶点。
寻求两个顶点之间最短距离,可以使用广度优先遍历。
规则:
- 访问下一个未来访问的邻接点(如果存在),这个顶点必须当前顶点的邻接点,标记它,并把它插入队列中。
- 如果因为已经没有未访问的顶点而不能执行规则1,那么从队列头取一个顶点(如果存在),并使其成为当前顶点。
- 如果因为队列为空而不能执行规则2,则遍历结束。
public class Queue { private final int SIZE; private int[] queArray; private int front; private int rear; public Queue(int size) { this.SIZE = size; queArray = new int[SIZE]; front = 0; rear = -1; } public void insert(int d) { if (rear == SIZE - 1) { rear = -1; } queArray[++rear] = d; } public int remove() { int temp = queArray[front++]; if (front == SIZE) { front = 0; } return temp; } public boolean isEmpty() { return (rear + 1 == front) || (front + SIZE - 1 == rear); } }
public class Graph2 { private final int MAX_VERTS; private Vertex[] vertexArray; private int[][] adjMat; private Queue queue; private int nVerts; public Graph2(int verts) { this.MAX_VERTS = verts; vertexArray = new Vertex[MAX_VERTS]; adjMat = new int[MAX_VERTS][MAX_VERTS]; queue = new Queue(MAX_VERTS); nVerts = 0; } public void addVertex(char label) { vertexArray[nVerts++] = new Vertex(label); } public void addEdge(int start, int end) { adjMat[start][end] = 1; adjMat[end][start] = 1; } public void displayVertex(int index) { System.out.print(vertexArray[index].getLabel() + " -> "); } public int getAdjUnvisitedVertex(int v) { for (int k = 0; k < nVerts; k++) { if (adjMat[v][k] == 1 && vertexArray[k].isVisited() == false) { return k; } } return -1; } //breadth first search public void bfs() { vertexArray[0].setVisited(true); displayVertex(0); queue.insert(0); while (!queue.isEmpty()) { int r = queue.remove(); int v; while ((v = getAdjUnvisitedVertex(r)) != -1) { vertexArray[v].setVisited(true); displayVertex(v); queue.insert(v); } } for (int j = 0; j < MAX_VERTS; j++) { if (vertexArray[j] != null) { vertexArray[j].setVisited(false); } } } }
在图x中,遍历的顺序为:A -> B -> C -> D -> E -> F -> G -> H -> I




