概率论08 随机变量的函数
随机变量的函数
在前面的文章中,我先将概率值分配给各个事件,得到事件的概率分布。
通过事件与随机变量的映射,让事件“数值化”,事件的概率值转移到随机变量上,获得随机变量的概率分布。
我们使用随机变量的函数,来定制新的随机变量。随机变量的函数是从旧有的随机变量到一个新随机变量的映射。通过函数的映射功能,原有随机变量对应新的随机变量。通过原有随机变量的概率分布,我们可以获知新随机变量的概率分布。事件,随机变量,随机变量函数的关系如下:
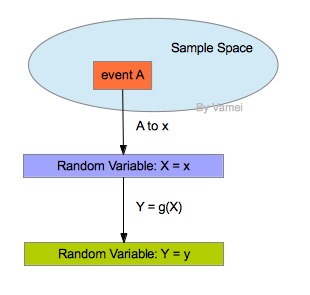
一个简单的例子是掷硬币。出现正面的话,我赢1个筹码,负面的话,我输1个筹码。那么,投掷一次,赢的筹码数是一个随机变量X,X可能取值为1和-1。因此X的分布为:
换一个角度来思考,我们将正负面“换算”成输赢的钱。如果一个筹码需要10元钱买,那么投掷一次硬币,赢的钱是一个随机变量Y,且Y=10X,Y的分布为:
Y实际上是随机变量X的一个函数。X的1对应Y的10,X的-1对应Y的-10。即Y=10X。
小总结,在上面的实验中,硬币为正面为一个事件。赢得的筹码数为一个随机变量X。赢得的钱是X的函数Y,它也是一个随机变量。
随机变量的函数还可以是多变量函数,。Y的值y对应的是多维空间的点
。比如掷硬币,第一次赢的筹码为
,第二次赢的筹码为
。我们可以构成一个新的随机变量
,即两次赢得的筹码的总和。
获得新概率分布的基本方法
一个核心问题是,如何通过X的概率分布,来获得 的概率分布。基本的思路是,如果我们想知道Y取某个值y的概率,可以找到对应的X值x的概率。这两个概率相等。
因此,我们使用如下方法来获得Y的概率。如果有函数关系,获得Y分布的基本方法是:
1. 通过找到对应
{Y≤y}的
区间I。
2. 在区间I上,积分,获得
P(Y≤y)。
3. 通过微分,获得密度函数。
如果有函数关系, 而X满足下面的分布:
对于任意
来说,
对上面的F(y)微分,即获得密度函数
绘制密度函数
上面的例子展示的是单变量函数,我们看一个多变量函数的例子。即 ,且已知
的联合分布为
。我们需要找到满足
的区间。
比如 ,且
满足如下分布:
为了让
,我们可以让
任意取值,而让
x2≤y−x1
让x_2 = v - x_1,有
微分,可得y的分布为:
上述方程也可以使用数值方法求解:

单变量函数的通用公式
上面求新的随机变量分布的步骤较为繁琐。在一些特殊情况下,我们可以直接代入通用公式,来获得新的分布。(通用公式实际上是从基本方法推导出的数学表达式)
对于单变量函数来说,如果 ,g是一个可微并且单调变化的函数 (在该条件,存在反函数
,使得
那么我们可以使用下面的通用公式,来获得Y的分布:
假设X为标准分布,即N(0,1),且
,那么
,因此:
可以看到,新的分布是一个μ=1,σ=5的正态分布,即N(1,5)
并不是所有的函数都有反变换,所以这里的“通用”公式并不能适用于所有的情况。
多变量函数的通用公式
在一些特殊情况下,我们可以使用多变量函数的通用公式。
如果 ,且存在反变换,使得
那么,我们可以通过如下公式,从X,Y的分布获得U,V的联合分布:
J表示雅可比变换(Jacobian tranformation),表示如下
如果X和Y是独立的随机变量,且有相同的分布。如果U=X+Y,V=Y,求U和V的联合分布。
由于X和Y独立,所以
根据U=X+Y,V=Y,可以得到, 且有:
Y=V
因此


