行列式（determinant）求值

如果A是一个矩阵（n*n方阵），则det(A)或| A |表示和A对应的n阶行列式，是一个标量。
行列式值直接求解（1阶行列式的值等于其唯一元素值）：

• 2阶矩阵的行列式：$\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} =a_{11} a_{22} - a_{12}a_{21}$

• 3阶矩阵的行列式：$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} =a_{11} a_{22} a_{33} + a_{12} a_{23} a_{31} + a_{13} a_{21} a_{32} - a_{13} a_{22} a_{31} - a_{11} a_{23} a_{32} - a_{12}a_{21}a_{33}$

---

代数余子式的概念：

n阶行列式中，位于第$i$行$j$列的元素$a_{ij}$，划去其所在的行和列，剩下的n-1阶行列式称为$a_{ij}$的余子式，余子式的值乘以$(-1)^{i+j}$就是$a_{ij}$的代数余子式的值。

代数余子式可以简化行列式值的求解，因为有如下定理：行列式的值等于，它其中任意行（或列）所有元素与其代数余子式乘积的和。

举例说明：

以下3阶行列式:

$\begin{vmatrix} 3 & 5 & 1 \\ 1 & 2 & 3 \\ 4 & 2 & 1 \end{vmatrix}$

其值为：$3*2*1+5*3*4+1*1*2-3*3*2-5*1*1-1*2*4 = 37$

若取最后一行元素（4、2、1）分解为代数余子式求解：
4的余子式为：

$\begin{vmatrix} 5 & 1 \\ 2 & 3 \end{vmatrix}$

4在第3行第1列（或第2行第0列，虽不影响结果，但行列式的行列都是从1开始数），所以代数余子式值为$(-1)^{3+1}*(5*3-1*2) = 13$
同理2和1的代数余子式值分别为-8、1。所以行列式的值为$4*13+2*(-8)+1*1 = 37$

---

行列式还有如下性质：

• 在行列式中，某一行（列）有公因子k，则可以提出k
  

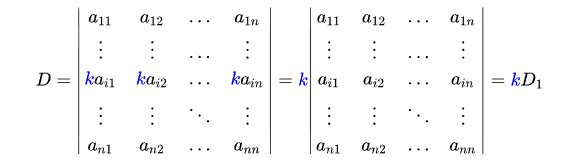
• 在行列式中，某一行（列）的每个元素是两数之和，则此行列式可拆分为两个相加的行列式
  

• 交换某两行（或两列）行列式值的符号改变。

• 行列式某一行（或列）元素全是0，则值为0。

• 行列式某一行（或列）乘以一个常数加到另一行（或列）上，行列式值不变。

---

利用最后一个性质可以简化行列式值求解（行列式值的简单求法）：

我们可以经过变换将行列式最后一行转化为只有最后一个元素不为0（只要用最后一列分别乘以某个数加到其他列上，总能把最后一行非末元素变为0的）。
然后利用行列式代数余子式展开求值法，可得此行列式值等于最后元素乘以其余子式的值。而其余子式也可以用以上方法进行变换，转化为最后行只有末元素不为零……
事实上，我们能够经过一系列转换，将行列式对角线下面的所有元素都转化为零，然后求值，这时候行列式的值等于位于其对角线上的所有元素的乘积。

下面的java程序递归实现了将行列式转为三角行列式（对角线下元素全为0）的步骤——

void setDet(double[][] det_, int k) {    //转换会改变参数det_，k为行列式的阶数。
    if(k == 1){
        return;
    }else{
        //如果行列式右下角元素为0，则通过减去一列保证其不为0
        if(det_[k-1][k-1] == 0){
            for(int j=0; j<k-1; j++){
                if(det_[k-1][j] != 0){
                    for(int i=0; i<k; i++){
                        det_[i][k-1] -= det_[i][j];
                    }
                    break;
                }
            }
        }
        
        double last = det_[k-1][k-1];
        for(int j=0; j<k-1; j++){
            double div = -det_[k-1][j] / last;
            for(int i=0; i<k; i++){
                det_[i][j] += div * det_[i][k-1];
            }
        }
        setDet(det_, k-1);
    }
}