数组题解

题目分类来源：https://leetcode-cn.com/circle/article/48kq9d/

---

 

数组的遍历

---

 

统计数组中的元素

645

 

697

点击查看关于map的总结

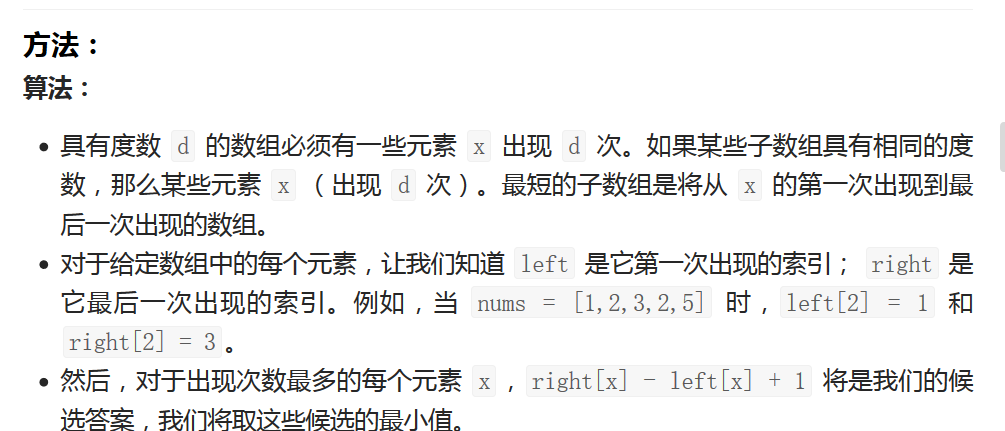
package Test;
import java.util.*;
public class Solution {
    //测试map的用法
    public static void test_Map() {

/*        格式：
        Map.getOrDefault(key，默认值)；

        Map中会存储一一对应的key和value。
        如果 在Map中存在key，则返回key所对应的的value。
        如果 在Map中不存在key，则返回默认值。*/
        Map<String,Integer>map=new HashMap<>();
        map.put("A", 11);
        map.put("B", 12);
        map.put("C",13);
        map.put("C",14);//更新了“C”对应的值
        Integer age=map.getOrDefault("C",30);
        System.out.println(age);
        age=map.getOrDefault("D",22);
        System.out.println(age);
        System.out.println(map.get("A"));//返回map中key对应的值
        System.out.println(map.get("E"));
        System.out.println(map.keySet());//返回map中所有key的列表
        for(String s:map.keySet()) {//迭代打印map中的key值
            System.out.println(s);
        }    
        System.out.println(map.values());//返回map中所有key对应的值列表
/*结果
14
22
11
null
[A, B, C]
A
B
C
[11, 12, 14]
*/
    }
    public static int findShortestSubArray(int[]nums) {
        if(nums==null|nums.length==0) return 0;
        if(nums.length==1) return 1;
        Map<Integer,Integer>l=new HashMap();//记录从左到右遍历数组每个元素第一次出现的位置
        Map<Integer,Integer>r=new HashMap();//记录从左到右遍历数组每个元素最后一次出现的位置
        Map<Integer,Integer>count=new HashMap();//记录元素和元素出现的次数，用来求“度”
        for(int i=0;i<nums.length;i++) {
            int x=nums[i];
            if(l.get(x)==null) l.put(x,i);
            r.put(x, i);
            count.put(x, count.getOrDefault(x, 0)+1);
        }
        int ans=nums.length;
        int degree=Collections.max(count.values());
        for(int x:count.keySet()) {
            if(degree==count.get(x)) {
                ans=Math.min(ans, r.get(x)-l.get(x)+1);
            }
        }
        return ans;
    }
    
    public static void main(String[] args) {
        int[]nums= {1,2,2,3,1,4,2};
        System.out.println(findShortestSubArray(nums));
        //test_Map();
    }
}

448

找到所有数组中消失的数字

给定一个范围在  1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组，数组中的元素一些出现了两次，另一些只出现一次。

找到所有在 [1, n] 范围之间没有出现在数组中的数字。

您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。

示例:

输入:
[4,3,2,7,8,2,3,1]

输出:
[5,6]

step1.暴力遍历 时间复杂度O(n**2)  空间复杂度O（1）

 对于[1,n]中的每一个数字，在目标数组中去找，如果没有找到就把它记录在list中，如果有则跳过。

static List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer>list=new ArrayList<>();
        for(int i=1;i<=nums.length+1;i++) {
            int flag=0;//假设当前数字没有出现在数组中
            for(int j=0;j<nums.length;j++) {
                if(i==nums[j]) {
                    flag=1;
                    break;
                }
            }
            if(flag==0) list.add(i);//如果没有出现就把这个数字存进list中
        }
        System.out.println(list.toString());
        return list;
    }

 

step2.使用额外空间 时间复杂度O(n)  空间复杂度O（n）

使用一个数组counter记录nums中每个元素出现的次数，再遍历数组counter找到所有元素值是0的元素的下标即可.

package Test;
import java.util.*;
public class Solution {
    static List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer>list=new ArrayList<>();
        int[]counter=new int[nums.length+1];//使用额外空间
        for(int i=0;i<nums.length;i++) {//记录nums中每个元素出现的次数
            counter[nums[i]]++;
        }
        for(int i=1;i<counter.length;i++) {
            if(counter[i]==0)
                list.add(i);
        }
        System.out.println(list.toString());
        return list;
    }
    
    public static void main(String[] args) {
        int[]nums= {4,3,2,7,8,2,3,1};
        findDisappearedNumbers(nums);
        
    }
}

 

step3.替换法

一般的替换步骤如下：
    //首先，题目就是要对比一个排序号的顺序序列，查看哪些没出现，所以直接将两个数组摆出来：
    //4,3,2,7,8,2,3,1  数组1
    //1,2,3,4,5,6,7,8  数组2
    //上面是原数组，下面是序列数组；
    //遇到上面的数字，就将数组2中同样数字给替换为：替换字符（随便设置，这里可以设为*），意思就是该数字已经出现过了；
    //这样不断对照查找哪些元素出现过；则没被替换的就是没出现过的；
    //这基本是最基本的逻辑；

    //4,3,2,7,8,2,3,1
    //依次类推替换
    //1,2,3,*,5,6,7,8
    //1,2,*,*,5,6,7,8
    //1,*,*,*,5,6,7,8
    //1,*,*,*,5,6,*,8
    //1,*,*,*,5,6,*,*
    //1,*,*,*,5,6,*,*  位置2已经替换过,不用再替换；
    //1,*,*,*,5,6,*,*  位置3已经替换过,不用再替换；
    //*,*,*,*,5,6,*,*  此时5，6没被替换，说明5，6在数组1中没出现过；
    //但这样的替换需要额外用一个序列数组（1到n)，
    //所以才有用自身数组元素的负数作为替换字符的方法，这样被替换字符也可以继续作为索引值使用；节省了一个数组空间；

思路：将所有正数作为数组下标，置对应数组值为负值。那么，仍为正数的位置即为（未出现过）消失的数字。

举个例子：
    原始数组：[4,3,2,7,8,2,3,1]
    重置后为：[-4,-3,-2,-7,8,2,-3,-1]
    [8,2] 分别对应的index为[5,6]（消失的数字）

class Solution {
    public List<Integer> findDisappearedNumbers(int[] nums) {
        List<Integer>r=new ArrayList<>();
        for(int i=0;i<nums.length;i++){
            if(nums[Math.abs(nums[i]) - 1]>0){
                nums[Math.abs(nums[i])-1]=-nums[Math.abs(nums[i])-1];
            }
        }
        for(int i=0;i<nums.length;i++){
            if(nums[i]>0){
                r.add(i+1);
            }
        }
        return r;
    }
}

442

思路:    找到数字i时，将位置i-1处的数字翻转为负数。 如果位置i-1 上的数字已经为负，则i是出现两次的数字。

package Test;
import java.util.*;
public class Solution {
    
    public static List<Integer>findDuplicates(int[] nums){
        List<Integer>r=new ArrayList<>();
        for(int i=0;i<nums.length;i++) {
            int index=Math.abs(nums[i])-1;
            if(nums[index]<0) {
                r.add(Math.abs(index+1));
            }
            if(nums[index]>0) {
                nums[index]=-nums[index];
            }
        }
        return r;
    }
    
    public static void main(String[] args) {
        int[]nums= {4,3,2,7,8,2,3,1};
        List<Integer>list=findDuplicates(nums);
        System.out.println(list.toString());
    }
}

 

 

41

package Test;
import java.util.*;
public class Solution {
    //method1 首先最容易想到的就是暴力求解，从1开始一个个查找，没找到就直接返回
/*    复杂度分析：
    时间复杂度：O(N*N)
          空间复杂度：O(1)
*/    
    public static int findMissingPositive0(int[]nums) {
        System.out.println(Arrays.toString(nums));
        for(int i=1;i<nums.length+1;i++) {
            int flag=0;//flag==0表示假设当前这个数没有出现
            for(int j=0;j<nums.length;j++) {
                if(nums[j]==i) {
                    flag=1;
                    break;
                }
            }
            if(flag==0) return i;
        }
        return nums.length+1;
    }
    
    //method2 先排序，再二分查找
/*    复杂度分析：
    时间复杂度：O(N*log(N)。时间复杂度主要消耗在排序上，排序使用 O(N*log⁡N)。二分查找使用每一步使用的时间复杂度是 O(log⁡N)，整体上仍然是 O(Nlog⁡N)
          空间复杂度：O(1)
*/
    public static int BS(int[]nums,int t) {
        int l=0,r=nums.length-1;
        while(l<=r) {
            int mid=l+(r-l)/2;
            if(nums[mid]==t) return mid;
            else if(nums[mid]<t)
                l=mid+1;
            else r=mid-1;
        }
        return -1;
    }
    public static int findMissingPositive1(int[] nums){
        int len=nums.length;
        Arrays.sort(nums);
        System.out.println(Arrays.toString(nums));
        for(int i=1;i<len+1;i++) {
            int res=BS(nums,i);
            if(res==-1) return i;
        }
        return len+1;
    }
    //method3 把原数组的值全部存放到集合set中，然后再从1开始循环，判断这个数是否存在集合中，如果不存在直接返回
/*    复杂度分析：
    时间复杂度：O(N)，这里 N 表示数组的长度。第 1 次遍历了数组，第 2 次遍历了区间 [1, len] 里的元素。
          空间复杂度：O(N)，把 N 个数存在哈希表里面，使用了 N个空间。
*/
    public static int findMissingPositive2(int[] nums) {
        Set<Integer>hashset=new HashSet<>();
        for(int num:nums) {
            hashset.add(num);
        }
        for(int i=1;i<nums.length;i++) {
            if(!hashset.contains(i))
                return i;
        }
        return nums.length+1;
    }
    //method4 把数组元素存在对应的位置上(将数组视为哈希表)
/*    那就是数值为 i 的数映射到下标为 i - 1 的位置.比如1存放到数组的第一个位置，3存放到数组的第3个位置.
    遍历一次数组把大于等于1的和小于数组大小的值放到原数组对应位置
    然后再遍历一次数组查当前下标是否和值对应，如果不对应那这个下标就是答案
                                         否则遍历完都没出现那么答案就是数组长度加1。
*/
/*    复杂度分析：
    时间复杂度：O(N)，这里 N 表示数组的长度。
          空间复杂度：O(1)
*/
    public static void swap(int[]A,int i,int j) {
        if(i!=j) {
            int tmp=A[i];A[i]=A[j];A[j]=tmp;
        }
    }
    public static int findMissingPositive3(int nums[]) {
        for (int i = 0; i < nums.length; i++) {
            //如果在指定的位置就不需要修改
            if (i + 1 == nums[i])
                continue;
            int x = nums[i];
            if (x >= 1 && x <= nums.length && x != nums[x - 1]) {
                swap(nums, i, x - 1);
                i--;//抵消上面的i++，如果交换之后就不++；
            }
        }
        //最后在执行一遍循环，查看对应位置的元素是否正确，如果不正确直接返回
        for (int i = 0; i < nums.length; i++) {
            if (i + 1 != nums[i])
                return i + 1;
        }
        return nums.length + 1;     //都正确则返回数组长度 + 1
    }
    public static void main(String[] args) {
        int[]nums= {7,8,9,11,12,4};
//        System.out.println(findMissingPositive0(nums));
//        System.out.println(findMissingPositive1(nums));
//        System.out.println(findMissingPositive2(nums));
        System.out.println(findMissingPositive3(nums));
    }
}

 

274

 453

665

package Test;
import java.util.*;
public class Solution {
    public static int[] twoSum1(int[] nums, int target) {
        for(int i=0;i<nums.length;i++) {
            for(int j=i+1;j<nums.length;j++) {
                if(target-nums[j]==nums[i]) {
                    return new int[] {i,j};
                }
            }
        }
        return new int[] {};

    }
    public static int[] twoSum2(int[] nums, int target) {
        Map<Integer,Integer>map=new HashMap<>();
        for(int i=0;i<nums.length;i++) {
            map.put(nums[i], i);
        }
        for(int i=0;i<nums.length;i++) {
            int r=target-nums[i];
            if(map.containsKey(r)&&map.get(r)!=i) {
                return new int[] {i,map.get(r)};
            }
        }
        return new int[] {};
    }
    public static int[] twoSum3(int[] nums, int target) {
        Map<Integer,Integer>map=new HashMap<>();
        for(int i=0;i<nums.length;i++) {
            int r=target-nums[i];
            if(map.containsKey(r)) {
                return new int[] {map.get(r),i};
            }
            map.put(nums[i],i);
        }
        return new int[]{};
    }
    public static void main(String[] args) {
        int[]nums= {2,7,11,15};
        int target=9;
        System.out.println(Arrays.toString(twoSum3(nums,target)));
        
    }
}

 118

package Test;
import java.util.*;
public class Solution {
    public static List<List<Integer>> generate(int n) {
        List<List<Integer>>list=new ArrayList<List<Integer>>();
        if(n==0) return list;
        int [][]array=new int[n][n];
        
        for(int i=0;i<n;i++) {
            List<Integer>tmp=new ArrayList<>();
            for(int j=0;j<=i;j++) {
                if(j==0||j==i) {
                    array[i][j]=1;
                }else if(i>=1) {
                    array[i][j]=array[i-1][j]+array[i-1][j-1];
                }
                tmp.add(array[i][j]);
            }
            list.add(tmp);
        }
        return list;
    }
    public static void main(String[] args) {
        int n=5;
        for(List<Integer>list:generate(n)) {
            System.out.println(list);
        }
        
        
    }
}

661

1.递推法
求出全部的值放在列表里，查找即可
2.公式法
如果输入的行数是n，那么该行内容依次是：1、(n-1)/1、(n-1)(n-2)/2、(n-1)(n-2)(n-3)/3...

class Solution {
    public List<Integer> getRow(int rowIndex) {
            List<Integer> pre = new ArrayList<>();
            List<Integer> cur = new ArrayList<>();
            for (int i = 0; i <= rowIndex; i++) {
                cur = new ArrayList<>();
                for (int j = 0; j <= i; j++) {
                    if (j == 0 || j == i) {
                        cur.add(1);
                    } else {
                        cur.add(pre.get(j - 1) + pre.get(j));
                    } 
                }
                pre = cur;
            }
        return cur;
    }
}