B-树木（B树）和B+树

1.B-树（B树）的性质

B-树又称为B树，他们是一个东西。

介绍B-树之前，首先看一下一个重要的概念：阶。

一个树的阶，就是这个树中各个节点的子树个数的最大值。也就是说，如果有的节点有2个子节点，有的节点有4个子节点，最多的有5个子节点，那么，这个树的阶就是5.从这个角度来讲，二叉树的阶是2.

性质：

1，每个节点最多有m个子节点。最少有m/2（向上取整）个子节点。或者这么表述：m/2 <= 子节点个数<= m。但是根节点是例外的，根节点可以最少有2个子节点。

2，每个节点的子节点的个数，比该节点中保存的关键字的个数多1. 也就是，当节点中保存k个关键字时，该节点会有k + 1个子节点（子树）。

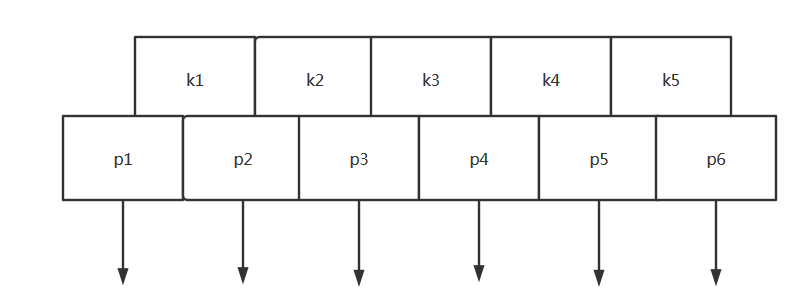
3，每个节点中的k个关键字是按照从小到到排列的，分别记为k1，k2，k3，......kk。那么该节点会有k+1个指针，记为p0，p1，p2，......pk。并且，p3所指向的子节点中的所有元素，都大于k3，且都小于k4. 如下图所示。这一点也比较容易理解和记忆，各个指针p整好位于关键字k的插空的位置，所以，插空处的指针指向的子节点的元素的值，就理所当然的应该大于指针左边的元素，小于指针右边的元素。

4，B-树是严格的平衡查找树，它的左右子树的高度是相等的。且叶子节点处于同一层，并且可以用空节点表示。

一个B-树的例子：

 

 

 

 

 

 

 

2..B-树查找

B-树的查找是二叉排序树查找的扩展，二叉排序树是二路查找，B-树是多路查找，因为B-树结点内的关键字是有序的，在结点内进行查找时除了顺序查找外，还可以用折半查找来提升效率。B-树的具体查找步骤如下（假设查找的关键字为key）：
1）先让key与根结点中的关键字比较，如果key等于k[i]（k[]为结点内的关键字数组），则查找成功
2）若key<k[1]，则到p[0]所指示的子树中进行继续查找（p[]为结点内的指针数组），这里要注意B-树中每个结点的内部结构。
3）若key>k[n]，则道p[n]所指示的子树中继续查找。
4）若k[i]<key<k[i+1]，则沿着指针p[I]所指示的子树继续查找。
5）如果最后遇到空指针，则证明查找不成功。

 

3.B-树插入

插入过程和树的构建过程本质是一致的，即都是进行插入操作，并对插入后的B-树进行调整。

我们设定B-树的阶为5。用关键字序列{1,2,6,7,11,4,8,13,10,5,17,9,16,20,3,12,14,18,19,15}来构建一棵B-树。

因为树的阶为5，那么，每个节点最多有5个子节点，每个节点内的关键字个数为2~4个。

step1　插入1，2，6，7作为一个节点。然后插入11，得到1，2，6，7，11. 因为节点个数超过4，所以需要对该节点进行拆分。选取中间节点6，进行提升，提升为父节点，于是得到：

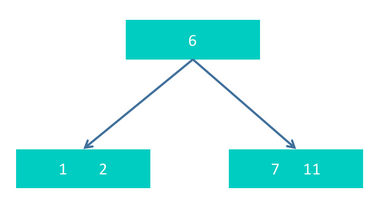
有一个规则是新插入的节点总是出现在叶子节点上，

step2　　插入4，8，13，直接插入得到

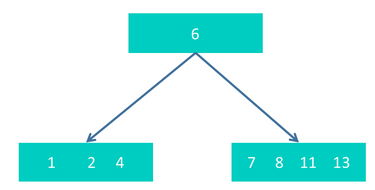
step3　　插入10. 得到

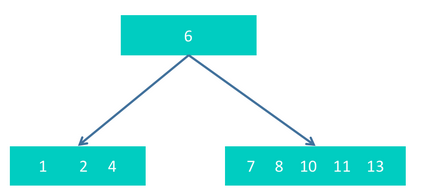
因为最右下的节点内有5个元素，超过最大个数4了，所以需要进行拆分，把中间节点10进行提升，上升到和6一起，形成如下结构

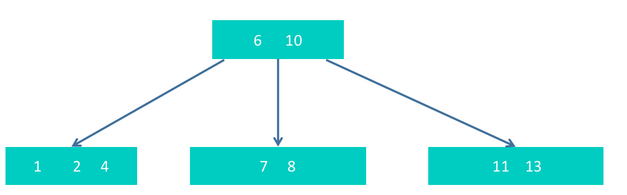
step4　　插入5，17，9，16，得

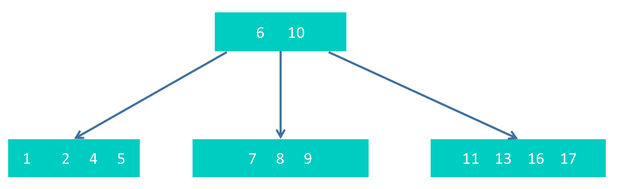
step5　　插入20，插入20后，最右下节点内元素个数为5个，超过最大个数4个，所以，需要把16进行提升，形成如下结构

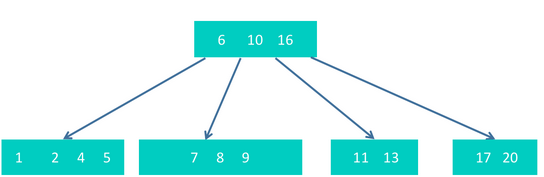
step6　　插入3、12、14、18、19，后，形成如下结构

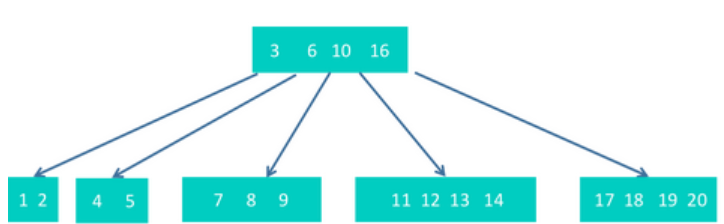
step7　　插入15

会导致13提升到根节点，这时，根节点会有5个节点，那么，根节点中的10会再次进行提升，形成如下结构。

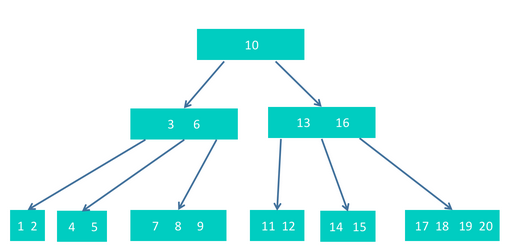
结束。

 4.B-树的删除

对于B-树关键字的删除，需要找到待删除的关键字，在结点中删除关键字的过程也有可能破坏B-树的特性，如旧关键字的删除可能使得结点中关键字的个数少于规定个数。在B-树中删除节点时，可能会发生向兄弟节点借元素、孩子节点交换元素、节点合并的操作。

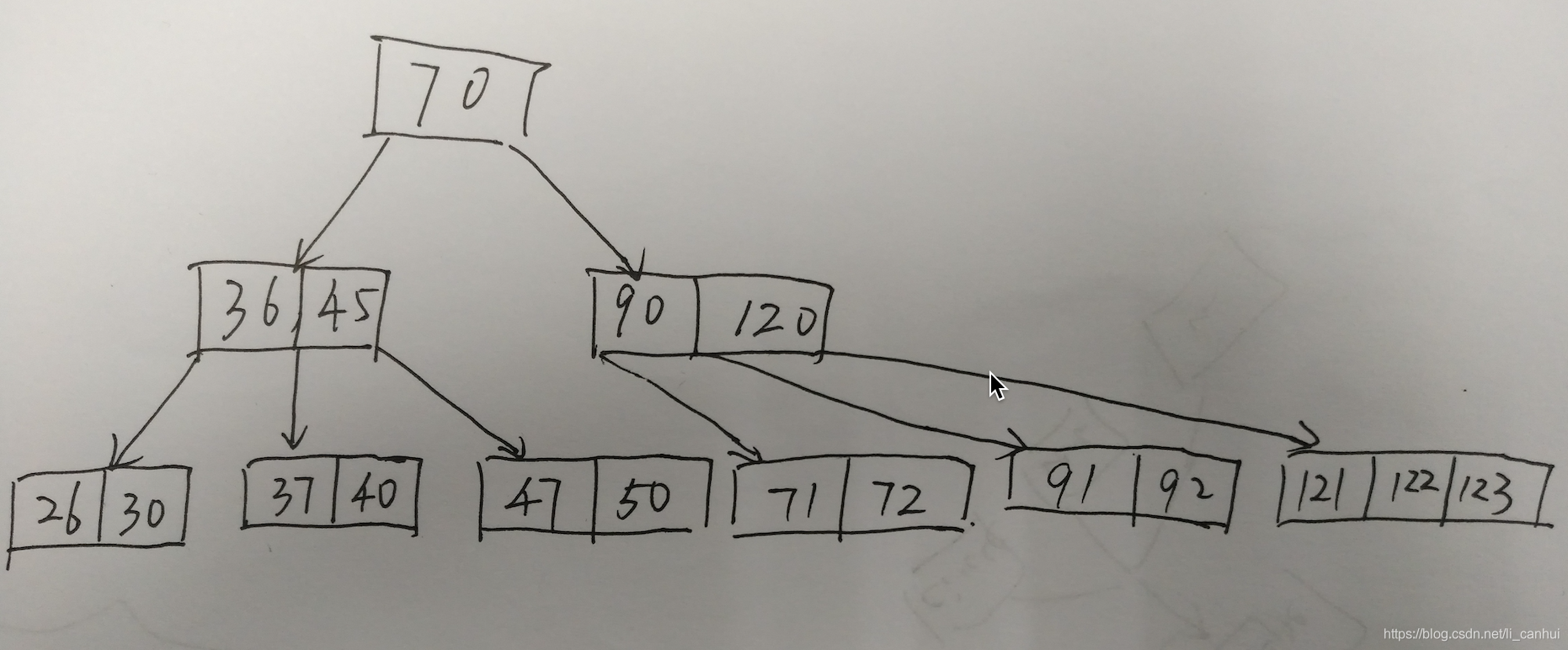
我们以下面的树为基础，进行删除操作。

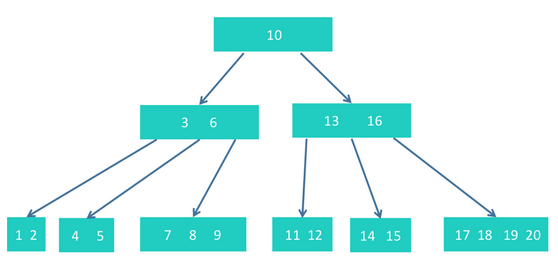
首先明确一下这个树的定义。它是一个5阶树。所以，每个节点内元素个数为2~4个。

我们依次删除8、16、15、4这4个元素。

step1　　首先删除8，因为删除8后，不破坏树的性质，所以直接删除即可。得到如下

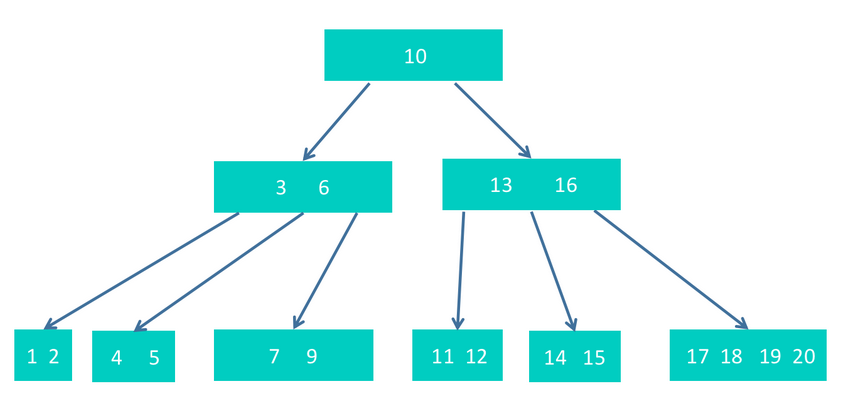
step2　　然后删除16，这导致该节点只剩下一个13节点，不满足节点内元素个数为2~4个的要求了。所以需要调整。这里可以向孩子借节点，把17提升上来即可，得到下图。这里不能和兄弟节点借节点，因为从3，6节点中把6借走后，剩下的3也不满要求了。另外，也不能把孩子中的15提升上来，那样会导致剩下的14不满足要求。

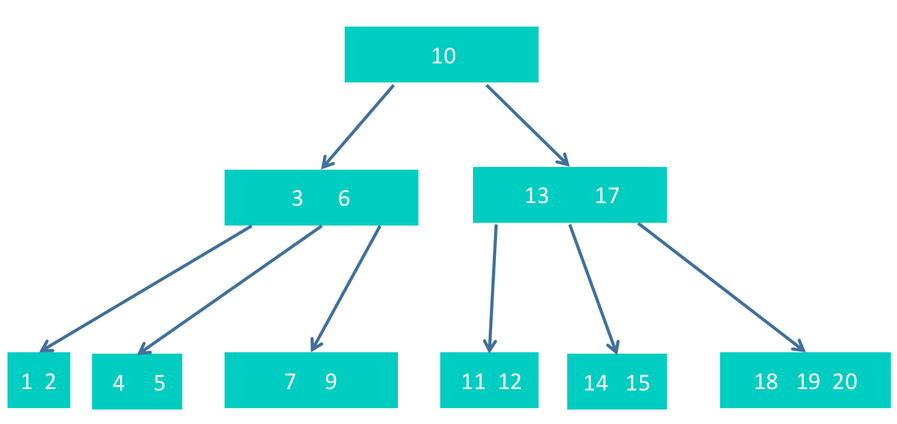
step3　　然后删除15，删除15后同样需要调整。调整的方式是，18上升，17下降到原来15的位置，得到下图。

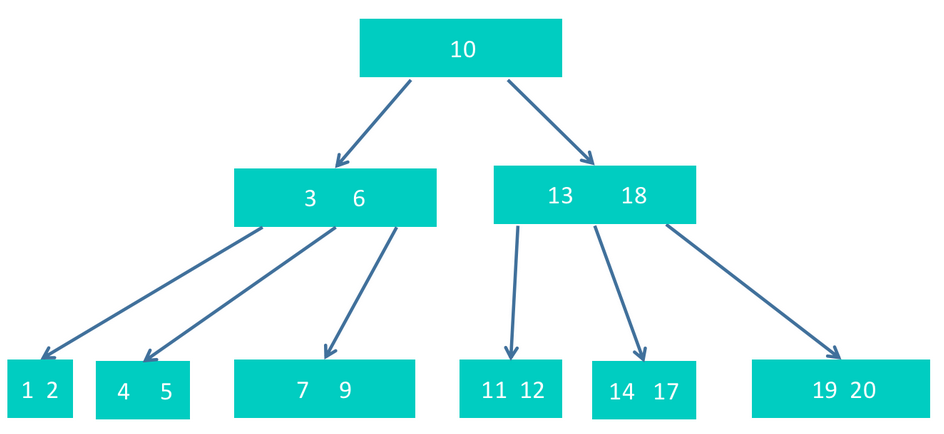
step4　　然后删除元素4，删除4后该节点只剩下5，需要调整。可是它的兄弟节点也都没有多余的节点可借，所以需要进行节点合并。节点合并时，方式会有多种，我们选择其中的一种即可。这里，我们选择父节点中的3下沉，和1，2，以及5进行合并，如下图。

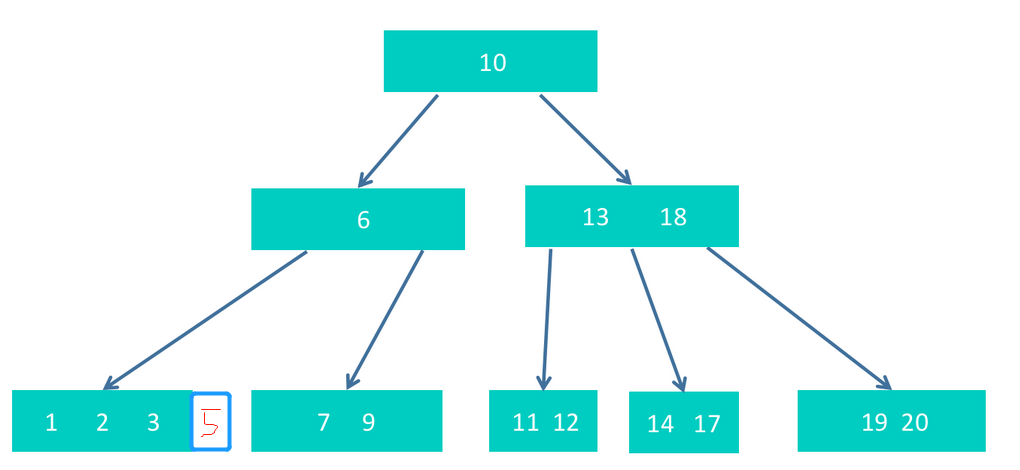
但这次调整，导致6不符合要求了。另外，6非根节点，但只有2个孩子，也不符合要求。需要继续调整。调整的方式是，将10下沉，和6，以及13，18合并为根节点，如下图。

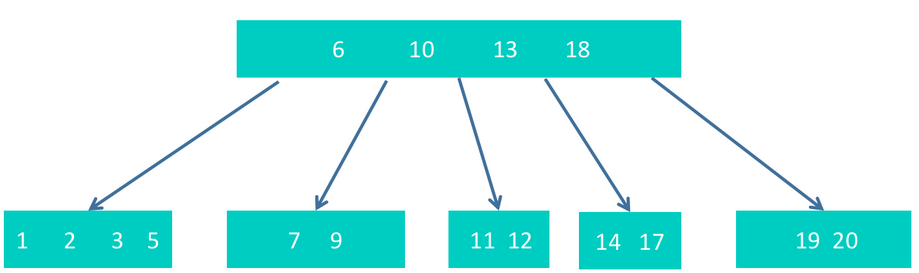
 结束。

5.B+树

参考1

6.一些面试问题

1，那么B+树和B树的区别是什么呢？

B+数是从B树改进来的，它和B树的主要区别在于，B+树中保存元素的节点都位于叶子节点，非叶子节点只起到索引的作用。而且，B+树不同子树直接有指针连接起来了。

2，数据库的索引一般采用B+树来实现，可以达到的时间复杂度为log(n)。更进一步讨论这个问题，如果我们用hash表来保存索引，那么时间复杂度可以达到O(1)。既然用哈希表保存索引比B+树效率更高，那为什么不用哈希表来实现数据库的索引呢？这主要是考虑数据量的问题。数据库的索引是保存在磁盘上的，如果数据量太大，那么就没有办法一次都载入内存。

3，关于B树，B树是一个多路排序树，为什么要设计成多路的呢？

是为了进一步降低树的高度，提高查找效率。在极端情况下，把多路定位无限多，那么B树会变成一个有序数组。

B树一般用在文件系统索引上。文件系统索引为什么喜欢用B树，而不用红黑树或有序数组呢？这是因为，文件系统的索引都是保存在磁盘上的，如果数据量特别大的话，不一定能够一次都载入到内存中。我们可以每次只加载B树的一个节点进行查找。

4，为什么B+树的叶子节点要用指针连接起来？
这个是和业务场景有关的。B+树常用来保存数据库索引，数据库select数据，不一定只选一条，很多时候会选多条。如果选多条的话，B树需要进行局部的中序遍历，才能获取到所有符合条件的元素，而且很可能要跨层访问。而B+树因为所有元素都在叶子节点上，且不同子树的叶子节点已经用指针连接起来了，当需要选择多条数据时，B+树就会有很大的优势。

 

参考：https://www.jianshu.com/p/7dedb7ebe033；https://blog.csdn.net/li_canhui/article/details/85307195