作业五 线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

自己理解：对一些数据源，特别是数据源是连续型变量，离散变量，对温度的回归预测，对天气的走向。对已有的数据来预测下一次数据的走向。在线性回归中，数据使用线性预测函数来建模，并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。最常用的线性回归建模是给定X值的y的条件均值是X的仿射函数。

研究一个自变量(X)和一个因变量（y）的关系

       简单线性回归模型定义：

 

 

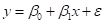
         简单线性回归方程：

 

 

 

　　其中：

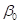　　为回归线的截距

　　 为回归线的斜率

　　通过训练数据，求取出估计参数建立的直线方程：

 

 

 

线性回归重点：

 

 

 

 

 

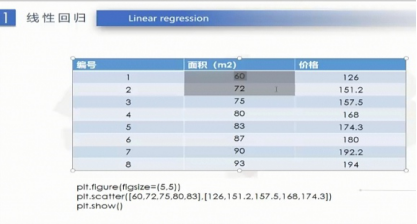
预测之后有误差，利用最小二乘法来减少误差。

 

 

 

2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）

由于现在疫情影响，数据的支撑在一定程度上大大让很多专家来预测下一步的疫情走向，来进行下一步的防御措施。

线性回归还可以帮助农民在一定的季度种植一些可以卖出很好价值的瓜果蔬菜，通过很多数据的显示，在一定程度上，农民可以选择下一年自己要种植市场需要的东西。

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

import numpy as np
from matplotlib import pylab as pl

# 定义训练数据
x = np.array([1,3,2,1,3])
y = np.array([14,24,18,17,27])

# 回归方程求取函数
def fit(x,y):
    if len(x) != len(y):
        return
    numerator = 0.0
    denominator = 0.0
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    for i in range(len(x)):
        numerator += (x[i]-x_mean)*(y[i]-y_mean)
        denominator += np.square((x[i]-x_mean))
    b0 = numerator/denominator
    b1 = y_mean - b0*x_mean
    return b0,b1

# 定义预测函数
def predit(x,b0,b1):
    return b0*x + b1

# 求取回归方程
b0,b1 = fit(x,y)
print('方程是:y = %2.0fx + %2.0f'%(b0,b1))

# 预测
x_test = np.array([0.5,1.5,2.5,3,4])
y_test = np.zeros((1,len(x_test)))
for i in range(len(x_test)):
    y_test[0][i] = predit(x_test[i],b0,b1)

# 绘制图像
xx = np.linspace(0, 5)
yy = b0*xx + b1
pl.plot(xx,yy,'k-')
pl.scatter(x,y,cmap=pl.cm.Paired)
pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
pl.show()

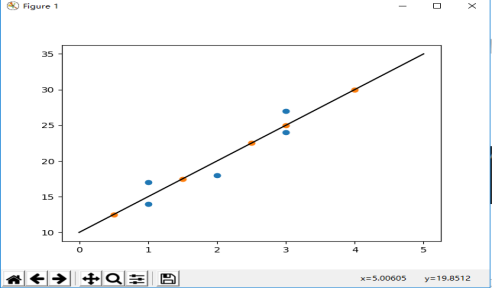
截图如下：