2020软件工程作业04

|这个作业属于哪个课程| https://edu.cnblogs.com/campus/zswxy/2018SE/|
|----|----|----|
|这个作业要求在哪里| https://edu.cnblogs.com/campus/zswxy/2018SE/homework/11406/|
|这个作业的目标| 寻找数组中第K大是哪个数 二叉树的先、中、后 序遍历与层级遍历|
|学号| 20189744|
|其他参考文献| b站，百度，博客园|

题目一：寻找数组中第K大是数 考察算法：排序算法
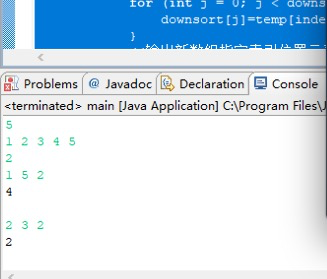
解题思路：对这个乱序数组按照从大到小先行排序，然后取出前k大，总的时间复杂度为O(n*logn + k)。
代码

package zy;
import java.util.Arrays;
import java.util.Scanner;
public class main{
 public  static void main(String[] args) {
  Scanner sc = new Scanner(System.in);
  int n =sc.nextInt();
  int arr[] = new int[n];
  for (int i = 0; i < arr.length; i++) {
   arr[i] = sc.nextInt();//给定的序列
  }
  int p = sc.nextInt();//输入询问个数
  for (int i = 0; i < p; i++) {
   int l = sc.nextInt();
   int r = sc.nextInt();
   int k = sc.nextInt();//输入指定K
   int temp[] = new int[r-l+1];
   int index=0;
   //将指定范围元素赋给新的数组
   for (int j = l-1; j <= r-1; j++) {
    temp[index++]=arr[j];
   }
   Arrays.sort(temp);//指定范围元素的新数组进行排序
   int downsort[] = new int[temp.length];
   int index2 = temp.length-1;
   //按照倒叙的方式赋予下一个新数组
   for (int j = 0; j < downsort.length; j++) {
    downsort[j]=temp[index2--];
   }
   //输出新数组指定索引位置元素
   System.out.println(downsort[k-1]);
  }
 }
}

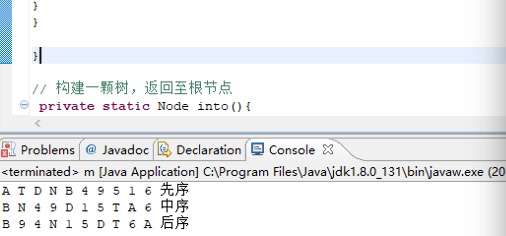
题目二：二叉树的先、中、后 序遍历与层级遍历
解题思路：
先序遍历：第一次经过这个结点的时候访问。
中序遍历，第二次经过这个结点的时候访问了结点，就是从左孩子返回的这个箭头的时候访问。
后序遍历，第三次经过这个结点的时候访问。就是从右孩子返回的这个箭头的时候访问。
层序遍历，按照一层一层的顺序，从左到右。

package zy;

import java.util.LinkedList;

public class m {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		/*
        作业要求：叉树的先、中、后 序遍历与层级遍历
        自己实现四个方法，Tree01方法中调用，将结果打印到控制台
     */
		 /*  二叉树的结构
        A
       / \
      T   6
     /
    D
  /   \
 N     5
/ \    /
B   4  1
    \
     9
*/
 Node root = into();
// 先序遍历
 A(root);
 System.out.println("先序");
// 中序遍历
 B(root);
 System.out.println("中序");
// 后序遍历
 C(root);
 System.out.println("后序");
// 层级遍历
 D(root);
 System.out.println("层级");

}
 private static void A(Node tree) {
// TODO 先序遍历
 if (tree != null) {
   System.out.print(tree.data + " ");
   A(tree.l);
   A(tree.r);
}

}

 private static void B(Node tree) {
// TODO 中序遍历
 if (tree != null) {
 B(tree.l);
 System.out.print(tree.data + " ");
 B(tree.r);
}

}

 private static void C(Node tree) {
// TODO 后序遍历
 if (tree != null) {
 C(tree.l);
 C(tree.r);
 System.out.print(tree.data + " ");
}

}

 private static void D(Node tree) {
// TODO 层级遍历
 if (tree != null) {
 LinkedList<Node> linkedList = new LinkedList<Node>();
     //将根节点列入到List中
 linkedList.offer(tree);
 Node node = null;
 while (!linkedList.isEmpty()) {
	 //移除列表中的一个元素,返回元素值
   node = (Node) linkedList.pop();
   System.out.print(node.data + " ");
   if (node.l != null) {
       //将出队结点的左子树根入队
       linkedList.offer(node.l);
   }
   if (node.r != null) {
       //将出队结点的右子树根入队
       linkedList.offer(node.r);
   }
}
}

}

// 构建一颗树，返回至根节点
 private static Node into(){
 Node root = new Node("A");
 Node node1 = new Node("T");
 Node node2 = new Node("D");
 Node node3 = new Node("N");
 Node node4 = new Node("B");
 Node node5 = new Node("6");
 Node node6 = new Node("5");
 Node node7 = new Node("4");
 Node node8 = new Node("9");
 Node node9 = new Node("1");
 root.l = node1;
 node1.l = node2;
 node2.l = node3;
 node2.r = node6;
 node3.r = node7;
 node7.r = node8;
 node6.l = node9;
 node3.l = node4;
 root.r = node5;
 return root;
}

// 节点
 static class Node{
// 数据
 Object data;
// 左孩子
 Node l;
// 右孩子
 Node r;

 public Node(){}

 public Node(Object data) {
 this.data = data;
 this.l = null;
 this.r = null;
}

 public Node(Object data, Node l, Node r) {
 this.data = data;
 this.l = l;
 this.r = r;
}
	}

}