Transforrmer的时间序列模型
1、它利用输入嵌入中添加的位置编码来模拟序列信息。(位置编码)
绝对位置编码:

t表示位置索引,w为每个维度的频率信息
相对位置编码:根据输入元素之间的成对位置关系比元素的位置更有利的直觉,相对位置编码方法已经被提出。例如,其中一种方法是将可学习的相对位置嵌入到注意力机制的关键中
混合位置编码:将两种方法结合起来。位置编码被添加到标记嵌入中,并送入转化器
2、注意力机制
2.1Attnention原理
在对于各时序点数据重视程度是一样的,而注意力机制在Decoder端使用针对不同解码值使用不同中间语义表示向量Ci,可理解为,在解码器计算相应yi时,使用不同针对编码器不同中间语义值Ci

Attnetion主要使用由三个部分组成:
第一个是Query,可视作时序数据中每个词向量对应的查询向量,其所构成的张量维度为[batch size, Target sequence length, (h, 使用多头方法时的多头数目), hidden embedding dimension (/h, 使用多头时应除以多头数目];
第二个是Key,可视作时序数据中每个词向量对应的键值向量,其所构成的张量维度为[batch size, Source sequence length, (h, 使用多头时多头数目), hidden embedding dimension (h, 使用多头时应除以多头数目],Key与各词向量对应的键向量相乘后再进行softmax可以得到注意权重值。
第三个是Value,可视作时序数据中每个词向量对应的隐藏信息,其所构成的张量维度为[batch size, Source sequence length, (h, 使用多头时多头数目), Output embedding dimension (h, 使用多头时应除以多头数目]。
缩放点乘法注意力
因此Attention的计算步骤主要有两步:1、求权重系数2、求Attention 的值
1、根据当前Query与各Key计算得到相关性评价值,得到一阶的相关程度值矩阵,其中通常评价相关性值的方法主要有三种,一是求两个向量点积;二是求cos的相似性;三是利用神经网络求解;四是加和等方法
再对矩阵中的各值进行归一化处理,得到各Value对应的注意力权重值a,通常采用Softmax方法。
2、用注意力权重a与Source中的Value进行加权求和,得出注意力值Attention。
具体算例如下:
设Query为M ×d,其中M为Source时序数据长,Key为为N ×d,其中N为Target时序数据长,d为向量维度。可见,向量Q与K是等长的,因为两者应在同一个维度空间中,需要进行相似度比较,即dQ = dK= d。但V为N ×dv,其向量长度可与两者不同,可以认为K与V的键值对是在不同状态空间中对同一数据的表示,最终Attention值为M ×dv的矩阵,使用Softmax加权后得到权重系数,依据系数在dv个维度上进行加权求和,最终得出M个具有dv维度的Attention值。

2.2多头注意力
Attention是将query和key映射到同一高维空间中去计算相似度,而对应的multi-head attention把query和key映射到高维空间的不同子空间中去计算相似度

2.3自注意力
跳脱出了Source与Target的框架,而是寻找Source或Target内部的注意力机制。Self-Attention中的Q、K、V均为相同输入,其计算方式仍与Attention方法相同,encoder中的self-attention的query, key, value都对应了源端序列(即A和B是同一序列),decoder中的self-attention的query, key, value都对应了目标端序列
通过计算Self-Attention,可以分析时序数据中内部信息的关系
举例:求解得到句子中各单词对当前解码单词的贡献程度,可以表示一个句子中每个单词之间的依赖关系。时间序列预测中采用给注意力机制

2.4 时序预测中的注意力机制
2.4.1 informer概率稀疏注意力
(KL散度进行注意力区分,通过关注TOP-U个占据主导位置的query来实现)
论文标题:Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting
论文链接:
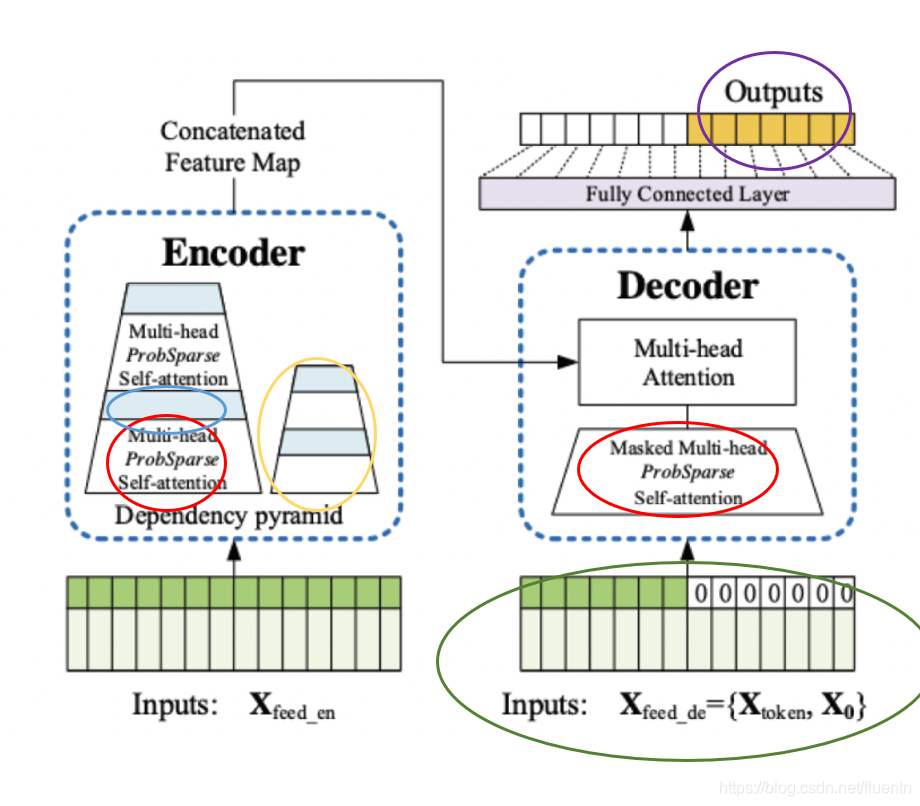
Transformer在长距离依赖的表达方面表现出了较高的潜力。然而,Transformer存在几个严重的问题,使其不能直接适用于LSTF问题,例如、高内存使用量和编码器-解码器体系结构固有的局限性。其中Transformer模型主要存在下面三个问题:
-
self-attention机制的二次计算复杂度问题:self-attention机制的点积操作使每层的时间复杂度和内存使用量为 。
-
高内存使用量问题:对长序列输入进行堆叠时,J个encoder-decoder层的堆栈使总内存使用量为 ,这限制了模型在接收长序列输入时的可伸缩性。
-
预测长期输出的效率问题:Transformer的动态解码过程,使得输出变为一个接一个的输出,后面的输出依赖前面一个时间步的预测结果,这样会导致推理非常慢。
主要是为解决self-attention机制的过度使用采用概率稀疏的注意力来替代,
ProbSparse Self-attention 输入: 32 × 8 × 96 × 64 (8×64=512 ,这也是多头的原理,即8个头) 输出:32 × 8 × 25 × 64
我们回顾了传统的注意力机制,引入了注意力概率矩阵,下面直接进入到最精彩的部分——ProbSparse的注意力机制。
对原始的注意力机制进行改写,进行一步对注意力进行区分:分为Activate-lazy 两种,通过KL散度(信息熵来划分两种注意力),利用建立的度量标准,通过TOP-U个占据主导地位的query,最终实现概率稀疏注意力(实际上也是比较合理的,因为某个元素可能之和几个元素高度相关,其他的并无显著关联)。基于这样的结果,引入了attention:

主要公式为:


2.4.2 STTNs动态空间注意力
(联合利用动态的定向空间依赖和长距离的时间依赖来提高长期交通流预测的准确性。我们提出了一种新的图神经网络变体,名为空间Transformer,以动态的方式建立具有自注意力机制的有向空间依赖关系模型,以捕捉交通流的实时状况和方向)
论文标题:Spatial-Temporal Transformer Networks for Traffic Flow Forecasting
论文链接:[
-
交通流具有高度的非线性和动态的时空相关性,如何实现及时准确的交通预测,特别是长期的交通预测仍然是一个开放性的挑战
-
提出了一种新的Spatio-Temporal Transformer Network(STTNs)范式,该范式联合使用 dynamical directed spatial dependencies和long-range temporal dependencies来提高长期交通流预测的准确性。
-
Spatial transformer利用self-attention对有向空间依赖关系进行动态建模,以捕获交通流的实时状态和方向。并且考虑了相似性、连通性和协方差等多种因素,采用multi-head attention 对空间依赖关系进行联合建模。此外,temporal transformer被开发用于建模long-range双向时间依赖。与现有的工作相比,STTNs能够对长期的空间-时间依赖关系进行高效和可扩展的训练。
-
实验结果表明,在真实的PeMS-Bay和PeMSD7(M)数据集上,STTNs具有与当前技术水平相当的竞争力,特别是在长期交通流量预测方面。
一个节点的未来交通状况是由其邻近节点的交通状况、观测的时间步长以及交通事故、天气状况等突变决定的。在本节中,我们开发了一个ST blocks来整合空间和时间的transformer,以联合建模交通网络中的空间和时间依赖性,以精确预测 将spatial transformer S和temporal transformer T 叠加生成3D输出张量。采用剩余连接进行稳定训练。在第l ll个时空块中,spatial transformer S 和图邻接矩阵A AA中提取空间特征自注意力机制来模拟时间上的依赖性。时间Transformer的输入是一个时间序列 

2.4.3 Autoformer自相关机制
(基于随机过程理论,对离散的时间过程{tx},并对其计算自相关系数,并借助快速傅里叶变换)
论文标题:Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting
论文链接:[
提出了名为Autoformer的模型,主要包含以下创新:
-
突破将序列分解作为预处理的传统方法,提出深度分解架构(Decomposition Architecture),能够从复杂时间模式中分解出可预测性更强的组分。
-
基于随机过程理论,提出自相关机制(Auto-Correlation Mechanism),代替点向连接的注意力机制,实现序列级(series-wise)连接和O(LlogL)复杂度,打破信息利用瓶颈。
自相关机制: 基于随机过程理论,通过离散的时间过程,来计算自相关系数。不同周期的相似相位之间通常表现出相似的子过程,我们利用这种序列固有的周期性来设计自相关机制,其中,包含基于周期的依赖发现(Period-based dependencies)和时延信息聚合(Time delay aggregation)。实现高效的序列级连接,从而扩展信息效用
具体过程和主要公式:

自相关系数表示序列与它的延迟之间的相似性。我们将这种时延相似性看作未归一化的周期估计的置信度,即周期长度为T的置信度为R(T)。
时延信息聚合: 为了实现序列级连接,我们需要将相似的子序列信息进行聚合。我们这里依据估计出的周期长度,首先使用Roll()操作进行信息对齐,再进行信息聚合,我们这里依然使用query、key、value的形式,从而可以无缝替代自注意力机制

自相关系数RXX(τ)可以使用快速傅立叶变换(FFT)得到,计算过程如下:
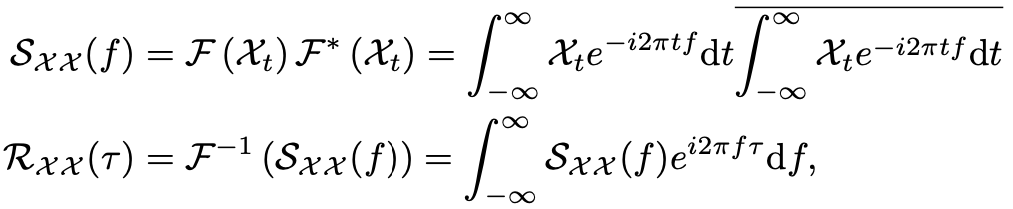
其中,F和F−1分别表示FFT和其逆变换。因此,自相关机制的复杂度为O(LlogL)。相比于之前的注意力机制或者稀疏注意力机制,自注意力机制(Auto-Correlation Mechanism)实现了序列级的高效连接,从而可以更好的进行信息聚合,打破了信息利用瓶颈。
2.4.4 FEDformer频域增强注意力
(一般信号在频域上具有稀疏性,也就是说,在频域上只需保留很少的点,就能几乎无损的还原出时域信号。保留的点越多,信息损失越少,反之亦然。虽然无法直接理论证明在频域上应用各种神经网络结构能够得到更强的表征能力。但在实验中发现,引入频域信息可以提高模型的效果,)
论文标题:FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting
论文链接:[
在Auttoformer的基础上添加了小波增强和频域变换,
FEDformer 中两个最主要的结构单元的设计灵感正是来源于此。Frequency Enchanced Block(FEB)和 Frequency Enhanced Attention(FEA)具有相同的流程:频域投影 -> 采样 -> 学习 -> 频域补全 -> 投影回时域:
整体架构:

-
首先将原始时域上的输入序列投影到频域。
-
再在频域上进行随机采样。这样做的好处在于极大地降低了输入向量的长度进而降低了计算复杂度,然而这种采样对输入的信息一定是有损的。但实验证明,这种损失对最终的精度影响不大。因为一般信号在频域上相对时域更加“稀疏”。且在高频部分的大量信息是所谓“噪音”,这些“噪音”在时间序列预测问题上往往是可以舍弃的,因为“噪音”往往代表随机产生的部分因而无法预测。相比之下,在图像领域,高频部分的“噪音”可能代表的是图片细节反而不能忽略。
-
在学习阶段,FEB采用一个全联接层 R 作为可学习的参数。而 FEA 则将来自编码器和解码器的
-
信号进行cross-attention操作,以达到将两部分信号的内在关系进行学习的目的。
-
频域补全过程与第2步频域采样相对,为了使得信号能够还原回原始的长度,需要对第2步采样未被采到的频率点补零。
-
投影回时域,因为第4步的补全操作,投影回频域的信号和之前的输入信号维度完全一致。
频域增强注意力:

传统Transformer中采用的Attention机制是平方复杂度,而 Frequency Enhanced Attention(FEA)中采用的Attention是线性复杂度,这极大提高了计算效率。因为 FEA 在频域上进行了采样操作,也就是说:“无论多长的信号输入,模型只需要在频域保留极少的点,就可以恢复大部分的信息”。采样后得到的小矩阵,是对原矩阵的低秩近似。作者对 低秩近似与信息损失的关系进行了研究,并通过理论证明,在频域随机采样的低秩近似法造成的信息损失不会超过一个明确的上界。证明过程较为复杂,有兴趣的读者请参考原文。
傅立叶基和小波基均基于傅立叶变换进行介绍,同理,小波变换也具有相似的性质,因而可以作为FEDformer的一个变种。傅立叶基具有全局性而小波基具有局部性。作者通过实验证明,小波版的FEDformer可以在更复杂的数据集上得到更优的效果。但小波版的FEDformer运行时间也会更长。
主要公式:

2.4.5 PYformer金字塔注意力
论文标题:Pyraformer:Low-complexity pyramidal attention for long-range time seriesmodeling and forecasting
论文链接:吡喃反应器:用于长程时间序列建模和预测的低复杂度金字塔关注|打开审阅 (openreview.net)
代码链接:
解决问题:
1)紧凑地捕获不同范围的时间依赖性 ,包括长期和短期预测
2)简洁的模型以及更低的计算消耗。 值得注意的是处理远程依赖中更困难的任务(可以类比长期预测),其特点是在时间序列中任意两个时间节点最长的信号遍历路径的长度,路径越短,捕捉的关键依赖就越好(注意力权重越高)
1、提出基于多分辨率表示的Pyraformer来捕捉时间序列多个范围下的时间关联,统计Pyraformer和先进方法视图,并比较了复杂度和最长信号遍历路径的长度。 2、理论上,通过合理地调整相应超参,实现O(1)的最大路径长度和O ( L )的时间与空间复杂度。 3、提出的Pyraformer在多个真实数据集上的单步时间序列预测和多步时间序列预测性能要好过原始Transformer及其变体,并且消耗的时间和内存更少。
文章对已有的tansformer模型简单的梳理:
稀疏Transformer :该部分主要是统计一下已经被提出的稀疏Transformer,比如LongTransformer、Reformer、ETC。
LongTransformer采用与CNN类似的局部窗口,将复杂度降低到O(AL),其中 A 是局部窗口大小,但有限的窗口大小使得全局交换信息变得困难。 Reformer利用局部敏感哈希 (LSH) 将序列划分为几个bucket,Reformer的最大路径长度与bucket的数量成正比,更糟糕的是,需要很大的bucket来降低复杂度 ,ETC设计的全局token数目为G,通常会随着L的增加而增加,并且随之而来的复杂度仍然是超线性的。
层次Transformer :简要回顾提高 Transformer 捕获自然语言层次结构的能力的方法,重点有两个:Multi-scale Transformer和BP-Transformer。
Multi-scale Transformer 使用自上而下和自下而上的网络结构学习序列数据的多尺度表示,可以适当地减少原始Transformer的复杂度,但还是陷入L^2的复杂度。 BP-Transformer递归地将整个输入序列划分为两个,直到最后一个分区只包含一个标记。然后,分割后的序列形成一棵二叉树,与图密切相关。Pyraformer也是形成一棵树。与 Pyraformer 相比,BP-Transformer 与更密集的图相关联,因此导致O(Llog(L))的更高复杂度。
整体架构图:

具体运行流程为:首先,将输入的历史观测值嵌入特征、全局时间协变量嵌入特征、位置编码相加在一起,与长程时间序列预测模型Informer的做法是一样的。然后,构建多分辨率的卷积模块,利用细尺度下的原始序列节点生成较粗尺度下的父节点,父节点的数目是子节点的C倍,最终形成细尺度和较粗尺度的$C$叉树,较粗尺度的节点汇聚了上一层子节点的特征信息。为了进一步地捕捉不同范围下的时间依赖,将CSCM生成的粗细度时间节点特征传入金字塔注意力模块,基于注意力机制进行节点尺度间和尺度内的信息传递。最后,针对单步预测和多步预测,采用不同的预测方法来预测结果。
金字塔注意力模块(PAM):
可以将金字塔图分解为两部分:尺度间和尺度内连接。尺度间连接将金字塔图的最细尺度与原始时间序列的每小时观测值相关联,则较粗尺度上的节点可以视为时间序列的每日、每周甚至每月特征。尺度内连接将每层尺度的邻居节点连接起来。较粗尺度相比较细尺度更适合描述长期相关性。


并将原有的attention变换为





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 如何使用 Uni-app 实现视频聊天(源码,支持安卓、iOS)
· C# 集成 DeepSeek 模型实现 AI 私有化(本地部署与 API 调用教程)