算法导论--找出所缺的整数以及VLSI芯片测试
这是《算法导论》第四章的思考题,原先准备问老师的,网上搜了一下,找到了答案。
算法导论-4-2 找出所缺的整数
【转】http://www.cnblogs.com/longdouhzt/archive/2011/07/15/2107742.html
问题: 某数组A[1..n]含有所有从0..n的所有整数,但其中有一个整数不在数组中,通过利用一个辅助数组B[0..n]来记录A中出现的整数,很容易在 O(n)时间内找出所缺的整数。但在这个问题中,我们却不能由一个单一操作来访问A中的一个完整整数,因为A中元素是以二进制表示的。我们所能用的唯一操 作就是“取A[i]的第j位”这个操作所花时间为常数。
证明:如果访问数组A中信息的唯一方式是这种单一位操作,仍能在O(n)时间内找出所缺的整数。A之外的任一完整整数仍然可以由一个单一操作来访问。【算 法导论 中文版 P50
基本方法就是用二分法:
2, 遍历数组A[1...n]的第一位, 分成两个组:Q1[1]和Q0[1],分别代表第一位是1,0的数,并记录1的个数CountA,代价为O(n)
3, 比较CountN和CountA的值,结果可能有两种情况CountN = CountA,或者CountN = CountA + 1, 前者表明所缺数的第一位为0, 后者为1,代价为O(1)
4, 通过3的结果,随后我们可以在P1[1]和Q1[1](CountN>CountA,即缺少第一位为1的数) 或者 P0[1]和Q0[1](CountN=CountA,即缺少第一位为0的数)中的第2位中重复步骤1,2中的操作,记录数组P1[2]、P0[2]和 CountN'及Q1[2]、Q0[2]和CountA'。代价为O(n/2)和O(n/2), 经过比较后可得到所缺数第二位是0还是1,决定接下来比较P1[2]和Q1[2] 或者 P0[2]和Q0[2],代价O(1)
5, 不断重复Ceiling(lg(n))次,最后即可找到所缺数总代价为2* (O(n) + O(n/2) + ... +O(n/pow(2, k))) + ... + O(1)) = 2* O(2n) = 4*O(n) = O(n)
当然这里忽略了一个问题,如果A中缺了一个,这应该是n-1个数,则多出来的那个数是什么呢,如果和其他数有重复,上面的方法就无效了,情况变得相当复杂。因此上面的只适用于多出的一个数为0,或者干脆就只有n-1个数。
【另】
比较犀利的方法:凑m,m=4k-1,并且是4k-1>=n的最大整数(比如n=7,则m=7;n=16,则m=19;n=21,m=23以此类推)
那么只需要A[1]^A[2]^……^A[n-1]^A[n]^{A[m-2]^A[m-1]^A[m]},即可
原因:从4的整数倍开始,连续4个数字异或,结果为(例如4^5^6^7的结果是0;204^205^206 = 207;8^10^11=9)
所以0^1^2^……^m的结果为0,却哪个数字,则A[1]^A[2]^……^A[n-1]^A[n]^{A[m-2]^A[m-1]^A[m]}的结果就是所缺的数字
算法导论-4-6 VLSI芯片测试
http://blog.csdn.net/wenlei_zhouwl/article/details/5960195
http://blog.csdn.net/liu1064782986/article/details/7411720
问题:Diogenes 教授有n个被认为是完全相同的VLSI芯片,原则上它们是可以互相测试的.教授的测试装置一次可测试二片,当该装置中放有两片芯片时,每一片就对另一片作测试并报告其好坏.一个好的芯片总能够正确的报告另一片的好坏,但一个坏的芯片的结果就是不可靠的.这样,每次的测试的四种可能结果如下: 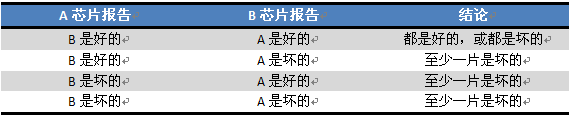
a)证明若少于 n/2 的芯片是坏的,在这种成对测试方式下,使用任何策略都不能确定哪个芯片是好的.
b)假设有多于 n/2 的芯片是好的,考虑从 n 片中找出一片好芯片的问题.证明 n/2 对测试就足以使问题的规模降至近原来的一半.
c)假设有多于 n/2 的芯片是好的,证明好的芯片可用 O(n) 对测试找出。
算法分析:
a)采用穷举法,将任何一片芯片与其它所有芯片进行比较,因为有多于n/2的芯片是坏的,且坏的芯片可以联合起来欺骗教授,则测试结果是不可靠的,无法判断出该芯片是好是坏。
b)假设:设有a个好的芯片数,b个坏的芯片数,z对测试结果为全好的测试对,其中芯片全为好的测试对为x,芯片全为坏的测试对为y,x+y=z。
二分测试思想:
1.随机的两两配对,则共有⌊n/2⌋对,分别测试。
2.根据问题描述:如果测试结果为一好一坏,或者两坏,那么把这对丢弃;如果测试结果为两好,那么随意丢弃其中一个,留下一个(若n为奇数,则剩余一个芯片没有配对。若z为奇数,丢弃这个芯片;若z为偶数(0也看做偶数),留下这个芯片)。这样操作后,留下的好芯片数一定还是大于坏的芯片数的,且经过⌊n/2⌋对测试后,原问题的规模降低了近一半。
3.重复第2步,当n<=2时,就只剩下了好的芯片。
证明:
测试结果为一好一坏或者两坏的芯片对中至少一片是坏的,把这对丢弃能保证剩下的芯片中好芯片的数量仍大于坏芯片的数量。
测试结果为全好的,这对芯片有可能全为好,有可能全为坏,随意丢弃其中一个,留下 一个。设好芯片的对数为x,坏芯片的对数为y。考虑n的情况:
若n为偶数,则x>y,所以留下的好芯片数还是大于坏的芯片数;
若n为奇数,则剩余一个没有配对的芯片。考虑z的情况:
若z是奇数,则x>y,丢弃这个芯片,这样留下的好芯片数还是大于坏的芯片数;
若z是偶数,考虑这个芯片的情况:
若芯片是好的,则x>=y,留下这个好的芯片,这样留下的好芯片数还是大于坏的芯片数;
若芯片是坏的,则x-y>=2,留下这个坏的芯片,这样留下的好芯片数还是大于坏的芯片数。
综上所述,留下的好芯片数一定还是大于坏的芯片数的。
c)采用b中的操作方法,递归式为:f(n) = f(n/2) + n/2。这个递归式符合主定理中的第三种情况,所以好的芯片可用Θ(n)对测试找出。


