蓦然回首,灯火绚烂
概率期望dp
换教室
对于每次的选择,只对当前已经下一次选择的期望有影响
并不会造成之后选择的概率不同
奖励关
\(n<=15\) ,需要联想到状压
应用状压思想,记录状态dp
概率充电器
换根dp
对于分为两次dfs,第一次记录从下到上,第二次更新从上到下
做题时可以根据打出的表及打表过程找思路,不是干看数据想做法
游走
求给边编号之后从1走到n的期望最下,编号后用高斯消元即可
给边编号时 当此条边走过的期望越大,编号越小
对于点 \(a_i\) 来说,对周围一圈每一条边的影响都为 \(a_i\) 的期望 / \(a_i\) 所连边的个数
实质上边的期望就转化为边的两边的点的期望的一部分相加
对于点的期望,和边的期望类似,也是:
$Σ_i^{所连点数}$ 周围的点的期望 / 该点所连点的个数
同样用高斯消元解决
( 此时点的期望可以理解为在这个点存在的相对次数的期望 )
最初点为1,所以 \(w_1\) 的期望要 +1
当走到n时,不会再向外走,也就不会对其他点或者相邻边作出贡献,故贡献为0,\(w_n\) =0
以上两个特殊情况在初始化第一次高斯消元的数组时特殊处理即可
斜率优化dp
特别行动队
斜率优化板子
题意:将一串数字分为若干段,每段权值 \(w=a*x_0^2+b*x_0+c\),其中\(x_0=Σ_{n=i}^jx_n\) ,求总权值和最大(a,b,c,均给出且 a<0)
由题意得朴素转移方程:\(dp_i=max(dp_j+a*(s_i-s_j)^2+b*(s_i-s_j)+c)\) (s为前缀和)
时间复杂度为 \(O(n^2)\)
对柿子进行优化
假设 \(k<j<i\) 且对于i来说,从 \(j\) 转移过来比 \(k\) 更优
得到:\(dp_j+a*(s_i-s_j)^2+b*(s_i-s_j)+c>dp_k+a*(s_i-s_k)^2+b*(s_i-s_k)+c\)
化简并将含i的柿子提到一起:\(dp_j-dp_k+a*(s_j^2-s_k^2)-b*(s_j-s_k)>2*a*s_i*(s_j-s_k)\)
\(\frac{dp_j-dp_k+a*(s_j^2-s_k^2)-b*(s_j-s_k)}{2*a*s_i*(s_j-s_k)} < s_i\) (a<0,注意变号)
将左侧的一串柿子记作 \(xl(j,k)\)
得到 \(xl(j,k)<s_i\) 时,\(j\) 比 \(k\) 更优
而且当 \(xl(i,j)<xl(j,k)\) 时,\(j\) 一定不是最优解(分情况讨论)
所以我们对于斜率只需要维护一个递增的单调队列即可(每次不断删去符合条件但较劣的点,因为\(s_i\)一定是单调递增,所以此点之后也不会更优,直接删去,取符合条件的最优的点,符合单调队列特性)
其他理解方式
对于柿子 \(dp_i=max(dp_j+a*(s_i-s_j)^2+b*(s_i-s_j)+c)\) 的右半部分在化简后可以看作三部分:
第一部分:只含有关于 \(j\) 的变量 \((dp_j+a*s_j^2-b*s_j)\) ,记作 \(A_j\)
第二部分:同时含有关于 \(i,j\) 的变量 \((-2*a*s_i*s_j)\) ,记作 \(B_j*x\)
第三部分:只含有关于 \(i\) 的变量和一切常量 \((a*s_i^2+b*s_i+c)\)
当对 \(j\) 与 \(k\) 进行比较时,第三部分忽略不计
将第二部分移到一侧,第三部分移到另一侧后再把 \(B_j\) 部分除过去
得到的柿子实质上是 \(\frac{A_j-A_k}{B_j-B_k}>x\) 或 \(\frac{A_j-A_k}{B_j-B_k}<x\)
此时柿子左侧其实就是斜率的形式
此时维护的单调队列会形成一个上(下)凸包
需要找的极值实际上就是图像和一条斜率为 \(x\) 的直线的交点(只是实际找时按照单调队列的方法找)
每次所剔除的点就是不能满足仍是凸包的点
仓库建设
板子
对于第 \(i\) 个仓库到第 \(j\) 个仓库都运到第 \(j\) 个仓库的费用:\(w=Σ_{a=i}^jp_a*x_i-Σ_{a=i}^j(p_a*x_a)\)(可以用前缀和优化)
朴素柿子为:\(dp_i=dp_j+w(i,j)\)
展开:\(dp_i=dp_j+(n_i-n_j)*x_i-(s_i-s_j)+c_i\)
设 \(k<j<i\)且对于 \(i\) 来说 \(j\) 比 \(k\)更优
得到: \(dp_j+(n_i-n_j)*x_i-(s_i-s_j)+c_i < dp_k+(n_i-n_k)*x_i-(s_i-s_k)+c_i\)
化简: \(\frac{dp_j-dp_k+s_j-s_k }{n_j-n_k} < x_i\)
当 \(xl(j,k)<x_i\) 时,\(j\) 比 \(k\) 更优
可得 \(xl(i,j)<xl(j,k)\) 的情况不成立
维护单调递增序列
关于这个题的 \(hack\) 数据:对于我们每个状态 \(dp_i\)实际上表示的是在 \(i\) 处建工厂的从 1 到 \(i\) 的最小费用,实际上最后有可能不需要建造工厂( \(p_n=0\) )我们去寻找从最后一个 \(p_i≠0\) 的位置到 \(n\) 中的最小值即可
玩具装箱
也是板子
朴素柿子为:\(dp_i=min(dp_j+(s_i-s_j+i-j-L-1)^2)\)
当 \(j\) 比 \(k\) 更优时:\(\frac{dp_j-dp_k+(s_j+j)^2-(s_k+k)^2+2*(s_j+j-s_k-k)*(L+1)}{2*(s_j+j-s_k-k)} < s_i+i\)
维护一个单调递增序列
土地购买
主要问题在于如何推出朴素的柿子
对于第 \(i\) 块土地,如果它被第 \(j\) 块完全覆盖掉,那么第 \(i\) 块土地就不会对答案产生影响
我们首先将所有会对答案产生影响的土地筛出来:
将所有土地以长为第一关键字,宽为第二关键字进行从小到大的排序
此时,我们得到了一个关于长单调不递增的数对
可知只要存在 \(w_i<w_j\) 且 \(i<j\) ,那么 \(i\) 就会被覆盖
筛完之后,我们也就是得到了一个长单调递减,宽单调递增的序列
所以对于任意 \(i,j (i>j)\) ,合并后的从第 \(i\) 块到第 \(j\) 块土地的价格为 \(l_j*w_i\) (这一区间里 \(l_{max}=l_j,w_{max}=w_i\) )
易得转移方程:\(dp_i=min(dp_j+l_{j+1}*w_i)\)
进行优化:当 \(\frac{dp_j-dp_k}{l_{k+1}-l_{j+1}} < w_i\) 时,\(j\) 比 \(k\) 更优
维护一个单调递增序列
卡特兰数
网格
卡特兰数的两种理解方式
第一种:
对于一个由n个+1和n个-1组成的数列,有多少种排序方式能使得所有前缀和均为非负数?
对于任何一个不成立的情况,最先开始不成立的位置是有k+1个-1和k个+1
将这2k+1个数全部取反
此时可得到一个n+1个+1,n-1个-1的序列,这种序列和所有不合法序列是一一对应的
而这样的序列的数量为 \(\binom{2n}{n+1}\)
所有序列的数量为 \(\binom{2n}{n}\)
合法序列的数量(卡特兰数) \(C_n=\binom{2n}{n}-\binom{2n}{n+1}=\frac{\binom{2n}{n}}{n+1}\)
递推柿子 \(C_n=\frac{4n-2}{n+1}C_{n-1}\)
递归柿子:\(C_n=\sum_{i=0}^{n-1}(C_i \times C_{n-i-1})\)
第二种:
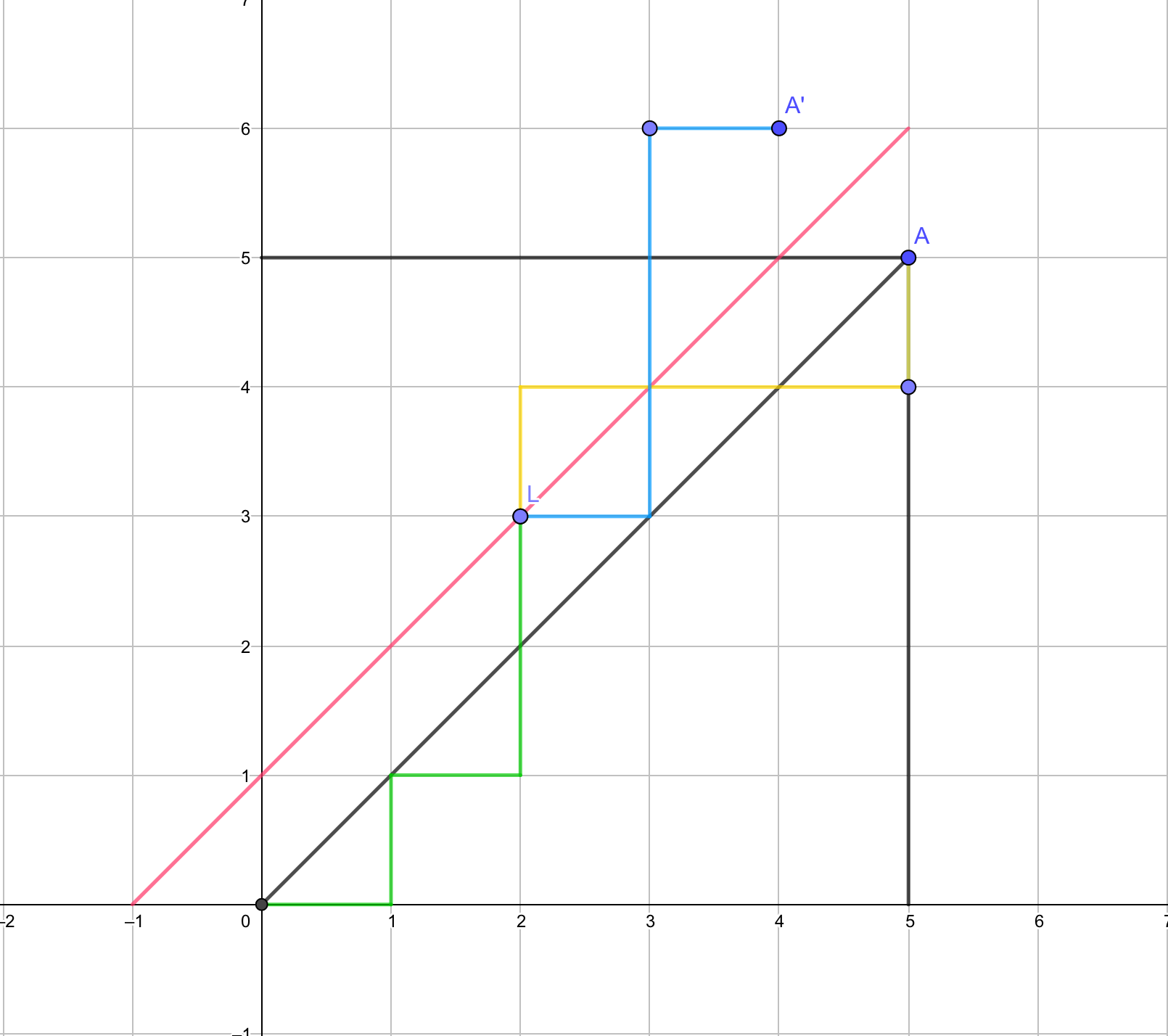
对于一个 \(n \times n\) 的方格中,从 \((0,0)\) 走到 \((n,n)\) ,有多少种保证全程 \(x>=y\) 的路径?
我们已知:只要碰到 \(y=x+1\) 这条直线,就不满足要求,且所有不满足条件的路径都与直线至少有一个交点
而对从这个交点到 \((n,n)\) 的路径沿直线 \(y=x+1\) 翻折,得到一条过 \((n-1,n+1)\) 的路径
且所有到 \((n-1,n+1)\) 的路径与原路径中不合法路径一一对应
得到不合法序列数量 \(\binom{2n}{n+1}\)
合法序列的数量 (卡特兰数) \(C_n=\binom{2n}{n}-\binom{2n}{n+1}=\frac{\binom{2n}{n}}{n+1}\)
卡特兰数应用:在任意时刻一个元素的数量总是大于等于另一个元素的数量
n对括号的合法配对方案数
n+1个叶子(n个非叶节点)的满二叉树的形态数, 走到左儿子+1,走到 右儿子-1(大致同上)
n个节点的二叉树的形态数
n个数入栈后出栈的排列总数
对凸n+2边形进行不同的三角形分割的方案数(分割线断点仅为顶点,且分割线仅在顶点上相交)
n层的阶梯切割为n个矩形的切法数
再回头来看这个题,本质上就是n个+1和m个-1进行如上的变形
所有序列的数量为 \(\binom{n+m}{n}\)
合法序列的数量 \(\binom{n+m}{n}-\binom{n+m}{n-1}\)
进行化简: \(\frac{(n+m)! \times (n-m+1)}{(n+1)! \times m!}\)
如果直接用高精度会超时,分解质因数约分+高精乘
有趣的数列
实际上也是卡特兰数
这2n个数可以根据所在位数的奇偶性看作两组,且每一组内递增
所以对于一个固定的选法,它的排列顺序也是一定的
我们只需要保证每一组里的大小关系成立即可
也就是对于两组选数,第二组的每个数字都比第一组的同一位置大
实质上就是每个前缀和内 第一组的数量>=第二组的数量
符合了卡特兰数的性质
和上一题差不多,用分解质因数优化,连高精都不用了
树屋阶梯
打表打出卡特兰数,完
将一个高为n的阶梯分成n个矩形的方案数
我们已知,每一行最右侧的位置一定不属于同一个矩形,所以最右侧的位置与矩形一一对应
包含左下角的位置的矩形也是其中一个
当确定了左下角属于哪个矩形时,整个阶梯就被分成了三部分
设高为i时的方案数为 \(C_i\)

如图,当选择第三行的矩形时,整个图划分成了所选区域,高为2的阶梯和高为3的阶梯三部分, \(C=C_2+C_3\)
由此得出卡特兰数公式:\(C_i=\sum_{i=0}^{n-1}C_i+C_{n-i-1}\)
purfer序列
树的计数
根据purfer序列与无根树一一对应的性质
序列的个数就是所要求的树的个数
每个数字在序列中出现的次数 \(a_i=d_i-1\)
总出现次数 \(\sum_{i=1}^{n}a_i=n-2\)
序列的个数就看作一个重排列计算 \(ans=\frac{(n-2)!}{\prod_{i=1}^{n}(d_i-1)!}\)
记得先去判断不成立的情况 (度数为0且节点数大于1、出现次数和不等于n-2……)
明明的烦恼
调了大半天结果柿子没问题,代码出锅了
所有数据分为两部分
第一部分是给出度数的,设\(sum=\sum_{i=1}^{n}(d_i-1)\)它们的全排列数是: \(\frac{sum!}{\prod_{i=1}^{n}(d_i-1)!}(d_i\neq-1)\)
另一部分是没有给出度数的,设 \(num=\sum_{i=1}^{n}(d_i=-1)\)
由 \(序列长度=n-2\) 得 对于 \(n-2-sum\) 个序列中的位置来说,每个位置都有 \(num\) 种可能性,这些点的全排列数是:\(num^{n-2-sum}\)
当这两部分各种按顺序合并时,相当于在将其中一个排列分成 (另一个排列的长度+1) 个可空子串,方案数为:\(\frac{(n-2)!}{sum!(n-sum-2)!}\)
以上几个柿子合并
\(ans=\frac{(n-2)!}{\prod_{i=1}^{n}(d_i-1)! \times (n-sum-2)!} \times num^{n-2-sum}\)
BSGS
Discrete Logging
bsgs板子
bsgs用来解决 \(x^y \equiv z \mod q\) 中已知 \(x,z\) 和 \(q\) 时求最小非负 \(y\) 的值的问题
步骤:
-
设 \(y=a*m-b\) ,其中 \(m=\left \lceil \sqrt{z} \right \rceil\),且 \(a\in [0,m],b\in[1,m]\)
-
此时原式可表示为:\(x^{a*m}\equiv z\times x^b \mod q\)
-
将所有 \(z\times x^b\) 的值处理出来,用哈希表(或者map)存下来
-
再枚举 \(x^{a\times m}\) 的值,如果有相等的值, \(ans=a*m-b\)
证明如图(不是很会证)

计算器
三个板子
\(work1:快速幂\)
\(work2:同余方程\)
\(work3:BSGS\)
随机数生成器
先推柿子
\(x_i=(a*x_{i-1}+b )\% p\)
\(x_2=(a*x_1+b )\%p\)
\(x_3=(a^2*x_1+a*b+b )\%p\)
\(x_n=(a^{n-1}*x_1+\sum_{i=0}^{n-2}(a^i*b) )\%p\)
\(x_n=(a^{n-1}*x_1+b* \sum_{i=0}^{n-2}a^i )\%p\)
设 \(S=\sum_{i=0}^{n-2}a^i\)
得到 \(a*S=\sum_{i=1}^{n-1}a^i\)
上下相减 \((a-1)*S=a^{n-1}-1\)
得到 \(S=\frac{a^{n-1}-1}{a-1}\)
代回原柿子 \(x_n=(a^{n-1}*x_1+b* \frac{a^{n-1}-1}{a-1})\%p\)
即 \(t=(a^{n-1}*x_1+b* \frac{a^{n-1}-1}{a-1})\%p\)
化简移项 \(a^{n-1}=\frac{(a-1)*t+b}{(a-1)*x+b} (\mod p)\)
变成了裸的 \(bsgs\),结果求的是 \(n-1\),记得加一
然后就痛苦起来了
细节:当\(a=0\) 和 \(a=1\)时,柿子没意义,需要特判
\(a=0\) 时判断 \(t\) 与 \(b\) 是否相等
\(a=1\) 时柿子变为了 \(b*(n-1)\equiv t-x (\mod p)\)
上面的那个柿子求逆元时,因为 \(p\) 为质数,可以用费马小定理求逆元,但记得先 \(\%p\) 一下再算
Matrix
矩阵上套一个板子
平衡树
营业额统计
找最小差值 $\rightarrow $ 平衡树板子
宠物收养所
也是找最小差值,多了个删除 $\rightarrow $ 平衡树板子
郁闷的出纳员
设定一个数字表示截止目前总的工资的变化量
每次裁员/入职时先对数字操作一下再进行
也可以正常写树上的 \(lazy\) 标记(当作区间运算来做)
由于数据过水,甚至每次增加工资时直接将整棵树跑一边也行...
火星人prefix
求树的哈希值: \(hash_{rt}=hash_{lson}*base^{num_{rson}+1}+s_{rt}*base^{num_{rson}}+hash_{rson}\)
(同普通 \(hash\) 求法)
用平衡树维护这些树的哈希值
查询时对长度进行二分判断哈希值是否相等
最长上升子序列
维护一条动态序列的信息:平衡树
由于新插入的数字不会对之前的答案造成影响(求上升序列,插入的数字递增),我们可以直接用线段树将最后的序列处理出来
再对这条序列求最长上升子序列,处理出答案
星系探索
给定一棵树,进行如下操作:
1.求节点x到根节点的权值和
2.将x节点的父亲换为y节点
3.将以x为根的子树中所有节点的权值加上常数k
绝大部分情况下,我们都将在树上的操作通过 \(dfs\) 序转化为对序列操作,此题亦然(用的是欧拉序)
入栈的权值为正,出栈的权值为负
两节点的路径和就转化为了区间和(两节点要求有父子关系,此题为到根节点的路径和,满足条件)
增加权值也就转化成了区间加法,打懒标记
换根操作可以将x所在的整个区间移到 \(y\) 区间内(要求贴着 \(y\) 区间的其中一侧以保证不混入其他子树),即为区间平移
实现的时候我的做法应该是比较麻烦的
先记录一下每个节点入栈和出栈所对应的 \(x\)( \(x\) 和所对应的节点全程是不会改变的)
保证查询区间时不越界,在左右两侧各插入一个数字
在 \(build\) 时记录一下每一个 \(x\) 对应的是节点的出栈还是入栈
如果是出栈,权值改变时做减法
还要额外记录以 \(x\) 为节点的子树中出栈和入栈的个数(计算 \(sum\) 时使用)
其他就正常(?)写平衡树就行
分块&莫队
弹飞绵羊
对于单个块内维护弹出该块所需次数和弹出后所在位置
每次询问时,在 $ \sqrt n $ 个块上跳跃,暴力即可
蒲公英
题意:求区间内众数
预处理出每个区间内颜色的前缀和
每次询问时通过前缀和 \((n)\) 和暴力加上零散位置 \((\sqrt n)\) 求出众数
复杂度 \(O(m*(n+\sqrt n))\) , 理论过不去,实际 \(O(能过)\)
正确复杂度做法:
多预处理出来一个任意一段区间内的众数的数组
(枚举左右端点,暴力修改查询),复杂度
\((O( \sqrt n \sqrt n \sqrt n))=O(n\sqrt n)\)
每次查询时复杂度也是 \(O(\sqrt n)\)
总复杂度 \(O(m\sqrt n+n\sqrt n)\) 能过了
教主的魔法
分块经典板子
对于每个区间内进行排序
查询时整块内二分查找
散块暴力比较
复杂度 \(O(log(\sqrt n)\sqrt n+\sqrt n)\),近似于 \(O(\sqrt n)\)
修改时类似懒标记
对于整块的修改,直接对懒标记进行操作
对于散块直接修改,顺便下放标记,重新块内排序
复杂度视作 \(O(\sqrt n)\)
总体复杂度 \(O(m\sqrt n)\)
数颜色
莫队板子
对于所有询问,对于左端点所在块为第一关键字,右端点所在块为第二关键字,时间戳为第三关键字排序
跑莫队
作业
题意:求区间内数值在 \(l\) ~ \(r\) 中数的个数与数值种类的个数
莫队套分块
用莫队对询问区间进行排序
查询统计时用分块查询 \(l\) ~ \(r\) 的区间
小b的询问
题意:求区间内所有颜色出现次数的平方和(离线)
莫队
预处理出平方差
操作时维护每个数字出现的次数与 $ ans $
颜色
上一题的在线版本
分块
预处理出:
任意一段区间内 前 \(k\) 的颜色的权值前缀和 ( \(qzh[i][j][k]\) )
所有颜色个数的前缀和 ( \(mem[i][k]\) )
(以上两个的单位都是整块)
查询时再对零散块进行操作(记录该数字出现的次数对答案进行修改)
代码实现和卡常的过程挺痛苦的
小z的袜子
预处理出每个数字对应的贡献差
维护出现次数与 \(ans\)
主席树
可持久化线段树
可以查询操作过程中任何一个状态
实现方法是每次修改时不在原来点上修改,而是复制出一个相同的点再进行修改
其余的点与之前状态共用即可
时间复杂度 \(O(logn)\) ,空间复杂度 \(O(logn)\)
唯一缺点就是空间需求量非常非常大
主席树,或者说,可持久化权值线段树
可持久化方法与普通线段树相同,不再赘述
花神的嘲讽计划
hash+分块跑过去的
你说这是主席树题单?
能跑就行(
用主席树也差不多,也是在主席树上判断一下区间是否存在这个串的hash值
K小数
主席树板子题:求区间第K大
对于每一个插入的节点建一棵主席树
求 \(l\) 到 \(r\) 的第 \(K\) 大时,在 \(l-1\) 与 \(r\) 两棵树上同时查找,寻找每一段上数量之差即可
int find(int lr,int rr,int l,int r,int k) {
if(l==r) return l;
if(num[ls[rr]]-num[ls[lr]]>=k) return find(ls[lr],ls[rr],l,mid,k);
else return find(rs[lr],rs[rr],mid+1,r,k-(num[ls[rr]]-num[ls[lr]]));
}
疯狂的颜色序列
强制在线版 HH的项链 :寻找区间内种类总数
蛮神奇的方法
在一段序列中 ,第一次出现的颜色 \(k\) 与第二次出现的 \(k\) 作出的贡献共为1,统计哪一个都没有区别
故只需要统计区间中第一次出现的颜色的个数
对于每一种颜色,用数组 \(mem_x\) 记录上一个颜色为 \(x\) 的下标
比如序列:1 2 3 2 3 5
就变成了这样:0 0 0 2 3 0
在查询区间 \(3\) ~ \(6\) 时,实际上只是查询区间内 \(mem_i\) 在 \(0\) ~ \(2\) 中的个数
而这个值的查询可以用主席树实现
森林
树上主席树+树上差分
求树上两点之间路径上的第 \(K\) 大
对于树上的每一个节点也可以建从该节点到根节点的主席树
用倍增求出 \(lca\) 后,路径上的一段权值内数字的个数为(树上差分思想):
\(num_l+num_r-num_{lca}-num_{gfa}\)
其他类似区间第 \(K\) 大
影魔
没有打懒标记却一直以为代码或者思路有问题 awa
题面挺绕的
说人话:对于范围内的任意区间 \(l\)~\(r\) 满足 \(l+1<=r-1\) ,设区间内除端点外最大值为 \(x\) ,有以下情况会对总体造成贡献:
- 当 \(x<=min(w_l,w_r)\) 时,造成 \(p1\) 的贡献
- 当 \(min(w_l,w_r)<x<max(w_l,w_r)\) 时,造成 \(p2\) 的贡献
对于范围内所有区间 \(l\)~\(r\) ,都会造成第三类贡献:
- 造成 \(p1\) 的贡献
求 \(tl\)~\(tr\) 之间的所有区间作出的贡献和
对于第三类贡献,可以直接求得:\((tr-tl)*p1\)
而前两类贡献,都是和区间最大值有关,预处理出每个点 \(x\) 为区间最大值时对应的区间范围 \(l_x\) 与 \(r_x\) (单调栈)
后面咕了
dC Loves Number Theory
求序列中任意一段区间乘积的欧拉函数,强制在线
欧拉函数通项:$φ(n)=n*\prod (1-\frac{1}{p_i}) $ ,\(p_i\) 为 \(n\) 的所有质因数
或者说这个柿子是这样的: \(n* \frac{\prod (p_i-1)}{\prod p_i}\)
\(n\) 可以靠前缀和 \(O(1)\) 求
右侧这个柿子主要就是求区间积的所有质因数
就可以看作区间内所有数字的质因数的集合,就转化成了在线版HH的项链问题
只是统计的不是数量,而是区间内点的 $ (num[i]-1)*inv(num[i]) $ 的乘积
middle
给出一个序列,求给定左端点与右端点范围的所有区间中最大的中位数,强制在线,保证范围内所有左右端点 \(l<r\)
一个求区间中位数的思路:
对于任意一个点 \(x\) ,将区间内所有大于等于 \(x\) 的数字赋为 \(1\),反之赋为 \(-1\)
当区间和 \(>=0\) 时,中位数是 \(>=x\) (此题中偶数长度序列中位数取后面那个),反之中位数 \(<x\)
再对答案二分查找即可
所有点的赋值序列可以预处理出来,对于离散化排序后的点,相邻的两个点之间只会有一个数字赋值情况不同,故可以用主席树预处理
固定区间内求中位数已经OK,回头考虑给定左右端点区间求中位数最大值
设左端点区间为 \(a\)~\(b\) ,右端点区间为 \(c\)~\(d\)
已知 \(b+1\)~\(c-1\) 的区间是必选的
因为只考虑区间和,把左右区间看作分别选一个后缀与一个前缀即可
对于任意一个 \(x\) ,如果满足 \(x\) 是给定范围内某一段区间的中位数,需保证最大区间和 \(>=0\) ,而最大区间和实际上就是中间那一段数字的和+左端点范围最大后缀和+右端点范围最大前缀和,这个值是可以直接在线段树上维护的
即使区间内中位数不是 \(x\),区间中位数也会大于 \(x\),同样满足要求,对答案进行二分
神秘数
给定一个序列,对任意区间求区间中的数字无法相加得到的正整数的最小值
根据样例胡出一些规律:
对于任意一个满足可以组成 \(1\) ~ $sum (sum=\sum _i^{i\in s}) $ 中所有数字的集合 \(s\) 来说:
若在 \(s\) 中插入一个数字 \(a\)
- 当 \(a<=sum\) 时,\(s\) 能够组成 \(1\) ~ \(sum+a\) 中的所有数字,所组成最大数字为 \(sum+a\)
- 当 \(a>sum\) 时,\(s\) 仍然能够组成 \(1\) ~ \(sum\) 中的所有数字,所组成最大数字为 \(sum\)
可以这么理解:
对于集合中从小到大排列后的数字来说,如果 \(某个数字>前缀和+1\) ,那么新的集合就不满足要求,答案就是此时的 \(前缀和+1\);反之,该数字纳入集合
根据主席树,我们能够方便的求出一段区间内值小于 \(x\) 的所有数字之和 \(w\),区间内所有值 \(<=w+1 \) 的数字可以组成新的集合
初始 \(w=0\),该集合不断延伸,直到新的 \(w=x\) ,可知该集合之外的所有数字都 \(>w+1\) ,不能组成一个更大的集合,\(w+1\) 即为所求神秘数
动态排名系统
查询动态区间第K大
需要用到树状数组套主席树(实际上这玩意应该叫树状数组套权值线段树)
对于主席树我们无法进行修改(一个点如果修改需要将之后所有的树都修改)
于是就拿树状数组去优化
在树状数组的所有节点上建权值线段树
每次修改时修改路径上所有点,复杂度 \(O(log^2n)\)
查询区间第K大时,预处理出包含前 \(r\) 个节点和前 \(l-1\) 个节点的所有权值线段树根节点
查询时一起往下跳,复杂度 \(O(log^2n)\)
int l=read(),r=read();
tr[pd].clear();tl[pd].clear();
for(int i=r;i;i-=lowbit(i))
tr[pd].push_back(root[i]);
for(int i=l-1;i;i-=lowbit(i))
tl[pd].push_back(root[i]);
int query(int l,int r,int k)
{
if(l==r) return l;
int tot=0;
for(int i:tr[pd])
tot+=size[ls[i]];
for(int i:tl[pd])
tot-=size[ls[i]];
if(k<=tot) {
tl[!pd].clear();tr[!pd].clear();
for(int i:tr[pd])
tr[!pd].push_back(ls[i]);
for(int i:tl[pd])
tl[!pd].push_back(ls[i]);
pd=!pd;
return query(l,mid,k);
}
else {
tl[!pd].clear();tr[!pd].clear();
for(int i:tr[pd])
tr[!pd].push_back(rs[i]);
for(int i:tl[pd])
tl[!pd].push_back(rs[i]);
pd=!pd;
return query(mid+1,r,k-tot);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号