【数理统计】概率统计
一、古典概型与几何概型
1.1古典概型与几何概型特征
1)共同点:等可能性(每个事件发生的概率相同)
2)区别:
- 古典概型的样本空间是一个有限集。
- 几何概型可以是无限集,但它可以用几何区域来表示
1.2公式
1)古典概型:
已知基本事件个数n与事件A所包含的结果数m,然后代入公式:
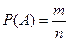
即为事件A的概率。
2)几何概型:使用有度量(长度、面积、体积等)的几何区域表示:

1.3求解步骤
1.3.1古典概型
1)判断事件是否为等可能性事件,并用字母表示所求事件;
2)利用列举法等方法计算基本事件的个数n及事件A中包含的基本事件的个数m;
3)计算事件中A的概率![]()
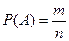
1.3.2几何概型
1)把样本空间和所求概率的事件用关系式表示出来,其中又分两类:
a、样本空间具有明显的几何意义,样本点所在的几何区域题目中已给出
b、样本空间所求事件所对应的几何区域没有直接给出,找出它们成为解这类几何概率题的关键。方法是先引进变量,然后用代数公式表示变量间的关系,再绘图根据几何形状求解。
2)在坐标系中把几何图形画出来
3)根据图像按照古典概型公式求解
例:

二、条件概率与贝叶斯
2.1定义
2.1.1条件概率

2.1.2乘法公式
由此可得到:
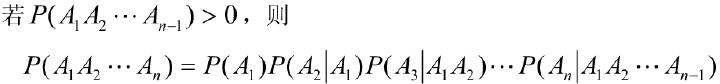
例:

注:当A属于B的时候,P(A)=P(AB)
2.1.3全概率公式:
1)原理:乘法公式的扩展
设是两个事件,那么可以表示为

显然,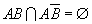 ,如果
,如果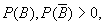 则
则
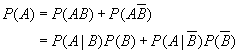
由此可得:
2)定义:
设试验E的样本空间,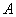 为
为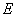 的事件,
的事件, 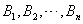 为
为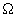 的一个分割,且
的一个分割,且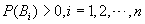 ,则
,则

上式被称为全概率公式。
例:

答


![]()
2.1.4贝叶斯公式
设试验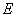 的样本空间,
的样本空间,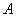 为
为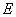 的事件,
的事件, 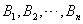 为
为 的一个分割,且
的一个分割,且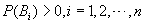 ,则
,则
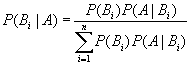
上式称为贝叶斯公式。
证明:
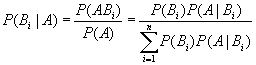
2.1.5独立事件
1)两个事件的独立
注:此时P(A|B)=P(A)=P(AB)/ P(B)
2)多个事件的独立

3)n重伯努利试验(n重独立重复试验)
二项式定理:
对于伯努利概型,事件A在n次试验中发生k次的概率为
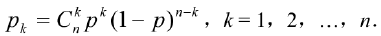
2.2条件概率中的P(B|A)特征(全概率公式和贝叶斯公式)
共同点:都是由条件概率和乘法公式推广得到的
区别:
- 全概率公式求解的是P(B),其中A被分解为A=A1+A2+...An的集合,由此分解P(B)=P(A1B)+P(A2B)+...P(AnB)来求解。
- 贝叶斯公式求解的是P(Bi|A),其被称为后验概率,P(A)被称为先验概率。可以这样理解为:导致P(A)发生的因素有很多种,B=B1+B2+...+Bn,其中由Bi导致A发生的概率就是后验概率。它可以用来分析各种前提因素的重要性。
三、大数定律与中心极限定理
3.1大数定理
多个随机变量的算数平均μ渐近
3.2中心极限定理
当n充分大时,独立同分布的随机变量X1,X2,...,Xn,且E(Xi)=μ,D(Xi)=σ2>0,则这些随机变量的和服从正态分布:

这些随机变量和的均值服从正态分布:
而![]()

四、参数估计与假设检验
 、
、4.1参数估计
4.1.1点估计
1)矩估计
2)最大似然数估计
4.1.2估计的评价标准
1)无偏性
2)有效性
3)相合性
4.1.2区间估计
置信水平(置信度):1-α
4.2假设检验
显著水平:α,取0.05,0.01和0.1
4.3参数估计和假设检验的异同
4.3.1共同点
原理都是由下式正态分布规律得到的:
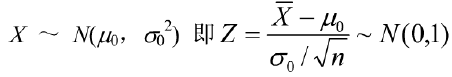

4.3.2区别
- 参数估计认为均值X(ba)落入在横坐标轴区间(-zα/2,zα/2)的概率是1-α
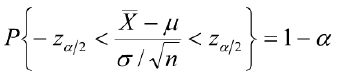
由此得到估计区间:
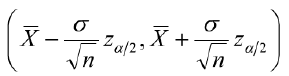
- 假设检验认为X(ba)落入在横坐标轴区间(0,-zα/2)和(zα/2,0)的事件属于小概率事件,对于给定的小概率α(0<α<1)有:
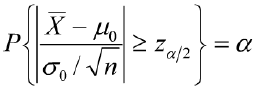
若![]() (拒绝域)成立,则拒绝原假设H0,接收H1,否则没有充分的理由拒绝H0,应该认可H0。
(拒绝域)成立,则拒绝原假设H0,接收H1,否则没有充分的理由拒绝H0,应该认可H0。
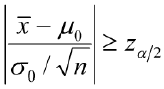 (拒绝域)成立,则拒绝原假设H0,接收H1,否则没有充分的理由拒绝H0,应该认可H0。
(拒绝域)成立,则拒绝原假设H0,接收H1,否则没有充分的理由拒绝H0,应该认可H0。4.3.3求解步骤
- 参数估计:
1、选定一个轴枢量:分布已知的z(x1,x2,...,θ)
2、确定置信区间:P{-zα/2<z(x1,x2,...,θ)<zα/2}=1-α
3、化简得到:P{θ1(x1,x2,...,xn)<θ<θ1(x1,x2,...,xn)}=1-α,则得到参数的区间估计(θ1,θ2)
- 假设检验:
1、提出原假设H0,以及备选(被择)假设H1。(其中H0和H1是对立的)
2、设原假设成立,并以此构造一个小概率的事件,其概率值为P=α
3、代入样本数据判断小概率事件是否发生,若发生则拒绝H0,认可H1。
附:排列组合公式
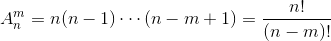
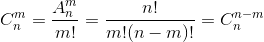
公式描述:公式中A(n,m)为排列数公式,C(n,m)为组合数公式。
参考资料:
1、刘安平,肖海军等,《概率论与数理统计》,科学出版社
2、郑州轻工业学院概率论与数理统计讲义:http://lxy.cumtb.edu.cn/gailvtongjidaoxue/gailvlunyushulitongjizhidao.htm



 浙公网安备 33010602011771号
浙公网安备 33010602011771号