查找排序算法汇总

摘要：

插入排序分为三种：

  • 直接插入排序

    基本思想就是挨个遍历，第二个元素和第一个比，第三个元素和前两个比，第四个和前三个比，如果合适就移动后面的元素，插入当前元素

  • 二分插入排序

    基于二分查找算法的思想，不挨个比，每次找中间数进行比较，如果合适就移动后面的元素，插入当前元素

  • 希尔排序

    希尔排序适用大规模且无序的数据，上述两种适合小规模且有序的数据。

    希尔排序的核心思想是分组，根据增量序列分组排序，避免大规模的数据遍历比较。

交换排序分为两种：

  • 冒泡排序

    比较相邻的元素，如果第一个比第二个大，元素交换

  • 快速排序

    递归思想：取一个基准数进行左右分区，将数组中大于基准数的放在右边，小于基准数的放在左边。

    对于左右分区，采取相同的策略，选取基准数，分区，直到单个分区中只有一个数。

选择排序分为两种：

  • 直接选择排序

    选出数组中最小的元素，放在序列起始位置，然后在剩余元素中选取最小的数据，以此类推。

  • 堆排序

    堆排序核心思想是利用数组的索引映射称为堆的数据结构（近似二叉树）。

一，查找算法

常见查找算法分为七种：

  • 顺序查找

  • 二分查找

  • 插值查找

  • 查找树

  • 分块查找

  • 哈希查找

顺序查找

顺序查找适合于存储结构为顺序存储或链接存储的线性表。

从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。【挨个遍历】

时间复杂度和空间复杂度都为O(n)。

 /**
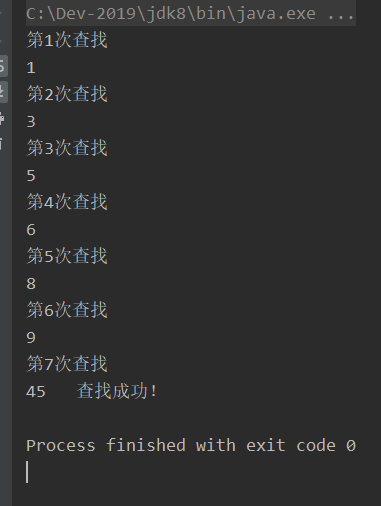
         * 顺序查找  45
         */
        int x[]=new int[]{1,3,5,6,8,9,45,56,78,86,95};

        for (int i =0 ;i<x.length;i++)
        {
            System.out.println("第"+(i+1)+"次查找");
            if(x[i]==45)
            {
                System.out.println(x[i]+"   查找成功！");
                break;
            }
            System.out.println(x[i]);
        }

1570609123946


二分查找

前提：元素必须是有序的。

基本思想：用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。

时间复杂度为O(log2n)

/**
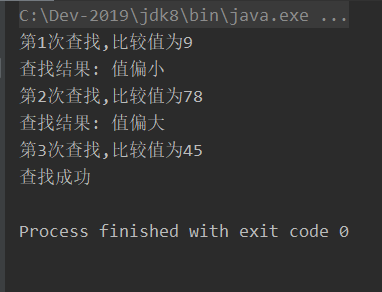
         * 二分查找  45
         */
        int x[]=new int[]{1,3,5,6,8,9,45,56,78,86,95};

        int low = 0;
        int high = x.length;
        int mid;
        int count=1;

        while(low<high)
        {

            mid=(int)(low+high)/2;

            System.out.println("第"+count+"次查找"+",比较值为"+x[mid]);

            if(x[mid]<45)
            {
                low=mid+1;
                System.out.println("查找结果: 值偏小");
            }
            else if(x[mid]>45)
            {
                high=mid-1;
                System.out.println("查找结果: 值偏大");
            }
            else
            {
                System.out.println("查找成功");
                break;
            }
            count++;
        }

1570610521790


插值查找

二分查找的优化版本，将查找点从固定的二分改为自适应，提高查找效率。

mid = low + (key - a[low]) / (a[high] - a[low]) * (high - low)

时间复杂度为O(log2(log2n))

package com.company;

public class Al
{
    public static void main(String[] args){
        /**
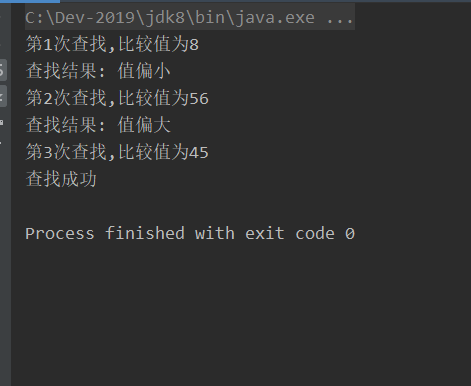
         * 插值查找  45
         */
        int x[]=new int[]{1,3,5,6,8,9,45,56,78,86,95};

        int low = 0;
        int high = x.length-1;
        int count=1;

        while(low<high)
        {

            int mid = (low + (high-low)*(45-x[low]) / (x[high] - x[low]));

            System.out.println("第"+count+"次查找"+",比较值为"+x[mid]);

            if(x[mid]<45)
            {
                low=mid+1;
                System.out.println("查找结果: 值偏小");
            }
            else if(x[mid]>45)
            {
                high=mid-1;
                System.out.println("查找结果: 值偏大");
            }
            else
            {
                System.out.println("查找成功");
                break;
            }
            count++;
        }
    }
}

1570611336971


查找树

二叉查找树

  • 二叉查找树定义：

每棵子树头节点的值都比各自左子树上所有节点值要大，也都比各自右子树上所有节点值要小

二叉查找树的中序遍历序列一定是从小到大排列的。

  • 查找思路：

假设查找值为x，b为二叉查找树

若b是空树，则搜索失败，否则：
若x等于b的根节点的数据域之值，则查找成功；否则：
若x小于b的根节点的数据域之值，则搜索左子树；否则：
若x大于b的根节点的数据域之值，则搜索右子树。

平衡二叉树

红黑树

B树

B+树


分块查找（索引）

分块查找又称索引顺序查找，它是顺序查找的一种改进方法。

算法思想：将n个数据元素”按块有序”划分为m块（m ≤ n）。每一块中的结点不必有序，但块与块之间必须”按块有序”；即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……
算法流程：
　　step1 先选取各块中的最大关键字构成一个索引表；
　　step2 查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；然后，在已确定的块中用顺序法进行查找。


哈希查找

哈希查找的操作步骤：

  1.   用给定的哈希函数构造哈希表；

  2.   根据选择的冲突处理方法解决地址冲突；

  3.   在哈希表的基础上执行哈希查找。

二，排序算法

关于排序算法

相关概念：

正序：关键码从小到大排列

逆序：关键码从大到小排列

稳定性：对于相同元素，排序后次序保持不变称为稳定，若次序发生变化称为不稳定。


排序算法选用的数据结构：

线性表两种典型的存储结构为顺序表和链表，顺序表具有随机存取的特性，存取任意一个元素的时间复杂度为O(1)，

链表存储任意一个元素的时间复杂度为O(n)。所以排序算法大多基于顺序表构建。


排序算法性能评估：

  • 时间复杂度（由于使用次数频繁，需要着重考虑）
  • 空间复杂度（排序算法使用空间通常都不大，不作为主要矛盾）
  • 算法复杂度

排序算法宏观分类

排序算法可以分为内部排序和外部排序，内部排序适用元素不多的文件，可以全部放在内存中执行排序。对于较大文件，由于内存容量的限制，通常使用外部排序。（外部排序比内部排序慢的多）


内部排序分类：

比较排序

  • 直接插入排序
  • 二分插入排序
  • 希尔排序
  • 冒泡排序
  • 快速排序
  • 直接选择排序
  • 堆排序
  • 归并排序

快速排序，堆排序，归并排序时间复杂度都为O（nlog2n）

希尔排序的时间复杂度与增量序列有关，目前最小能达到O(n1.5)

直接插入排序，冒泡排序，直接选择排序时间复杂度为O（n2）

非比较排序

  • 计数排序
  • 桶排序
  • 基数排序

时间复杂度为O（n）

插入排序

插入排序基本思想：将待排序的元素按照关键码的大小插入到已经排好序的一组记录的适当位置上。

直接插入排序（顺序查找算法）

对已经排好序的序列挨个遍历，比较大小，然后移动元素，插入。

PS：从第二个元素开始，先跟第一个元素比。然后第三个元素和1,2,比，第4个元素和前三个比。

如果需要逆序输出：x[j] > temp改为x[j] < temp

/**
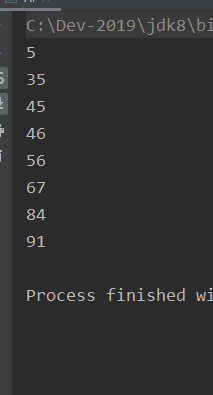
         * 直接插入排序
         */
        int x[] = new int[]{45,56,84,5,67,91,35,46};

        for(int i = 1;i < x.length;i++)
        {
            int temp = x[i];    //从第二个元素开始遍历

            int j = 0;

            for(j = i - 1;j >= 0 && x[j] > temp;j--)   //如果第一个元素大于第二个元素
            {
                x[j + 1] = x[j];   //第一个元素后移
            }
            x[j + 1] = temp;       //将元素插入第一个元素前

            //以此类推

        }
        for (int i = 0; i < x.length; i++)
        {
            System.out.println(x[i]);
        }
    }

1570612773035

二分插入排序（二分查找算法）

/**
         * 二分插入排序
         */
        int x[] = new int[]{45, 56, 84, 5, 67, 91, 35, 46};

        for (int i = 1; i < x.length; i++) {
            int temp = x[i];
            int low = 0;
            int high = i - 1;
            int mid;
            while (low <= high) {
                mid = low + (high - low) / 2;
                if (x[mid] > temp) {
                    high = mid - 1;
                } else {
                    low = mid + 1;
                }
            }
            for (int j = i - 1; j >= low; j--) {
                x[j + 1] = x[j];
            }
            x[low] = temp;
        }

        for (int i = 0; i < x.length; i++) {
            System.out.println(x[i]);
        }

希尔排序（适用较大规模无序数据）

基本思想：通过分组排序避免大规模数据的遍历

实现：

对于{15,8,95,63,45,67,26,58}个树，希尔排序先根据增量序列进行分组，假设第一次增量为8/2=4.

那么分完组就是{15,45}，{8,67}，{95，26}，{63,58}一共四组，每组内部进行排序，比如{15,45}就不用排

然后{95,26}排序为{26,95}。

第一次排序结果为{15，8 ,67,58,45,95,26,63}

增量为4/2=2

分组为{15,67,45,26}，{8,58,95,63}

组内进行排序

第二次排序结果为：{15,26,45,67,8,58,63,95}

增量为2/2=1

直接排序

第三次排序结果：{8,15,26,45,58,63,67,95}


希尔排序的复杂度和增量序列是相关的

{1,2,4,8,...}这种序列并不是很好的增量序列，使用这个增量序列的时间复杂度（最坏情形）是O(n^2)

Hibbard提出了另一个增量序列{1,3,7，...,2k-1}，这种序列的时间复杂度(最坏情形)为O(n1.5)

Sedgewick提出了几种增量序列，其最坏情形运行时间为O（n^1.3）,其中最好的一个序列是{1,5,19,41,109,...}


直接插入排序和二分查找排序在小规模数据且基本有序的情况下比较高效。

希尔排序在大规模数据且无序的情况下高效。

/**
         * 希尔排序
         */
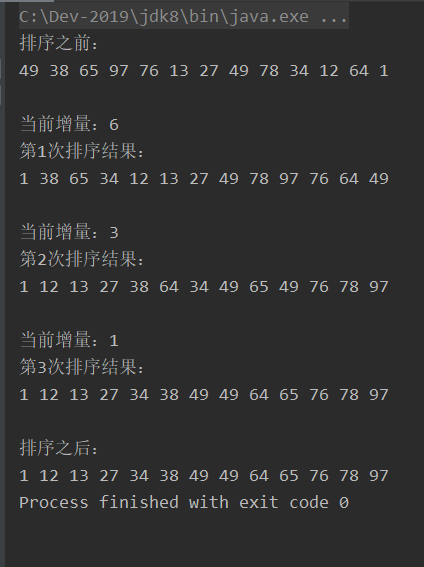
        int[] x= new int[]{49,38,65,97,76,13,27,49,78,34,12,64,1};
        System.out.println("排序之前：");
        for(int i=0;i<x.length;i++){
            System.out.print(x[i]+" ");
        }
        System.out.println();

        int gap = x.length;

        int count =1;
        while (true) {
            gap = gap/2;   //增量每次减半


            for (int i = 0; i < gap; i++)
            {
                for (int j = i + gap; j < x.length; j = j+ gap) {
                    int temp = x[j];
                    int k = j - gap;
                    while (k >= 0 && x[k] > temp) {
                        x[k + gap] = x[k];
                        k =k- gap;
                    }
                    x[k + gap] = temp;
                }
            }

            System.out.println();
            System.out.println("当前增量："+gap);
            System.out.println("第"+count+"次排序结果：");
            for(int m=0;m<x.length;m++){
                System.out.print(x[m]+" ");
            }
            System.out.println();
            count++;
            
            if (gap == 1)
            { break;}
        }
        System.out.println();
        System.out.println("排序之后：");
        for(int i=0;i<x.length;i++){
            System.out.print(x[i]+" ");
        }

1570614582391

从大至小输出：

 while (k >= 0 && x[k] < temp)

交换排序

冒泡排序

基本思想：比较相邻的元素，如果第一个比第二个大，元素交换（按照升序排列）

/**
         * 冒泡排序
         */
        int[] x = new int[]{49, 38, 65, 97, 76, 13, 27, 49, 78, 34, 12, 64, 1};

        for (int i = 1; i < x.length; i++) {
            for (int j = 0; j < x.length - i; j++) {
                if (x[j] < x[j + 1]) {
                    int temp = x[j];
                    x[j] = x[j + 1];
                    x[j + 1] = temp;
                }
            }

        }
        for(int i=0;i<x.length;i++){
            System.out.print(x[i]+" ");
        }

快速排序

1、先从数列中取出一个数作为基准数

2、分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边

3、再对左右区间重复第二步，直到各区间只有一个数

 public static void main(String[] args) {
        int[] arr = {1, 4, 5, 67, 2, 7, 8, 6, 9, 44};

        quickSort(arr, 0, arr.length-1);


        for(int i=0;i<arr.length;i++){
            System.out.print(arr[i]+" ");
        }


    }

    /**
     * 快速排序
     *
     * @param arr
     * @param L   指向数组第一个元素
     * @param R   指向数组最后一个元素
     */
    public static void quickSort(int[] arr, int L, int R) {
        int i = L;
        int j = R;

        //基准点
        int pivot = arr[(L + R) / 2];

        System.out.println("基准点为"+pivot);

        //左右两端进行扫描，只要两端还没有交替，就一直扫描
        while (i <= j) {

            //寻找直到比支点大的数
            while (pivot > arr[i])
            {i++;}

            //寻找直到比支点小的数
            while (pivot < arr[j])
            {j--;}

            //此时已经分别找到了比支点小的数(右边)、比支点大的数(左边)，它们进行交换
            if (i <= j) {
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;

                i++;
                j--;
            }
        }
        //上面一个while保证了第一趟排序支点的左边比支点小，支点的右边比支点大了。


        //“左边”再做排序，直到左边剩下一个数(递归出口)
        if (L < j)
        {quickSort(arr, L, j);}

        //“右边”再做排序，直到右边剩下一个数(递归出口)
        if (i < R)
        {quickSort(arr, i, R);}
    }

选择排序

直接选择排序

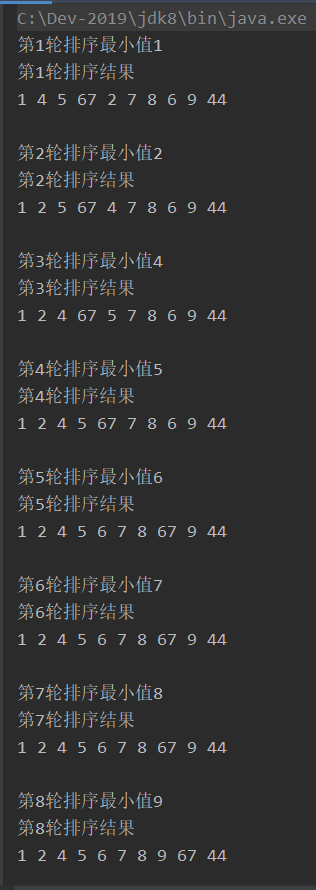
第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推。

int arr[] = new int[] {1, 4, 5, 67, 2, 7, 8, 6, 9, 44};

        for (int i = 0; i < arr.length - 1; i++) {
            int  min = i;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[min] > arr[j]) {
                    min = j;
                }
            }
            if (min != i) {
                int tmp = arr[min];
                arr[min] = arr[i];
                arr[i] = tmp;
            }
            System.out.println("第"+(i+1)+"轮排序最小值"+arr[i]);
            System.out.println("第"+(i+1)+"轮排序结果");
            for(int m=0;m<arr.length;m++){
                System.out.print(arr[m]+" ");
            }
            System.out.println();
            System.out.println();
        }

1570679899878

堆排序

堆排序过程

　1、构造堆，此时最大值就是堆的顶端

　　2、将顶端的数和末尾的数交换，固定最大值，然后将剩余的数重新构造堆

​ 3，重复上述过程

  public static void main(String[] args) {
        int[] array = new int[] { 66,54,87,94,53,25,44,87,76,68,92};

        sort(array);   //建堆，排序

        System.out.println(Arrays.toString(array));
    }

    public static void sort(int[] array) {
        /**
         * 为什么只需要遍历一半的数组？
         *
         * 堆使用索引计算的方式代替了指针：按照索引的规则，只有0到arr.length、2-1的节点范围内才存在父节点
         */

        System.out.println("建堆：将数组映射为二叉树：");
        for (int i = array.length / 2 - 1; i >= 0; i--) {

            //adjustHeap对于单个父节点进行建堆，调整
            adjustHeap(array, i, array.length);
        }

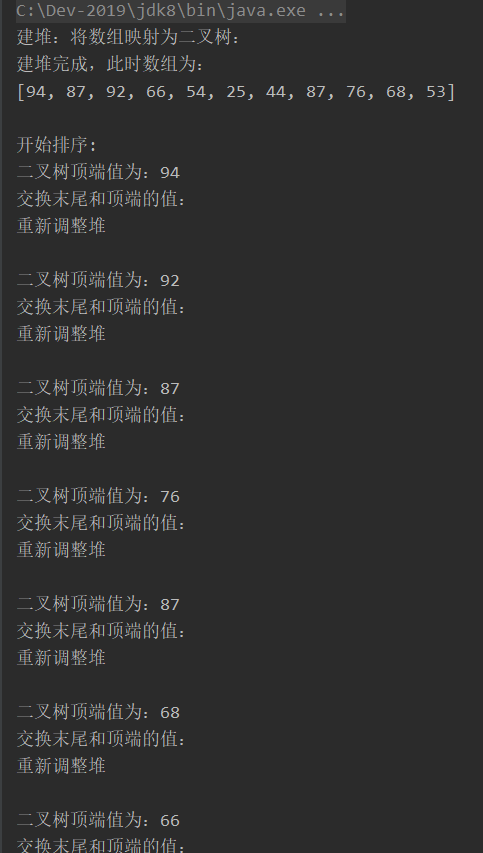
        System.out.println("建堆完成，此时数组为：");
        System.out.println(Arrays.toString(array));


        System.out.println();
        System.out.println("开始排序:");
        /**
         * 排序
         * 建堆完成之后，数组的第一个元素就是最大值
         */
        for (int j = array.length - 1; j > 0; j--) {

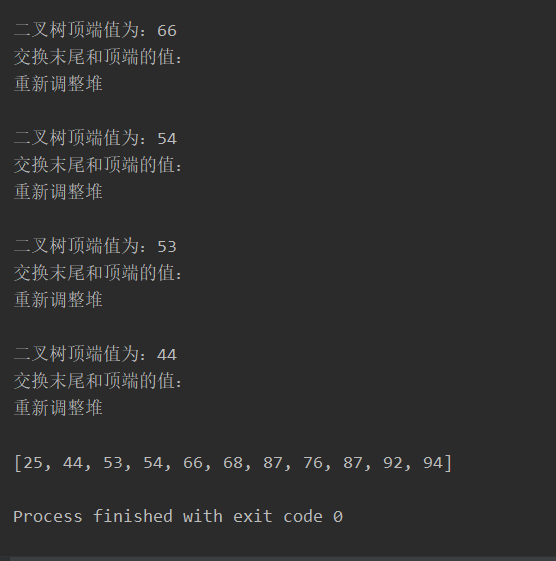
            System.out.println("二叉树顶端值为："+array[0]);

            // 将数组中最大值也就是index为0的值和末尾的值进行交换
            System.out.println("交换末尾和顶端的值");
            swap(array, 0, j);

            // 末尾值和最大值替换后需要重新调整堆，获取最大值
            System.out.println("重新调整堆");
            System.out.println();
            adjustHeap(array, 0, j);
        }
    }

    /**
     *   adjustHeap对于单个父节点进行建堆，调整
     */
    public static void adjustHeap(int[] array, int i, int length) {

        //temp为某个父节点
        int temp = array[i];

        //k下标代表父节点的左子节点
        for (int k = 2 * i + 1; k < length; ) {  //for循环：循环当前父节点及其子树的顺序

            //按照索引规则，父节点的左子节点和右子节点的规则是2i+1和2i+2,也就是说，k和k+1是父节点的两个子节点
            if (k + 1 < length && array[k] < array[k + 1]) {
                k++;
            }

            // 如果左右子节点中任意一个大于父节点的值，则进行节点交换
            if (array[k] > temp) {
                swap(array, i, k);

                // 如果子节点和父节点更换，那么父节点新的位置的子节点同样需要进行判断，交换
                //将子节点的下标赋值给父节点，继续循环
                i = k;
            } else
                {
                break;
                }
        }
    }

    /**
     * 进行节点间的交换
     */
    public static void swap(int[] arr, int a, int b) {
        int temp = arr[a];
        arr[a] = arr[b];
        arr[b] = temp;
    }

1570686086725

1570686095003

归并排序

归并排序的基本思想是将两个或者两个以上的有序序列归并成一个有序序列。

可以分为二路归并排序和多路归并排序。

计数排序

桶排序

基数排序

posted @ 2019-11-07 21:09  笑谈渴饮匈奴血  阅读(1266)  评论(0)  编辑  收藏  举报