经典排序算法--简单选择排序

算法简介

简单选择排序是一种选择排序。

选择排序：每趟从待排序的记录中选出关键字最小的记录，顺序放在已排序的记录序列末尾，直到全部排序结束为止。

白话理解

　　依然已排队为例，在排队时，有的老师可能会选择这样排序，先在一列中选出最矮的，放在第一位，然后选出第二矮的，放在第二位。队伍完成排序。而这就是选择排序的思想。

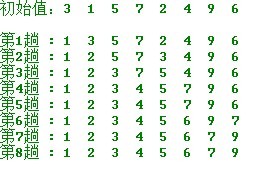
简单排序处理流程

(1)从待排序序列中，找到关键字最小的元素；

(2)如果最小元素不是待排序序列的第一个元素，将其和第一个元素互换；

(3)从余下的 N - 1 个元素中，找出关键字最小的元素，重复(1)、(2)步，直到排序结束。

Java代码实现：

package sortDemo;

/**
 * 插入代码实现
 * @author xianyu
 * @CreatTime 下午8:16:11
 */
public class SelectionDemo {
    
    public static void main(String[] args) {
        int[] sort ={3,2,1,4,6,5,8,9,10,7} ;
        System.out.println("排序前：");
        print(sort);
        selectionDemo(sort);
        System.out.println("\n排序后：");
        print(sort);
    }
    
    public static void selectionDemo(int[] a){
        for (int i = 0; i < a.length; i++) {
            for (int j = i+1; j < a.length; j++) {
                if(a[j]<a[i]){
                    int tmp = a[j];
                    a[j] = a[i];
                    a[i]=tmp;
                }
            }
        }
    }
    
    public static void print(int[] a){
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+" ");
        }
    }
}

算法分析：

时间复杂度

简单选择排序的比较次数与序列的初始排序无关。 假设待排序的序列有 N 个元素，则比较次数总是N (N - 1) / 2。

而移动次数与序列的初始排序有关。当序列正序时，移动次数最少，为 0.

当序列反序时，移动次数最多，为3N (N - 1) /  2。

所以，综合以上，简单排序的时间复杂度为 O(N2)。 

空间复杂度

简单选择排序需要占用 1 个临时空间，在交换数值时使用。

 

由交换条件，a[j+1]<a[i]可以判断出，相同的值并不会交换。所以简单选择排序是稳定排序。

简单选择排序的改进——二元选择排序

简单选择排序，每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素（当前趟最大和最小记录）的位置,从而减少排序所需的循环次数。改进后对n个数据进行排序，最多只需进行[n/2]趟循环即可。具体实现如下：

static void selectSort(int[] r) {  
        int n = r.length;
        int i ,j , min ,max, tmp;  
        for (i=0 ;i <= n/2;i++) {    
            // 做不超过n/2趟选择排序   
            min = i; max = i ; //分别记录最大和最小关键字记录位置  
            for (j= i+1; j<= n-1-i; j++) {  
                if (r[j] > r[max]) {   
                    max = j ; continue ;   
                }    
                if (r[j]< r[min]) {   
                    min = j ;   
                }     
          }    
          //该交换操作还可分情况讨论以提高效率  
          tmp = r[i]; r[i] = r[min]; r[min] = tmp;  
          tmp = r[n-1-i]; r[n-1-i] = r[max]; r[max] = tmp;   
        }   
    }