简单约数

当然是重要的图片：

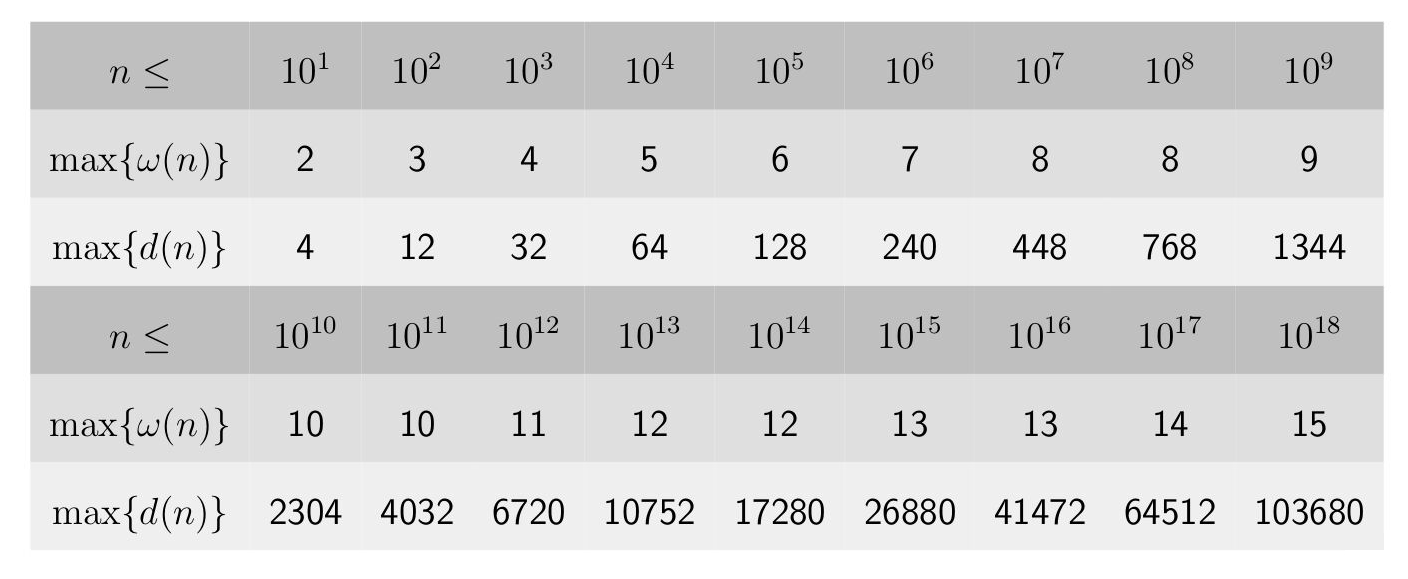
关于约数

若整数 $n$ 除以整数 $d$ 的余数为 $0$，即 $d$ 能整除 $n$，则称 $d$ 是 $n$ 的约数，记作 $d | n$。

算数基本定理推论

在算数基本定理中：若正整数 $N$ 被唯一分解为 $N = p_1^{c_1} p_2^{c_2} \cdots p_m^{c_m}$，其中 $c_i \in \mathbb{Z}, p_i \in \mathbb{P}, p_1 \lt p_2 \lt \cdots \lt p_m$，则 $N$ 的正约数集合可写作：

$N$ 的正约数个数为（可用乘法原理证明）：

$$\prod_{i = 1}^{m} (c_i + 1)$$

$N$ 的所有正约数之和为：

$$\prod_{i = 1}^{m} \left( \sum_{j = 0}^{c_i} (p_i)^{j} \right)$$

求正约数集合

求 $N$ 的正约数集合

类似试除法：

void DivideNum(const int n) {
    if (n % i == 0) {
        fac[++m] = i;
        if (i != n / i)
            fac[++m] = n / i;
    }
}

由此我们得到一个推论：

一个整数 $N$ 的约数个数上限为 $2 \sqrt{N}$。

求 $[1, N]$ 每个数的正约数集合

如果枚举 $1 \sim N$ 试除法变成 $O(N \sqrt{N})$ 显然太慢了，换个思路：$1 \sim N$ 中以 $d$ 为约数的数就是 $d$ 的倍数 $1d, 2d, 3d, \dots$：

std::vector<int> fac[N];
void DivideNum(const int n) {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n / i; j++)
            fac[i * j].push_back(i);
    }
}

复杂度是调和级数 $O(N \log N)$ 的。

由此我们可以得到一个新的推论：

$1 \sim N$ 每个数的约数个数的总和大约为 $N \log N$。

最大公约数、最小公倍数

不加证明地给出一些定理，证明并不困难，大多可以通过定义和同余的推论来验证：

• $$\forall a, b \in \mathbb{N}, \gcd(a, b) \times \text{lcm}(a, b) = a \times b$$

• 更损相减术

  • $$\forall a, b \in \mathbb{N}, a \geq b, \gcd(a, b) = \gcd(b, a - b) = \gcd(a, a - b)$$

  • $$\forall a, b \in \mathbb{N}, \gcd(2a, 2b) = 2 \gcd(a, b)$$

• 欧几里得算法

  • $$\forall a, b \in \mathbb{N}, b \neq 0, \gcd(a, b) = \gcd(b, a \bmod b)$$

  • 复杂度是 $O(\log(a + b))$ 的，是最常用的求解 gcd 的方法。在高精度除法中可以考虑使用更损相减术来代替欧几里得算法