第3章：有限马尔科夫决策过程

1.Agent-Environment接口

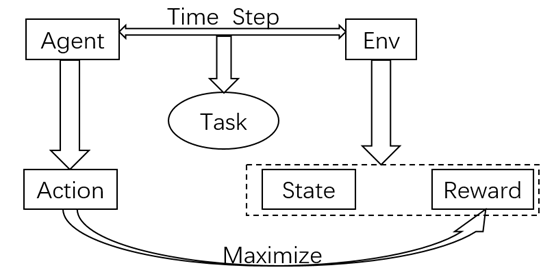
　　Agent是学习者和决策制定者，环境是由一切Agent之外的东西组成。下图是马尔科夫决策过程的agent和environment交互过程。

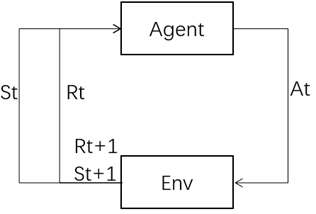
　　如果说一个状态包含关于过去agent-env交互的全部信息，并且这个交互会对未来造成一定的影响，那么称这个状态具有马尔科夫性质。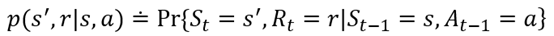

 

 

MDP的dynamics 概率等式p

2.目标和奖励

　　通常，我们agent的目标是使它接收到的累积奖励最大。这就意味着并不是去最大化眼前的奖励，还是最大化整个过程中的奖励。奖励也是区分强化学习的最显著地特点之一。

　　我们设置的奖励应该是使agent能够达到我们的目标，而不是能够学会以什么样的方式来达到我们的目标。比如说，我们在下象棋的时候，agent可能会想着去吃掉对方的棋子，哪怕付出的代价是输掉这场比赛。这就是如何正确设置奖励的重要性，它的设立应该是为实现我们的目标而服务的，而不是以什么样的方式去实现。

3.返回值和片段

　　在简单的场景下，返回值是所有奖励的总和。Gt= Rt+1 + Rt+2 + Rt+3 + Rt+4 +......+RT;

　　但是如果说在有些场景系，片段不是有有限的步骤，而是无限的。为了解决这种情况，就引入了折扣因数 γ，γ是个小于等于1的数。当γ小于1的时候，无限步数Gt就会有一个有限的值；当γ等于0的时候，就表示agent只关心眼前的奖励。但是，通常情况下，只关心眼前的奖励会减少获得未来奖励的可能性。当γ接近1的时候，agent把未来的奖励也考虑进去，这个时候就会很有远见。

4.策略和值函数

　　值函数（状态值函数或者是状态动作值函数）：评估agent在给定的状态下的好坏；或者是在给定的状态下，执行给定的动作的好坏。

　　策略：根据特定的动作来决定值函数，就是策略。一个策略就是一个从状态到各个动作可能性的映射。

　　其中最重要的是贝尔曼方程，这个是整个强化学习值函数的基本性质。

 

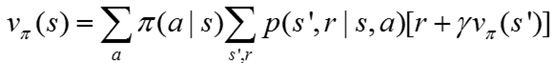
 　　上面就是Vπ的贝尔曼方程，他表示的是当前状态值和下一个状态值之间关系。

 

 

 

 

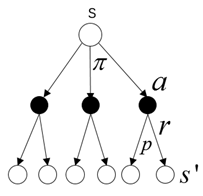
Backup diagram for vπ

 

 　　通过Backup diagram  可以很清楚理解贝尔曼方程的原理。空心圆代表的是状态，实心圆代表的是状态-动作对。

　　

                            

 

 

 

 

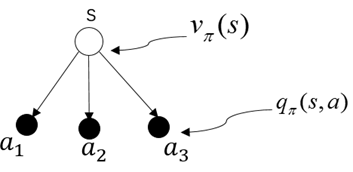
                状态值函数vπ（s）                                                                                    状态-动作值函数qπ（s,a）                         

  　　这两个图表明了状态值函数和状态-动作值函数之间的关系

5.总结

agent通过episode 中的每一步和环境进行交互，两者共同组合成一个任务task，agent 的action是以最大化整个阶段的reward总和为目的，其中state 和 reward 是归环境所有，和agent没有任何关系。