期望概率DP总结
主要是codeforces上的。
在这道题发现一个重要的问题,当题目输出精度有较高要求时,输出多位,比如这道题里出现了1e-9,那么输出10位小数。
这道题输出同样需要使用printf输出更多的小数位,cout真的不能再用了
f[i][j]表示公主面对还剩下i个白色老鼠,j个黑色老鼠的局面获胜的概率。根据题意进行转移。
http://poj.org/problem?id=2151
f[i][j][k]:表示第  i 个队在前 j 题中做对 k 道的概率。
所有队都至少做出一道题且至少有一个队做出了 n 道题,这个限制正向不好做,考虑反向容斥。
将所有队的问题转化为两部分,一个是所有队都至少做出一道题,一个是所有队在都至少做出一道题的基础上,每队都只做了<n的题数,两者相减,就是问题的答案。
背包dp+概率。
求被抓概率,和不被抓概率都行。
UVA11762 Race to 1
多组数据,但是n的范围1e5,直接一个一个求就行,x的约数数量只有<=sqrt(x)个,直接dp就行。
P1654 OSU!
经典的概率增量贡献,有多种方法思考。
The 2024 CCPC Online Contest - E.随机过程 Codeforces

注意一个问题,对于后面的人,他的贡献是在前面的人都上去的基础上的,不能够只考虑他自己上电梯的概率p,还必须考虑他前面的人上去的概率,前面的人全上去的概率与使用的时间有关,所以dp的状态需要加一维时间,第二维是人数。
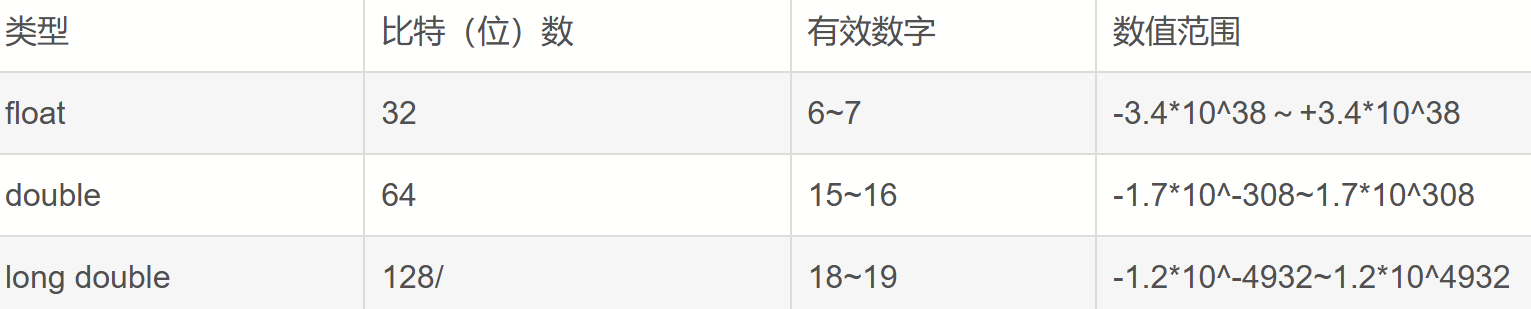
这道题里,出现了非常大的C(n,m),并且要求小数输出,此时不用担心精度问题,因为答案是一个小数而且精度要求不高,只需要担心数值范围是否够用,开成long double完全没有问题。
经典树上期望,求每个点的期望到达时间。
积分的时候注意第二维的参数的取值范围,它有两个限制条件,必须全部满足。
画个坐标系可以发现,根据a,b的大小,直线x=4y与随机区域的相交形式不同。
总结:
1.利用期望的定义,E(Y)=sum( p[k]*k )。
单点贡献。考虑每个单点对总体的贡献,求出单点的概率乘上单点的贡献,就是总贡献。
直接求P(k)比较难求的时候,可以尝试求P(>=k),相减就可以。
使用二项式反演:
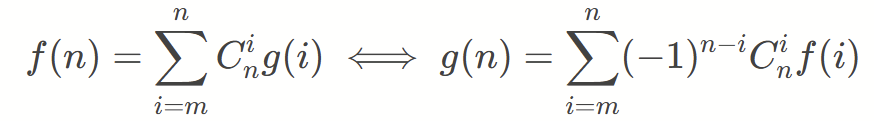
2.dp处理。


