[2020.11.13]UOJ#424. 【集训队作业2018】count

题意

求有多少种合法的笛卡尔树使得它对应至少一个长度为\(n\)，所有数都在\(1\)到\(m\)之间且每个数出现至少一次的序列。

题解

首先，如果\(m>n\)那么答案为\(0\)

否则可以证明只要一棵笛卡尔树对应一个所有数都\(\le m\)的序列，一定能对应一个所有数至少出现一次的序列。

考虑贪心判断一棵笛卡尔树是否合法，那么对于任意子树，左侧节点值为根\(+1\)，右侧节点值为根。

所以以可笛卡尔树是否合法，取决于从根走到任意叶子，往左次数的最大值是否\(\le m\)。

考虑dfs这颗笛卡尔树的过程，每次一定是从当前节点往左走一步，或者向上跳若干步（可以为\(0\)）然后向右走。

于是我们可以得到一个DP:

设\(f_{i,j}\)表示当前在dfs序上第\(i\)个节点，从根到该节点的路径上向左走了\(j\)次。那么容易得到转移：

\[f_{i,j}=\sum_{k=\max(0,j-1)}^mf_{i-1,k} \]

观察这个式子，发现如果我们记根到dfs序上第\(i\)个节点的路径上向左走的次数为\(a_i\)，那么其实答案就是满足以下条件的\(a\)序列的数量：

• \(a_1=0\)
• \(0\le a_i\le m\)
• \(a_i\le a_{i-1}+1\)

这个东西不好统计，那么我们可以令\(p_i=i-a_i\)，那么合法的\(p\)的条件是：

• \(p_1=1\)
• \(i-m\le p_i\le i\)
• \(p_i\ge p_{i-1}\)

我们类似这个题，将\(p_i\)画成柱状图。

于是问题变成求从\((0,1)\)开始向右上走，不能碰到\(y=x+2\)和\(y=x-(m+1)\)，走到以\((n-1,\max(1,n-(m+1)))\)和\((n-1,m)\)为端点的线段上的方案数。

走一条线段的方案数相当于走到所有点的方案数和，可以发现是形如\(\binom{x+i}{y+i}\)形式的和，可以\(O(1)\)算。

剩下的问题就是如何统计不和上、下直线相交的方案数。

我们可以算总方案减去不合法方案，所以现在我们要设计一个计数方法，使得每一种不合法路径被计算恰好一次。

考虑如下路径：

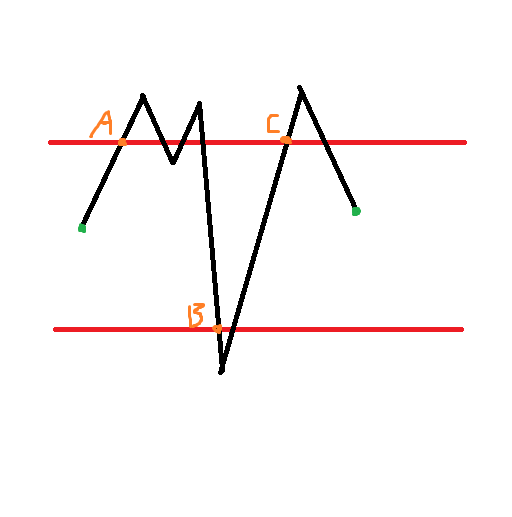
我们可以在它第一次经过上边界（A）时计入\(1\)的贡献，然后经过下边界（B）时计入\(-1\)的贡献，再经过上边界（C）时计入\(1\)的贡献；

然后反过来，第一次经过下边界（B）时计入\(1\)的贡献，然后经过上边界（C）时计入\(-1\)的贡献。

然后？

我们发现它在A处产生了恰好为\(1\)的贡献，其他位置没有产生贡献。

于是我们可以考虑这样计数，计算经过上边界的方案数并产生\(1\)的贡献，再计算先经过上边界然后经过下边界的方案数并产生\(-1\)的贡献，以此类推。然后反过来先计算经过下边界即可。

但是如何计算先经过上边界，再经过下边界的方案数呢？

首先计数经过上边界，直接将一个端点对称到上边界另一侧：

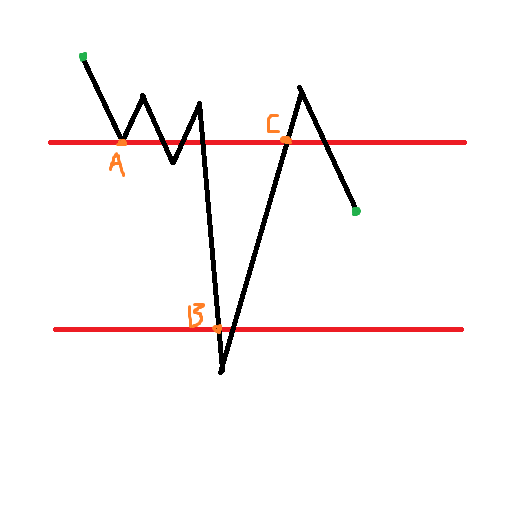
然后再计数先经过上边界再经过下边界，将一端对称到下边界另一侧：

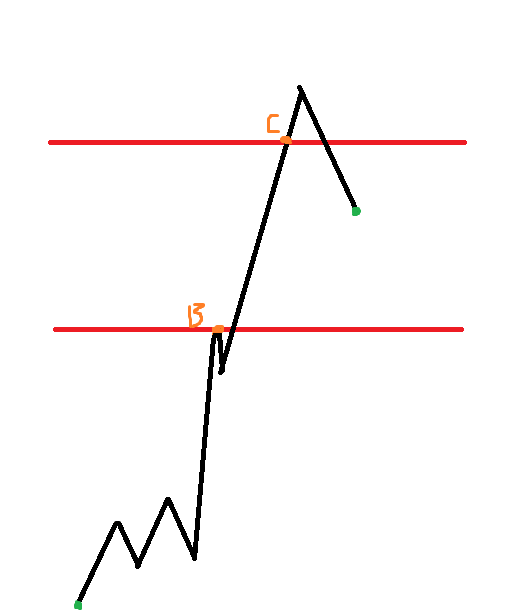
然后以此类推，求上-下-上时就将一端对称到上边界另一侧即可。

重复上述步骤直到不存在从一端到另一端的路径。

时间复杂度应该是\(O(n+m)\)的？

code:

#include<bits/stdc++.h>
#define ci const int&
#define C(x,y) (y>=0&&x>=y?1ll*fac[x]*invf[y]%mod*invf[x-(y)]%mod:0)
using namespace std;
const int mod=998244353;
int n,m,fac[400010],invf[400010],ans,px,py,pt,tg;
int POW(int x,int y){
	int ret=1;
	while(y)y&1?ret=1ll*ret*x%mod:0,x=1ll*x*x%mod,y>>=1;
	return ret;
}
int Sum(ci x,ci y,ci num){
	return(C(x+num+1,y+num)-C(x,y-1)+mod)%mod;
}
int Calc(ci x,ci y,ci t,ci tg){
	if(tg)return Sum(x+y,x,t-x);
	else return Sum(x+y,y,t-y);
}
int main(){
	scanf("%d%d",&n,&m),--m,fac[0]=1;
	if(m>=n)return putchar('0'),0;
	for(int i=1;i<=(n+m<<1);++i)fac[i]=1ll*fac[i-1]*i%mod;
	invf[n+m<<1]=POW(fac[n+m<<1],mod-2);
	for(int i=(n+m<<1)-1;i>=0;--i)invf[i]=1ll*invf[i+1]*(i+1)%mod;
	px=n-1,py=max(0,n-m-1),pt=n-1,tg=0,ans=mod-Calc(px,py,pt,tg);
	for(int i=1,op=1;tg?px<=pt&&py>=0:py<=pt&&px>=0;i^=1,op=mod-op){
		ans=(ans+1ll*op*Calc(px,py,pt,tg))%mod,tg^=1;
		if(tg)--pt,swap(px,py),px=max(px-1,0),++py;
		else pt-=m+2,swap(px,py),px+=m+2,py=max(py-(m+2),0);
	}
	px=n-1,py=max(0,n-m-1),pt=n-1,tg=0;
	for(int i=1,op=1;tg?px<=pt&&py>=0:py<=pt&&px>=0;i^=1,op=mod-op){
		ans=(ans+1ll*op*Calc(px,py,pt,tg))%mod,tg^=1;
		if(tg)pt+=m+2,swap(px,py),px+=m+2,py-=m+2;
		else ++pt,swap(px,py),--px,++py;
	}
	printf("%d",ans);
	return 0;
}