从Unit Bezier的实现学习两种经典数值求解算法
近年来的UI设计开始越来越多地注重“动画曲线”的应用。这个网站展示了常用的动画曲线,可以直观感受到它相比于线性动画能带来更好的视觉效果。
目前主流的UI框架都支持此类动画曲线,例如CSS的animation-timing-function属性。甚至最新的Windows 11的窗口动画也用上了。
它们的底层实现利用的正是在计算机图形领域应用非常广泛的贝塞尔曲线(Bezier Curve)。
具体来说,动画曲线采用的是带约束的Cubic Bezier,第一个控制点A和最后一个控制点D分别固定在(0,0)和(1,1)的坐标,而中间两个控制点B和C位于区间0<=x,y<=1(某些框架允许xy超出标准区间,这里不做讨论)。因为坐标都限制在[0,1]区间内,因此它也被称为Unit Bezier。通过修改Bx,By,Cx,Cy四个数值,即可自定义一个新的动画曲线。
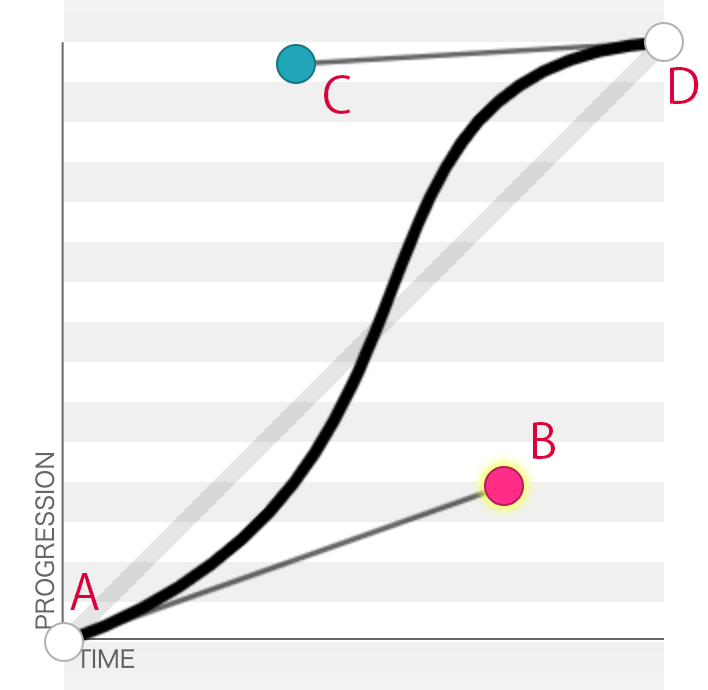
Unit Bezier是关于0<=t<=1的参数曲线(注意t不是time),x轴是时间,y轴是动画进度:
\(x(t)=3(1-t)^2 t B_x + 3(1-t)t^2 C_x + t^3\)
\(y(t)=3(1-t)^2 t B_y + 3(1-t)t^2 C_y + t^3\)
那么问题来了:给定一个时间x,如何求出动画进度y?
如果我们知道参数t,那么就能通过公式直接求出y。但是如何先通过x反过来求t呢?
x(t)是一个一元三次方程,我们可以利用求根公式来求解,但是计算会比较复杂。实际上对于计算机求(近似)解我们有更通用的办法。
Unit Bezier的单调性
注意到BC都在区间[0,1]内,不断挪动BC的位置后(可以通过这个网站试试),我发现一个规律:曲线始终是单调递增的。
要证明这一点,等价于证明Unit Bezier的偏导数x'(t)和y'(t)都非负。由于两者公式一样,仅以x'(t)为例:
\(x'(t)=(1-t)(3-9t)B_x+t(6-9t)C_x+3t^2\geq0\)
这是一个带约束的三元非线性方程,直接证明需要大量的数学工作,但是利用计算机枚举我们可以偷偷懒:
[Python]
minval = float('inf') samples = [x / 100.0 for x in range(0, 101)] for t in samples: for Bx in samples: for Cx in samples: minval = min(minval, (1-t)*(3-9*t)*Bx+t*(6-9*t)*Cx+3*t*t) print(minval)
结果是0.0.
曲线的递增特性,给我们求解打开了许多可能性。
代码实现
下面看看Safari浏览器的开源引擎WebKit是怎么解决这个问题的。
直接上代码(完整源码在这里):
// Given an x value, find a parametric value it came from. double solveCurveX(double x, double epsilon) { double t0; double t1; double t2; double x2; double d2; int i; // First try a few iterations of Newton's method -- normally very fast. for (t2 = x, i = 0; i < 8; i++) { x2 = sampleCurveX(t2) - x; if (fabs (x2) < epsilon) return t2; d2 = sampleCurveDerivativeX(t2); if (fabs(d2) < 1e-6) break; t2 = t2 - x2 / d2; } // Fall back to the bisection method for reliability. t0 = 0.0; t1 = 1.0; t2 = x; if (t2 < t0) return t0; if (t2 > t1) return t1; while (t0 < t1) { x2 = sampleCurveX(t2); if (fabs(x2 - x) < epsilon) return t2; if (x > x2) t0 = t2; else t1 = t2; t2 = (t1 - t0) * .5 + t0; } // Failure. return t2; }
给定x,这个函数返回满足精度误差<epsilon的t。
这个函数里面用到了两个非常经典,也非常简单的数值求解算法:
1、牛顿法(Newton's Method)
我们先“猜测”一个解t2=x,然后算出t2处的x(t2)和导数d2。
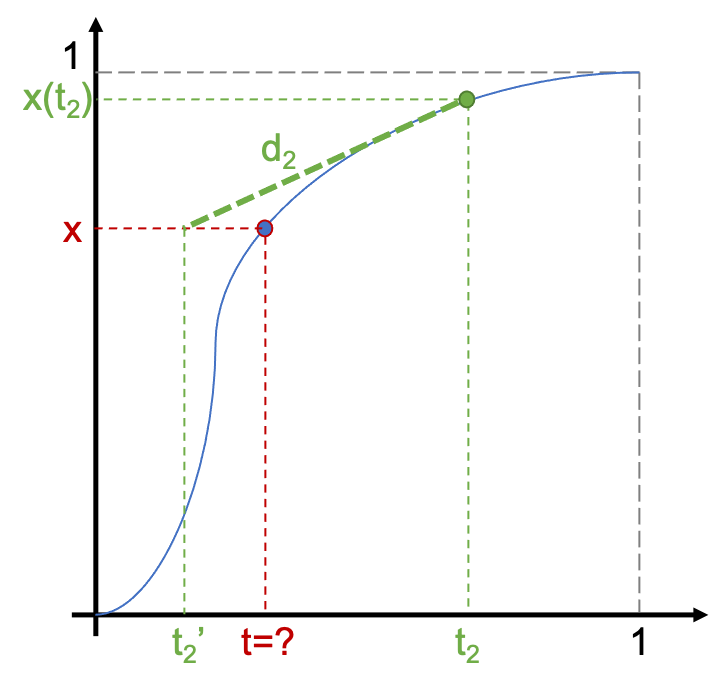
我们可以合理地假定曲线是局部线性的,根据以上结果更新t2的值,使其更逼近t:
\({t_2}'=t_2-(x(t_2)-x)/d_2\)
不断迭代更新t2的值,我们能大概率地在有限次数内求解出足够逼近t的近似解。
2、二分法(Bisection Method)
由于曲线是单调递增的,我们也可以采用大家都广为熟知的二分法来求t:
1. 初始化t区间[t0=0,t1=1], t2=x
2. 求出x(t2)
3. 若x(t2)足够逼近x,返回t2;否则比较x(t2)与x的大小关系,更新t区间为[t0,t2]或者[t2,t1],更新t2为区间中点,继续2
两种方法之中,二分法更健壮,但牛顿法更高效,因此代码中结合了两者,先尝试高效求解,不行再回退更稳妥的方法。这也是一种很常见的优化策略。
两种方法都用很广泛的应用,例如对贝塞尔进行等距采样,还有另一个经典的例子是求一个数的平方根(sqrt)。
相关链接
- 牛顿法的数学原理
- Chromium的实现(基本一样,但是处理了[0,1]区间外的情况)
- A Primer on Bézier Curves



