11.4 - 12.31

11.4 - 12.31 改题纪要

NOIP2024模拟1

不是每个题都有乱搞过得是吧。

1. T1 玩游戏

   先前缀和，问题变成 $a_i+b_j\le 0$

   考虑显然贪心，每次移动到更优的位置。

   这样可以跳到最小的位置，发现到终点和从起点跳过来是类似的，倒着跑一遍即可。

2. T2 排列

   首先发现当 $k>\log n$ 时一定无解 因为显然每次最少消掉一半。

   考虑 dp。

   发现对于最大值可以将数组分成不相干的两部分，考虑直接在笛卡尔树上跑。

   除了要特判的根，对于一个子树，其只有两种可能：有一边有最大值和两边都有最大值。设 $d{p}_{i,j,0/1}$ 表示大小为 $i$，总共 $j$ 步消完，$0/1$ 表示不同种子树。

   转移挺显然，暴力整是 $n^2{\log }^{2}n$ 的，加上巴雷特约减轻松过，前缀和优化一下可以做到 $n^2\log n$ 的。

3. T3 最短路

   好题。

   首先那个二维 dij 是假的了。

   考虑最后走的路线一定是一些环接起来，顺逆时针依次颠倒。环的交就是重合的点。

   设 $d{p}_{i,j}$ 表示 $1\to i\to j\to 1$ 的最短距离，类似 dij 暴力枚举其后面两个 $i^{\prime },j^{\prime }$ 可以做到 $n^4\log n$。

   发现的转移贡献 $j\to i^{\prime }\to j^{\prime }\to i$ 中 $i^{\prime }\to j^{\prime }\to i$ 和 $j$ 没有关系，可以设置一个中转状态 $f_{i,j}$ 表示 $d{p}_{i,k_1}\to dpj,k_2$ 中只计算了 $k_1\to j$ 的贡献的值，这个显然可以在 $d{p}_{i,k_1}$ 时枚举 $j$ 转移，然后用 $f_{i,j}$ 枚举 $k_2$ 转移 $d{p}_{j,k_2}$ 即可做到优秀的 $n^3\log n$ 复杂度。

   因为值域较小，可以用桶代替堆，做到 $n^3$，但是 $n^3\log n$ 已经可以通过。

4. T4 矩形

   起手扫描线。

   考虑线段树维护加线段和减线段，加线段时直接维护线段覆盖次数，并将覆盖的所有颜色推平，可以用并查集维护；减线段时打标记，当加线段时发现这段区间已经被减成 $0$ 了就新染颜色。

   发现只有加线段会新加常数个颜色段，一个颜色段只会贡献一次，复杂度显然。

多校A层冲刺NOIP2024模拟赛18

1. T4 银行的源起（banking）

   首先经典结论，树的重心和边权无关，只放一个点时总贡献是 $\sum _{\{u,v,w\}\in E}wmin(siz{e}_v,n-siz{e}_v)$。

   考虑放两个等价于断掉一条边，再在两棵树上分别选一个。

   将贡献拆开，问题就变成了求 $siz{e}_u\ge k$ 的和，断开一条边，发现只有到从根到这条边的链上的 $size$ 有变化，用东西维护一下链上的贡献，其他的贡献直接拆到 dfs 序上即可。

   链上的贡献可以用线段树维护，发现加一个点重心一定不上移，有单调性也可以维护栈二分。

NOIP2024加赛2

1. T4 灯笼

   这个确实是好题。

   首先考虑 $dp$，容易发现在任意时刻海拔区间都是连续的，因为你可以在要用的时候去买，对于每个起点，设 $d{p}_{i,j}$ 表示海拔区间是 $[i,j]$ 的最小花费，因为其一定包含这个起点，所以一定唯一确定一段可以行走的山脉，枚举下回买什么转移即可。

   对于每个起点单独做是没有前途的，发现终止坐标只有一个，考虑倒着转移，每次枚举当前买的是那个并且将他删掉并加入贡献。容易发现这样我们需要知道当前可行走山脉的一个点，是三维的，考虑记录贡献左右端点的灯笼，我们的区间一定经过这两个点，状态就只用设二维。

   现在的状态：$d{p}_{i,j}$ 表示海拔区间是 $[a_i,b_j]$ 的最小花费，转移懒得打了，贺了一个：

   

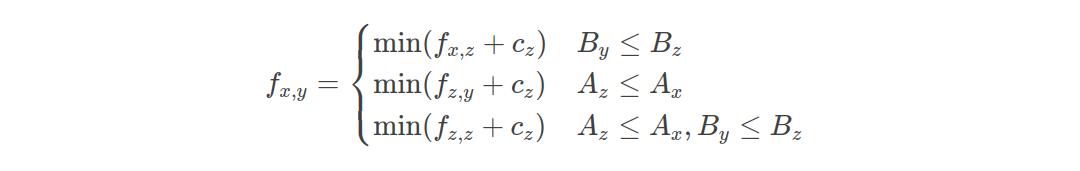
   考虑前两种情况，发现限制显然具有单调性，用个堆维护所有转移点即可。

   考虑第三种情况，发现我们可以让 $d{p}_{k,k}\to d{p}_{k,v}\to d{p}_{u,v}$，其中 $d{p}_{k,v}$ 本身并不是合法状态，我们钦定它等于 $d{p}_{k,k}$ 即可。

多校A层冲刺NOIP2024模拟赛19

1. T2 两棵树

   首先你会经典结论，森林的连通块数量等于 $\text{点数}-\text{边数}$ 然后发现可以直接拆贡献，然后你就会了。

2. T3 函数

   容易发现最靠后的正的和最靠后的负的中一定有一个是答案，直接 trie 上二分即可。

3. T4 编辑

   好题。

   首先你会 $n^3$ 暴力 $dp$。

   发现 $k$ 作为 $dp$ 的值却有非常优秀的性质，考虑将它设到状态里。

   设 $d{p}_{i,j}$ 表示更改 $i$ 次，两串长度之差为 $j$，能匹配的最大长度。

   每次转移时求 $lcp$ 尽量扩展这次的长度，再用这次转移，考虑下一次操作用什么即可。

多校A层冲刺NOIP2024模拟赛20

1. T2 和平精英

   你首先注意到 $\mathrm{\&}$ 不升，$|$ 不降，所以一定是将一些小的或起来等于一些大的与起来。

   发现一些更好的性质，$\mathrm{\&}$ 的 $popcount$ 不升，$|$ 的 $popcount$ 不降，所以直接枚举 $popcount$ 维护区间 $\mathrm{\&}|$ 即可。

2. T4 对称旅行者

   难题。

   考虑求最后的期望位置，设为 $f_i$。

   考虑每次的转移化简后是 $f_i=f_{i-1}+f_{i+1}-f_i$，其几何上相当于对 $f_{i-1},f_{i+1}$ 的中点做对称。

   考虑对称后到端点的距离，容易想到设 $g_i=f_{i+1}-f_i$，那么每次变换相当于交换 $g_i,g_{i+1}$。

   可以快速幂维护 $g$，而 $f_1$ 始终不变，可以直接求出所有 $f$。

NOIP2024（欢乐）加赛3

1. Long Way to be Non-decreasing

   求基环树上两点距离题。

   考虑先二分答案，check 时尺取从小到大枚举跳到哪，问题就变成了判断能否跳到，即基环树上距离是否 $\le k$。

NOIP2024加赛4

1. T1 王国边缘

   唐氏才想基环树。

   对我是唐氏。

   直接倍增即可。

2. T2 买东西题

   返回贪心板子。

   考虑先按 $a$ 和 $w$ 升序排序，这样遍历物品时优惠券是递增的，不会有删除。

   考虑对于一个物品，其肯定是选能用的中最大的优惠券，考虑到可能将这张优惠券留到后面给其他的会更优秀，于是可以将折扣价当成优惠券放到里面去，以后选了折扣价可以视为将优惠券换回来。

3. T4 魔法少女们

   好题：可以看 2024.11.12 鲜花

多校A层冲刺NOIP2024模拟赛21

1. T2 共轭树图

   就是你考虑经典结论，森林的联通块数等于点数减边数，然后你就直接会了。

2. T3 摸鱼军训

   考虑一次冒泡，如果前面有大于你的东西，其一定会跑到你后面，如果大于你的看成 $1$，小于的看成 $0$，容易发现其相当于是将前面的一个扔到最后了。

   考虑当前面没有大于你的时，你一次会向后走多少，依然看成 $01$，容易发现你是走到了第一个大于你的位置，并且将这段连续的 $1$ 中的最后一个扔到最后。

   考虑用数据结构维护这个，可以直接线段树二分。至于变成 $01$ 串，可以直接离线按值排序后扫描线。

3. T4 神奇园艺师

   其实就是一个范德蒙德卷积板子。

   考虑首先将分解质因数，对于每个质因数单独考虑。

   容易发现其相当于是对于每个子集求中位数，考虑当左边选 $i$ 个，右边选 $j$ 个时的贡献，暴力算是 $n^3$ 的。

   将式子写出来推一推发现是范德蒙德卷积板子，于是单次可以 $O(n)$，发现复杂度卡在最开始的一段 $0$ 上，其贡献是好算的，所以总复杂度是 $O(n\log n)$（如果用桶排）。

剩下的抽时间再说吧