网上关于六关节机器人运动学的资料很多,部分资料在坐标系法则上或是计算数据上存在错误,下面整理的程序已通过验证。
根据Denavit-Hartenberg方法:(Rot(z,θ)Trans(a,0,d)Rot(x,α)


另一种计算形式:

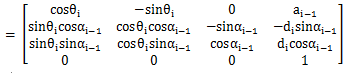
由第一种方式得到的六关节矩阵:

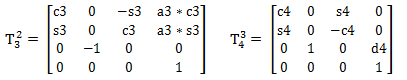
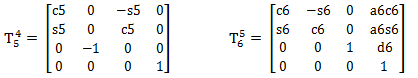
则:
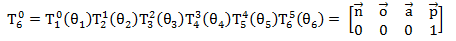
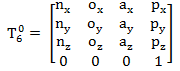
1 /// <summary> 2 /// 关节末端的空间姿态-位置向量[px,py,pz] 3 /// </summary> 4 /// <param name="AD">每个关节的a,d值构成的数组列表,如GSK RB8:{{150,0},{560,0},{155,0},{0,630},{0,0},{0,155}}</param> 5 /// <param name="Ang">每个关节的角度值</param> 6 /// <returns>[px,py,pz]</returns> 7 public static double[] R6P(List<double[]> AD, double[] Ang) 8 { 9 double A1 = AD[0][0]; 10 double D1 = AD[0][1]; 11 double A2 = AD[1][0]; 12 double A3 = AD[2][0]; 13 double D4 = AD[3][1]; 14 double A6 = AD[5][0]; 15 double D6 = AD[5][1]; 16 double C1 = Math.Cos(Ang[0]); 17 double S1 = Math.Sin(Ang[0]); 18 double C2 = Math.Cos(Ang[1]); 19 double S2 = Math.Sin(Ang[1]); 20 double C3 = Math.Cos(Ang[2]); 21 double S3 = Math.Sin(Ang[2]); 22 double S23 = Math.Sin(Ang[1] + Ang[2]); 23 double C23 = Math.Cos(Ang[1] + Ang[2]); 24 double C4 = Math.Cos(Ang[3]); 25 double S4 = Math.Sin(Ang[3]); 26 double C5 = Math.Cos(Ang[4]); 27 double S5 = Math.Sin(Ang[4]); 28 double C6 = Math.Cos(Ang[5]); 29 double S6 = Math.Sin(Ang[5]); 30 31 double px = ((C1 * S23 * C4 + S1 * S4) * C5 + C1 * C23 * S5) * A6 * C6 - (C1 * S23 * S4 - S1 * C4) * A6 * S6 - ((C1 * S23 * C4 + S1 * S4) * S5 - C1 * C23 * C5) * D6 + C1 * C23 * D4 + C1 * S23 * A3 + C1 * A2 * S2 + A1 * C1; 32 double py = ((S1 * S23 * C4 - C1 * S4) * C5 + S1 * C23 * S5) * A6 * C6 - (S1 * S23 * S4 + C1 * C4) * A6 * S6 + ((-S1 * S23 * C4 + C1 * S4) * S5 + S1 * C23 * C5) * D6 + S1 * C23 * D4 + S1 * S23 * A3 + S1 * A2 * S2 + A1 * S1; 33 double pz = (C23 * C4 * C5 - S23 * S5) * A6 * C6 - C23 * S4 * A6 * S6 - (C23 * C4 * S5 + S23 * C5) * D6 - S23 * D4 + C23 * A3 + A2 * C2 + D1; 34 return new double[] { px, py, pz }; 35 } 36 /// <summary> 37 /// 关节末端的空间姿态-n向量[nx,ny,nz] 38 /// </summary> 39 /// <param name="Ang">每个关节的角度值</param> 40 /// <returns>[nx,ny,nz]</returns> 41 public static double[] R6N(double[] Ang) 42 { 43 double C1 = Math.Cos(Ang[0]); 44 double S1 = Math.Sin(Ang[0]); 47 double C3 = Math.Cos(Ang[2]); 48 double S3 = Math.Sin(Ang[2]); 49 double S23 = Math.Sin(Ang[1] + Ang[2]); 50 double C23 = Math.Cos(Ang[1] + Ang[2]); 51 double C4 = Math.Cos(Ang[3]); 52 double S4 = Math.Sin(Ang[3]); 53 double C5 = Math.Cos(Ang[4]); 54 double S5 = Math.Sin(Ang[4]); 55 double C6 = Math.Cos(Ang[5]); 56 double S6 = Math.Sin(Ang[5]); 57 double nx = ((C1 * S23 * C4 + S1 * S4) * C5 + C1 * C23 * S5) * C6 - (C1 * S23 * S4 - S1 * C4) * S6; 58 double ny = ((S1 * S23 * C4 - C1 * S4) * C5 + S1 * C23 * S5) * C6 - (S1 * S23 * S4 + C1 * C4) * S6; 59 double nz = (C23 * C4 * C5 - S23 * S5) * C6 - C23 * S4 * S6; 66 return new double[] { nx, ny, nz }; 67 } 68 /// <summary> 69 /// 关节末端的空间姿态-o向量[ox,oy,oz] 70 /// </summary> 71 /// <param name="Ang">每个关节的角度值</param> 72 /// <returns>[ox,oy,oz]</returns> 73 public static double[] R6O(double[] Ang) 74 { 75 double C1 = Math.Cos(Ang[0]); 76 double S1 = Math.Sin(Ang[0]); 79 double C3 = Math.Cos(Ang[2]); 80 double S3 = Math.Sin(Ang[2]); 81 double S23 = Math.Sin(Ang[1] + Ang[2]); 82 double C23 = Math.Cos(Ang[1] + Ang[2]); 83 double C4 = Math.Cos(Ang[3]); 84 double S4 = Math.Sin(Ang[3]); 85 double C5 = Math.Cos(Ang[4]); 86 double S5 = Math.Sin(Ang[4]); 87 double C6 = Math.Cos(Ang[5]); 88 double S6 = Math.Sin(Ang[5]); 89 double ox = ((C1 * S23 * C4 + S1 * S4) * C5 + C1 * C23 * S5) * (-S6) - (C1 * S23 * S4 - S1 * C4) * C6; 90 double oy = ((S1 * S23 * C4 - C1 * S4) * C5 + S1 * C23 * S5) * (-S6) - (S1 * S23 * S4 + C1 * C4) * C6; 91 double oz = (C23 * C4 * C5 - S23 * S5) * (-S6) - C23 * S4 * C6; 97 return new double[] { ox, oy, oz }; 98 } 99 /// <summary> 100 /// 关节末端的空间姿态-a向量[ax,ay,az] 101 /// </summary> 102 /// <param name="Ang">每个关节的角度值</param> 103 /// <returns>[ax,ay,az]</returns> 104 public static double[] R6A(double[] Ang) 105 { 106 double C1 = Math.Cos(Ang[0]); 107 double S1 = Math.Sin(Ang[0]); 108 double C3 = Math.Cos(Ang[2]); 111 double S3 = Math.Sin(Ang[2]); 112 double S23 = Math.Sin(Ang[1] + Ang[2]); 113 double C23 = Math.Cos(Ang[1] + Ang[2]); 114 double C4 = Math.Cos(Ang[3]); 115 double S4 = Math.Sin(Ang[3]); 116 double C5 = Math.Cos(Ang[4]); 117 double S5 = Math.Sin(Ang[4]); 118 double C6 = Math.Cos(Ang[5]); 119 double S6 = Math.Sin(Ang[5]); 120 double ax = (C1 * S23 * C4 + S1 * S4) * (-S5) + C1 * C23 * C5; 121 double ay = (S1 * S23 * C4 - C1 * S4) * (-S5) + S1 * C23 * C5; 122 double az = C23 * C4 * (-S5) - S23 * C5; 128 return new double[] { ax, ay, az }; 129 }




