机器人末端的微分运动,可以通过雅可比矩阵(导数矩阵)投射到每个关节的角度上,即:
[D] = [J][Dθ]
[D]:末端的位置、转角微分矩阵;[J]:雅可比矩阵;[Dθ]为各关节的角度微分矩阵;如果两端除以时间微分(扫描周期),就可以由末端速度计算出关节角速度;对于三关节及以下的情况,[D]只需要三个位置微分就可以了,对于六关节机器人,[D]由三个位置微分与三个转角微分组成:[dx,dy,dz,δx,δy,δz],对于位置微分比较容易获得,但得到转角微分需要一定的计算。
绕x,y,z轴的旋转矩阵为:
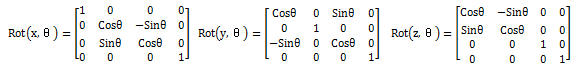
微分旋转矩阵由
θ==>0:
Sinθ==>θ;
Cosθ==>1;得到:

微分算子矩阵(忽略所有高阶微分):
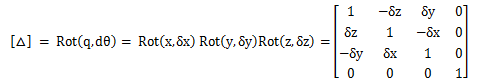
机器人的末端姿态表示为:

由:
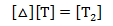
则微分算子:
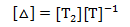
实际计算过程中,由于px,py,pz因坐标旋转导致位置移动,不但增加了计算量,而且计算出的位置微分有偏差,因此将位置部分取出:
dx = px2 - px;
dy = py2 – py;
dz = pz2 – pz;
这样就变成3x3的矩阵运算:
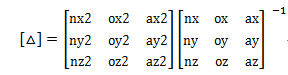
由于[n,o,a]互为垂直的单位向量:
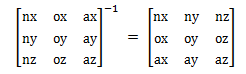

则:

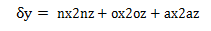
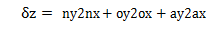
最后得到 [D] = [dx,dy,dz,δx, δy,δz]




