一、最小二乘法(Least Squares):
假设样本集单个样本的线性函数为:
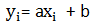
为解二元一次方程中的a,b,给上式两边乘以xi得到(也可以两边乘yi):
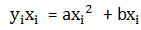
方程组:
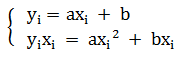
解样本集方程组:

矩阵形式:

对矩阵 求逆:
求逆:
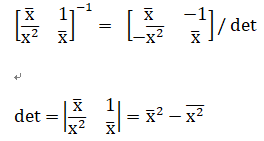
则:
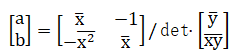
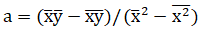


1 public static void LeastSquare(List<Point> points, out double a, out double b) 2 { 3 int N = points.Count; 4 if (N < 2) 5 { 6 a = 0; 7 b = 0; 8 return; 9 } 10 double X1 = 0, Y1 = 0, X2 = 0, X1Y1 = 0; 11 for (int i = 0; i < N; ++i) 12 { 13 X2 += points[i].X * points[i].X; 14 X1 += points[i].X; 15 X1Y1 += points[i].X * points[i].Y; 16 Y1 += points[i].Y; 17 } 18 a = (X1Y1 * N - X1 * Y1) / (X2 * N - X1 * X1); 19 b = (X2 * Y1 - X1 * X1Y1) / (X2 * N - X1 * X1); 20 }
二、梯度下降法(Gradient Descent):
针对离散数据样本集的最小化函数为:
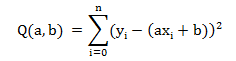
样本集中单一数据的Q函数对a、b偏导数:
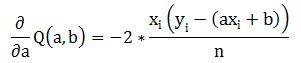
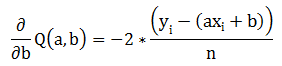
批样本集梯度:
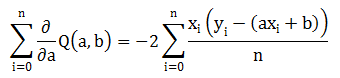
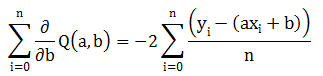

1 public static double[] Gradient_Descent(List<Point> points, double starting_a, double starting_b, double learningRate, int num_iterations) 2 { 3 double a = starting_a; 4 double b = starting_b; 5 int iter = 0; 6 while (iter < num_iterations) 7 { 8 double lasta = a; 9 double lastb = b; 10 double a_gradient = 0; 11 double b_gradient = 0; 12 int N = points.Count; 13 double x, y; 14 for (int i = 0; i < N; i++) 15 { 16 x = (double)points[i].X; 17 y = (double)points[i].Y; 18 19 a_gradient += -(2.00 / N) * x * (y - ((a * x) + b)); 20 b_gradient += -(2.00 / N) * (y - ((a * x) + b)); 21 } 22 a -= (learningRate * a_gradient); 23 b -= (learningRate * b_gradient); 24 if (Math.Abs(b- lastb) <0.00000001&& Math.Abs(a - lasta) < 0.00000001) 25 break; 26 iter++; 27 } 28 double totalError = 0; 29 for (int i = 0; i < points.Count; i++) 30 { 31 double x = (double)points[i].X; 32 double y = (double)points[i].Y; 33 totalError += Math.Pow((y - (a * x + b)), 2); 34 } 35 double error = totalError / points.Count; 36 37 return new double[] { a, b ,(double)iter,error}; 38 }





