【题解】P5049 [NOIP2018 提高组] 旅行 加强版（图论，dfs，基环树，贪心）
【题解】P5049 [NOIP2018 提高组] 旅行 加强版
是道好题！
但是我不知道它和 DP 究竟有什么关系。。毕竟我是看见 DP 的 tag 才点进来做的。
另外评紫可能……有一点点高。（毕竟连我这种蒟蒻都能想到。。）
题目链接
P5049 [NOIP2018 提高组] 旅行 加强版 - 洛谷
题意概述
有一张 \(n\) 个点 \(m\) 条边的无向图，其中 \(m=n-1\) 或 \(n\)，求一条路径，满足：
-
至少经过 \(1\) 到 \(n\) 中所有点一次；
-
每条边最多被访问两次；
-
在访问这一条路径的过程中，每次将新遍历到的节点加入到一个序列序列中，使得这条路径形成的序列在所有符合条件的路径中字典序最小。
思路分析
首先我们要学会观察数据范围。
（于是我这个傻逼因为没看数据范围挂了一下午。。）
可以发现，起点只可能是 \(1\)，因为只有从 \(1\) 开始所经过的路径字典序才可能满足最小，这是显然的。
由于 \(m\) 只可能是 \(n-1\) 或 \(n\)。那么我们可以直接分类讨论：
当 \(m=n-1\) 时：
显然这部分是一棵树，不可能”走回头路“，那么我们可以直接贪心的 dfs，每次选择一条边一直走到叶子节点然后返回走下一条边。假如当前走到了 \(x\)，那么直接选与 \(x\) 连边的所有未访问的点中，字典序最小的即可。
正确性证明：
当这是一棵普通的树时，显然对于每个点，从起点 \(1\) 开始有且仅有一条路径经过这个节点，也就是说这个节点只能通过这一条路径被访问到。
那么如果没有走到叶子节点就走”走回头路“，那么叶子节点就永远也不可能被访问到。因为当前边在”走回头路“之后就已经被访问了两次。
所以每次选择最小的儿子走即可。
当 \(m=n\) 时：
这就相当于是在一棵树上，连了一条边，也就是说，这张图中有且仅有一个环，我们将其称之为基环树。
显然我们不能再按照树上做法来做，原题样例 \(2\) 就是一个反例。
那么怎么办呢？
我们可以考虑，将整张图分为环上部分和非环上部分来做。
显然对于非环上部分，我们可以直接像树上一样 dfs。
对于环上部分，由于整张图有且仅有一个环，并且由于求字典序最小，所以进入环的起点是固定的，那么这个环上一定有且仅有一条边未被走过，可以暴力枚举哪一条边是未被走过的边，然后直接 dfs 即可。
这个复杂度最坏情况下是 \(O(n^2)\) 的。
这个时间复杂度已经可以过掉原题数据了，但无法过掉加强版。
考虑如何优化。
相比于树上普通的 dfs，我们实际上就是加了一个“走回头路”的”反悔“操作。
那么我们可以考虑这个操作何时进行。
首先，在环上 dfs 过程中，只有当之前访问过的并且在环上的节点，有一个未被访问的儿子的节点编号小于当前将要访问的节点时，才有可能进行“反悔”操作。
其次，在“反悔”之前，当前节点的所有非环上儿子已经被访问过。因为这些节点不再环上，无法通过除了这个节点之外的其它节点被访问到。
最后，在一整张图中，由于只有一个环，所以”反悔“操作最多只能进行一次。
以上是分析过程，接下来我们来梳理一下进行反悔操作的条件：
-
以前未“反悔”过；
-
当前节点的所有非环上儿子都已经被访问过；
-
之前访问过的并且在环上的节点，有一个未被访问的儿子的节点编号 \(p\) 小于当前将要访问的节点 \(q(p<q)\)。
具体实现的过程中，我们可以在 dfs 的过程中搞一个小根堆，对于一个节点 \(x\)，将其所有未被访问的儿子放入堆中，每次弹出最小的，然后判断是否满足“反悔”条件，若满足直接返回；反之则继续往下 dfs。
注意这里满足“反悔”条件时直接返回是可以的，因为总会返回到一个比它小的能访问的节点。
这一部分的代码如下：
void dfs2(int x,int fa,int now)//这里的 now 表示的是上一个已经被访问过的环上节点的未被访问过的儿子。
{
priority_queue<int>q;
cout<<x<<" ";
vis[x]++;
for(int y:edge[x])
{
if(y==fa||vis[y])continue;
q.push(-y);//负值入队是大根堆转小根堆。
}
while(!q.empty())
{
int tt=-q.top();
q.pop();
if(!flag&&t[tt]&&q.empty()&&now<tt){flag=true;return ;}
//flag 表示是否进行过“反悔”操作，t[] 存储的是节点是否在环上。
if(!vis[tt])//若该节点当前仍然未被访问过则从该节点向下 dfs。
{
int kk=-q.top();
if(!q.empty()&&t[x])dfs2(tt,x,kk);//如果 x 在环上并且还有其它儿子未被访问，则说明可以回溯到 x。
else dfs2(tt,x,now);
}
}
}
除此之外，由于我们要分为环上和非环上两部分，所以我们还需要一个基环树上找环的操作。
我们可以从起点开始 dfs，然后每次访问到一个新的节点就将其标记为访问过。一旦访问到之前访问过的节点，就说明该节点在环上，那么直接回溯，在回溯到环上起点的过程中，把途中访问过的所有节点标记为环上节点即可。
这部分可能有点抽象，我们来看一张图：
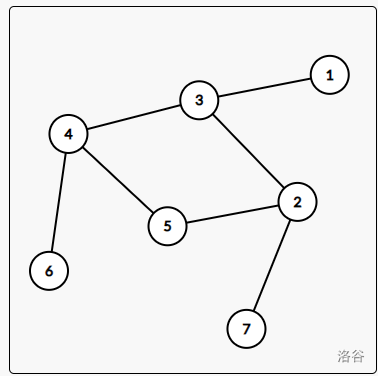
这张图上的环是：\(3-2-5-4\)。
我们找环的过程如下：
从起点 \(1\) 出发，vis[1]++；
分别访问 \(3-2-5-4\)，并将它们的 vis 加一；
然后访问 \(3\)，此时由于 vis[3]!=0，所以标记 \(3\) 在环上：t[3]++；
然后回溯，回溯的过程中经过 \(2-5-4\)，并将它们标记在环上；
最后回到 \(3\)，发现 \(3\) 本身在环上，说明找到了环，dfs 结束。
有人可能会问：那 \(6\) 和 \(7\) 是干嘛的？难道遍历不到它们吗？
答：可能会被遍历到，但无论是否遍历它们，对找环并没有影响。
因为是否遍历它们取决于加边的顺序，比如在这张图中，若 \(2-5\) 在 \(2-7\) 之后加边，那么就会先遍历到 \(7\)，但遍历到 \(7\) 之后发现 \(7\) 不在环上会很快回溯。所以遍历它并不影响找环的过程。
基环树上找环到这里就结束了。
这部分代码如下：
void dfs(int x,int fa)
{
vis[x]++;
for(int y:edge[x])
{
if(y==fa)continue;
if(vis[y])
{
t[y]++;
flag=true;//flag 表示当前是否在环上。
return ;
}
dfs(y,x);
if(flag==true)
{
if(t[x])flag=false;//说明回到起点，将 flag 重新标记为 false。
else t[x]++;
return ;
}
}
}
时间复杂度：\(O(n \log n)\)。
关键点
-
想到最多会“反悔”一次；
-
基环树上找环；
-
弄清楚“反悔”条件。
代码实现
//luogu5022
#include<cstdio>
#include<iostream>
#include<cstring>
#include<string>
#include<queue>
#include<algorithm>
#define int long long
using namespace std;
const int maxn=5e5+10;
const int INF=0x3f3f3f3f;
int vis[maxn],t[maxn];
bool flag;
basic_string<int>edge[maxn];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void dfs(int x,int fa)
{
vis[x]++;
for(int y:edge[x])
{
if(y==fa)continue;
if(vis[y])
{
t[y]++;
// t[x]++;
flag=true;
return ;
}
dfs(y,x);
if(flag==true)
{
if(t[x])flag=false;
else t[x]++;
return ;
}
}
}
void dfs2(int x,int fa,int now)
{
priority_queue<int>q;
cout<<x<<" ";
vis[x]++;
for(int y:edge[x])
{
if(y==fa||vis[y])continue;
// cout<<"ex "<<x<<" "<<y<<endl;
q.push(-y);
}
while(!q.empty())
{
int tt=-q.top();
q.pop();
// cout<<x<<" "<<tt<<endl;
// cout<<flag<<" "<<t[tt]<<" "<<now<<endl;
if(!flag&&t[tt]&&q.empty()&&now<tt){flag=true;return ;}
if(!vis[tt])
{
int kk=-q.top();
if(!q.empty()&&t[x])dfs2(tt,x,kk);
else dfs2(tt,x,now);
}
// cout<<"---------------"<<endl;
}
}
signed main()
{
int n,m;
n=read();m=read();
for(int i=1;i<=m;i++)
{
int u,v;
u=read();v=read();
edge[u]+=v;edge[v]+=u;
}
// for(int i=1;i<=n;i++)
// {
// sort(edge[i].begin(),edge[i].end());
// }
vis[1]++;
dfs(1,0);
memset(vis,0,sizeof(vis));
flag=false;
dfs2(1,0,INF);
return 0;
}
