【题解】P3600 随机数生成器(概率,期望)
【题解】P3600 随机数生成器
期望好题!
这道题从 11 号下午开始在机房写的,从十一号晚上调到十三号凌晨,终于调过去了!
第四道黑!(激动)
这道题让我自己是无论如何都想不出来的。这里完整详细叙述一遍思路,帮我自己梳理一遍。
更新日志:
upd on 2022.5.17:增加了易错点部分详解和加入了少量代码注释。
题目链接
思路分析
从问题入手,问题是求这 \(q\) 个区间中每个区间最小值的最大值的期望。
根据期望的定义,那么有:
其中 \(f_i\) 表示的是区间最大值恰好为 \(i\) 的方案数。
考虑对于每个区间来说,显然若这个区间 \(A\) 包含另一个区间 \(B\),那么这个区间 \(A\) 的最小值一定小于等于区间 \(B\)。
由于我们要求的是区间最小值的最大值,那么可以看出,区间 \(A\) 对最后答案无影响。
那么我们就可以把这些区间 \(A\) 删掉。可以发现,如果把剩下的区间按左端点从小到大排序,那么右端点一定是严格单调递增的。
回到上面那个式子。
显然 \(x^n\) 可以直接快速幂求得,那么问题就转化为如何求 \(f_i\)。
\(f_i\) 并不好求,根据常用套路,那么我们可以考虑将恰好转化为最多。
定义 \(g_i\) 表示的是区间最大值 \(\le i\) 的方案数。
那么对于每一个 \(i\),利用类似前缀和差分的思想,有:
即:区间最大值恰好为 \(i\) 的方案数是区间最大值 \(\le i\) 的方案数减去区间最大值 \(\le i-1\) 的方案数。
考虑如何求 \(g_i\)。
当区间最大值整体 \(\le i\),那么就说明:每个区间都至少有一个 \(\le i\) 的数。
那么有:
\(tp_j\) 表示的是在 \(1-n\) 个区间里的所有数中,选出 \(j\) 个 \(\le i\) 的点,每个区间至少包含一个点的方案数。
我们要计算 \(g_i\),可以枚举 \(j\),那么对于这 \(j\) 个 \(\le i\) 的点,有 \(i^j\) 种情况;对于剩下 \(> i\) 的 \(n-j\) 个点,有 \((x-i)^{n-j}\) 种情况;那么根据乘法原理,每个 \(j\)对 \(g_i\) 的贡献就是:
最后累加求和即可。
现在问题转化成如何求 \(tp_i\)。
考虑 DP。
定义 \(dp_{i,j}\) 表示的是前 \(i\) 个位置放了 \(j\) 个点,且第 \(i\) 个位置必须放点,覆盖所有的左端点 \(\le i\) 的区间的方案数。
我们定义 \(L_i\) 和 \(R_i\) 分别表示覆盖位置 \(i\) 的最左和最右区间编号。
特殊地,对于没有被任何区间覆盖的位置 \(i\),\(R_i\) 定义为右端点严格小于 \(i\) 的最后一个区间,\(L_i=R_i+1\)。
那么有:
枚举 \(i,j,k\),时间复杂度 \(O(n^3)\)。
考虑优化。可以发现参与转移的 \(k\) 是一段连续的区间,那么前缀和优化即可。时间复杂度:\(O(n^2)\)。
即:
其中 \(sum_{i,j}\) 表示的是上一层的 \(\sum \limits_{k=1}^i dp_{k,j}\)。
这里要注意的一点是:\(k-1\) 有可能为负,所以要特判 \(k=0\) 的情况。(我因为这个问题挂了一下午,而且本地测试挂了点还能过就很离谱)
那么 \(g_j\) 就可以计算出:
总的时间复杂度:\(O(n^2)\)。
最后我们来梳理一下求解过程:
求期望 \(\rightarrow\) 求区间最大值恰好为 \(i\) 方案数 \(f_i \rightarrow\) 求区间最大值 \(\le i\) 的方案数 \(g_i \rightarrow\) 求每个区间都至少有一个 \(\le i\) 的点的方案数 \(tp_i \rightarrow\) 求 \(dp_{i,j}\)。
求解步骤
-
区间去重+排序:暴力枚举;
-
求出每个点 \(i\) 的 \(R_i,L_i\):对于区间 \([1,x]\) 的每个点,暴力枚举每个区间计算,最后特判在最后一个区间右边的点;
-
枚举 \(i,j\),前缀和优化,计算出 \(dp_{i,j}\);
-
枚举 \(j\),根据 \(dp_{i,j}\),计算出 \(tp_j\);
-
枚举 \(i\),根据 \(tp_j\) 计算 \(g_i\);
-
根据 \(g_i\) 计算出 \(f_i\);
-
套用公式 \(\frac {\sum \limits_{i=1}^x f_i\times i}{x^n}\) 计算出最终答案。
易错点
这题调了不知道多久……提交了 15 次。。。
-
关于区间去重+排序:
-
暴力枚举两个区间 \(i,j\) 是否包含时,要注意 \(i \ne j\);
-
当两个区间左右端点相同并且其中一个端点已经被标记为删除点时,不需要去重,即:
if(a[i].l==a[j].l&&a[i].r==a[j].r&&(vis[i]||vis[j])) continue;;
-
-
关于求 \(R_i,L_i\):
这里由于有很多不同的处理方法,所以先放出我的处理方法:
void work()//求出 L[i] 和 R[i] { for(int i=1;i<=x;i++) { int j; for(j=1;j<=q;j++) { if(b[j].l<=i&&b[j].r>=i) { if(!L[i])L[i]=j; R[i]=j; } else if(b[j].l>i) { if(!L[i])R[i]=j-1,L[i]=R[i]+1; //若 i 不被任何区间所覆盖,则 R[i] 设为最后一个右端点比它小的区间编号,L[i]=R[i]+1; break; } } if(!L[i])R[i]=R[i-1],L[i]=R[i]+1; } }我枚举 \(1-x\) 的每个点作为 \(i\),求出 \(L_i,R_i\)。
最易错的点就是,当一个点没有被任何区间覆盖时,有两种情况:
一是在两个区间之间的“空隙”里,即:
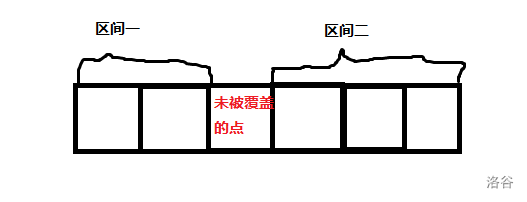
这种情况下,我们只需要在循环时特判一下:遇到一个左边界已经大于它的点 \(j\),那么 \(R_i=j-1,L_i=R_i+1\)。
二是在最后一个区间后面,即:
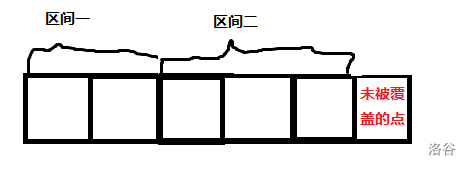
这时不能仿照上面的处理方式了,我们需要在循环结束时判断一下这个点是否为最右端区间后面的点,具体做法就是判断 \(L_i\) 是否为 0(是否被更新过),若为 0,则说明这个点就是最右端区间后面的点,那么:
R[i]=R[i-1],L[i]=R[i]+1;,这里要注意的一点是,这里的 \(R_i\) 赋值为 \(R_{i-1}\)。我在这挂了至少半个小时。 -
计算 \(dp_{i,j}\):
因为 \(dp_{i,j}=\sum \limits_{R_k+1 \ge L_i}dp_{k,j}\),我们要使用前缀和优化就必须找到最小的 \(k\)。
所以我们通过
while(k<i-1&&R[k]+1<L[i])k++;来找到 \(k\)。那么有一种可能 \(k=0\),那么在计算 \(sum_{k-1,j-1}\) 就会访问到负下标,会 RE(但是不知道为啥我的代码一直是 WA 并且本地编译毫无错误),所以需要特判一下,即:dp[i][j]=(sum[i-1][j-1]-(k?sum[k-1][j-1]:0)+mod)%mod; -
还是一样的套路,取模运算不要忘掉 ( +mod)%mod;
-
整个 DP 部分用到很多 for 语句不要把边界弄混了(分清楚 \(x,n\),不要写反 \(i,j,k\))
实现代码
//luoguP3600
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<stack>
#define int long long
using namespace std;
const int mod=666623333;
const int maxn=2005;
struct Node{int l,r;}a[maxn],b[maxn];
int n,x,q;
int cnt,mx,ans,mi;
int vis[maxn],book[maxn],L[maxn],R[maxn];
//L[i] 和 R[i] 分别表示 i 可以覆盖到的编号最小和最大的区间
int dp[maxn][maxn],tp[maxn],g[maxn],f[maxn],sum[maxn][maxn];
//dp[i][j] 表示前 i 个位置放了 j 个√,且第 i 个位置必须放√,覆盖所有的左端点 <=i 的区间的方案书。
//tp[i] 表示的是在 [1,n] 内选出 i 个点,每个区间至少包含一个点的方案数。
//g[i] 表示的是区间最大值 <=i 时的方案数。
//f[i] 表示区间最大值恰好 =i 时的方案数。
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int cmp(Node a,Node b){if(a.l==b.l)return a.r<b.r;return a.l<b.l;}
void init()//去重(将包含区间去除)
{
for(int i=1;i<=q;i++)
{
for(int j=1;j<=q;j++)
{
if(i==j)continue;//注意 i 不能等于 j。
if(a[i].l==a[j].l&&a[i].r==a[j].r&&(vis[i]||vis[j])) continue;
if(a[i].l>=a[j].l&&a[i].r<=a[j].r)vis[j]++;
else if(a[i].l<=a[j].l&&a[i].r>=a[j].r)vis[i]++;
}
}
for(int i=1;i<=q;i++)
{
if(!vis[i])b[++cnt].l=a[i].l,b[cnt].r=a[i].r;
}
return ;
}
void work()//求出 L[i] 和 R[i]
{
//cout<<mx<<endl;
for(int i=1;i<=x;i++)
{
int j;
for(j=1;j<=q;j++)
{
if(b[j].l<=i&&b[j].r>=i)
{
if(!L[i])L[i]=j;
R[i]=j;
}
else if(b[j].l>i)
{
if(!L[i])R[i]=j-1,L[i]=R[i]+1;
//若 i 不被任何区间所覆盖,则 R[i] 设为最后一个右端点比它小的区间编号,L[i]=R[i]+1;
break;
}
}
if(!L[i])R[i]=R[i-1],L[i]=R[i]+1;//处理在最后一个区间后面的点的情况
}
}
int qpow(int a,int T)
{
int ret=1;
while(T)
{
if(T&1)(ret*=a)%=mod;
(a*=a)%=mod;T>>=1;
}
return ret;
}
void out()
{
for(int i=1;i<=x;i++)cout<<L[i]<<" "<<R[i]<<endl;
/*for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)cout<<dp[i][j]<<endl;
}*/
//for(int i=1;i<=n;i++)cout<<tp[i]<<endl;
}
void DP()
{
//求 dp[i][j]
dp[0][0]=sum[0][0]=1;
int k=0;
for(int i=1;i<=n;i++)
{
while(k<i-1&&R[k]+1<L[i])k++;
for(int j=1;j<=i;j++)
{
dp[i][j]=(sum[i-1][j-1]-(k?sum[k-1][j-1]:0)+mod)%mod;//防止负下标
}
for(int j=0;j<=i;j++)sum[i][j]=(sum[i-1][j]+dp[i][j])%mod;
}
//out();
//求 tp[j]
for(int i=1;i<=n;i++)
{
if(R[i]!=cnt)continue;//注意这里是 R[i]!=cnt 而非 R[i]!=n
for(int j=1;j<=n;j++)
{
(tp[j]+=dp[i][j])%=mod;
}
}
//out();
//求 g[i]
for(int i=1;i<=x;i++)
{
for(int j=1;j<=n;j++)
{
(g[i]+=tp[j]*qpow(i,j)%mod*qpow(x-i,n-j)%mod)%=mod;
}
}
//out();
//求 f[i]
for(int i=1;i<=x;i++)f[i]=(g[i]-g[i-1]+mod)%mod;
//out();
int e=qpow(qpow(x,n),mod-2);//最后答案要除以 x^n
for(int i=1;i<=x;i++)(ans+=(i*f[i]%mod*e%mod))%=mod;
}
signed main()
{
n=read();x=read();q=read();
for(int i=1;i<=q;i++)
{
a[i].l=read();a[i].r=read();
}
sort(a+1,a+q+1,cmp);
init();
sort(b+1,b+cnt+1,cmp);//按 l 排序,保证 r 严格递增。
work();
DP();
cout<<ans<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号