【题解】P3225 [HNOI2012]矿场搭建（割点，dfs）
【题解】P3225 [HNOI2012]矿场搭建
割点好题！
（因为刚开始没想清楚卡了好久/kk）
题目链接
题意概述
给定一张 \(n\) 条边的无向图，现在要求在其中一些点上修建一些“出口”，使得断掉任意一个点之后，都能使得其它点可以到达至少一个“出口”。问最少要设置多少个出口，以及方案数是多少。
思路分析
这个其实很容易看出来要用割点。关键是怎么用。
首先由于这道题中没有告诉点的个数，我们假设点的个数为 \(m\)，并将断掉所有割点后的图视为一个个连通块。
我们可以考虑根据图中割点个数进行分类讨论：
-
当图中没有割点时，也就是图是一张点双连通图时。
如果设置一个“出口”，那么对其它点无所谓，但若设置了出口的点断掉，那么其它点就不能到达任意一个出口，所以只能至少设置两个点。
在点双中，每个点都是等价的。所以可以在 \(m\) 个点中任选两个作为“出口”，即方案数为 \(\mathrm C_m^2=\frac {m \times (m-1)}{2}\)。
-
当图中有割点时：
-
假如断的是割点：那么与这个割点相连的连通块中的点，要么这个连通块中本身有“出口”，要么这个连通块的点可以通过另一个与之相连的割点到达另一个连通块中，而到达的那个连通块中有“出口”。但对于只与一个割点相连的连通块，我们只能通过第一种方式到达“出口”，我们称这样的连通块为叶子连通块。
那么每一个叶子连通块中内部必须有一个“出口”，否则无法满足题意。那么当所有叶子连通块中都有一个出口时，对于非叶子连通块，那么就一定有一条路径使得这个连通块的节点能够到达其中一个叶子连通块，所以就不必在这些非叶子连通块中再设立“出口”。
这里可能有点抽象，我们画个图理解一下：
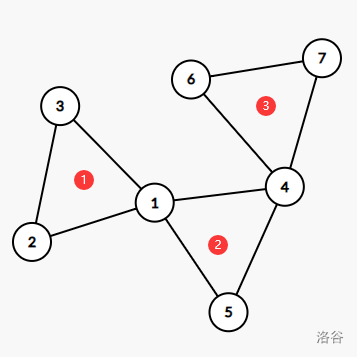
如图，在这张图中，点 \(1,2,3\) 构成 ① 号的连通块和 \(4,6,7\) 构成的 ③ 号连通块都分别只与割点 \(1\) 和割点 \(4\) 相连，都是叶子连通块。而由于点 \(1,4,5\) 构成的 ② 号连通块与 \(1,4\) 两个割点相连，所以它不是叶子连通块。
那么假如当 \(1\) 或 \(4\) 断开时，①/③ 号连通块的点都不能通过其它方式到达 ② 号连通块，所以必须要在它们两个连通块内部设置两个“出口”。
而对于 ② 号连通块，不管是断了 \(1\) 还是断了 \(4\)，它都可以通过另一个割点到达另一个连通块中，所以无需在这个连通块中设置“出口”。
所以这种情况下，就直接在每一个叶子连通块中设立一个出口就好了。
那么答案就为整张图中叶子连通块的个数，根据乘法原理，方案数就为每个叶子联通块的大小乘积。
-
假如断开的不是割点：那么对于任意一个连通块中的点，都可以通过割点到达另一个连通块中去，也就是说，我们只需要设置一个“出口”即可。
综上，当图中有割点时，我们可以只考虑在叶子连通块中设置“出口”。
那么现在问题就转化为，如何求出图中有多少个叶子连通块，以及每个叶子连通块的大小是多少。
比较好想的一种思路是：
首先第一遍 dfs 找出所有割点并把它们标记出来。
第二遍枚举所有的点，如果这个点不是割点并且没有被访问过则从这个点开始 dfs。
dfs 的过程中将走过的所有点标记为已访问，假设当前遍历到的点是 \(x\)，那么遍历到 \(x\) 时首先 \(vis_x++\)，然后对于与 \(x\) 连边的所有点 \(y\)，当且仅当 \(y\) 没有被访问过且 \(y\) 不是割点时继续 dfs \(y\) 这个点。
除此之外，我们还要判断当前连通块是否为叶子连通块。
根据叶子连通块的定义，我们可以考虑在 dfs 的过程中维护当前连通块与几个割点相连。我们用一个 \(book\) 数组来表示每个割点是否被 dfs 到过，对于割点 \(t\)，若 dfs 到过则 \(book=1\)，反之则为 \(0\)。并用一个变量 \(num\) 表示有多少个割点与当前连通块相连。
延续上面的 \(x\)，当我们在遍历到与 \(x\) 连边的所有 \(y\) 时，如果 \(y\) 是割点且 \(book_y=0\) 则 \(num++\) 并将 \(book_y\) 标记为 \(1\)。
这样对于遍历到的每个连通块，若 dfs 结束后 \(num=1\) 则说明它是叶子连通块。
那么如何求出每个连通块的大小呢？
我们可以考虑维护一个数组 \(sz_x\) 表示以 \(x\) 为根的子树大小。
那么我们在枚举所有点求叶子连通块时，假如枚举到一个符合要求点 \(x\) 开始 dfs，最后的答案 \(sz_x\) 就是 \(x\) 所在连通块的大小。
现在问题就转化为如何求出 \(sz_x\)，其实这很简单：
\[ sz_x= \sum \limits_{x 与 y 连边且 y\ne fa_x} sz_y \]直接维护即可。具体详见代码。
易错点
- 本题中有多个变量和数组，且数据多测，请不要忘了清空数组。
- 我一开始一直有一个错误的思路就是对于有割点的情况，答案是连通块个数，并没有考虑到对于一个非叶子连通块来说，其中一个割点断了还可以通过另一个割点“逃出去”。所以要仔细思考，注意题目的关键条件。
代码实现
//luoguP3225 //10:41 #include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #define pii pair<int,int> #define mk make_pair #define int long long #define debug using namespace std; const int maxn=1005; int dfn[maxn],low[maxn],sz[maxn],ok[maxn],cnt,tot,rt,num,now; int vis[maxn],book[maxn][maxn]; basic_string<pii>edge[maxn]; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();} return x*f; } void dfs(int x,int pre) { dfn[x]=low[x]=++tot; int ret=0; for(auto nxt:edge[x]) { int y=nxt.first,id=nxt.second; if(!dfn[y]) { dfs(y,id); low[x]=min(low[x],low[y]); if(low[y]>=dfn[x])ret++; } else if(id!=pre)low[x]=min(low[x],dfn[y]); } if(ret>=2||(ret==1&&pre!=0))ok[x]++,rt++; return ; } void dfs2(int x,int fa) { #ifdef debug2 cout<<x<<" "<<fa<<endl; #endif sz[x]=1; vis[x]++; for(auto nxt:edge[x]) { int y=nxt.first; if(y==fa||vis[y])continue; if(ok[y]) { if(book[now][y]==0){num++;book[now][y]++;} continue; } dfs2(y,x); sz[x]+=sz[y]; } } signed main() { int T=0; int n=read(); while(n) { #ifdef debug2 cout<<"n="<<n<<endl; #endif T++; cout<<"Case "<<T<<": "; for(int i=1;i<=n;i++)edge[i].clear(); memset(dfn,0,sizeof(dfn)); memset(low,0,sizeof(low)); memset(vis,0,sizeof(vis)); memset(ok,0,sizeof(ok)); memset(sz,0,sizeof(sz)); cnt=0;tot=0;rt=0; int mx=0; for(int i=1;i<=n;i++) { int u,v; u=read();v=read(); edge[u]+=mk(v,i); edge[v]+=mk(u,i); mx=max({mx,u,v}); } for(int i=1;i<=mx;i++)if(!dfn[i])dfs(i,0); if(rt==0) { cout<<2<<" "; cout<<mx*(mx-1)/2<<'\n'; n=read(); continue; } // cout<<cnt+1<<" "; int ans=1; #ifdef debug2 cout<<cnt<<endl; #endif for(int i=1;i<=mx;i++) { #ifdef debug2 cout<<i<<" "<<ok[i]<<"\n"; #endif if(ok[i])continue; if(!vis[i]) { num=0;now=i; dfs2(i,0); #ifdef debug2 cout<<"i="<<i<<" "<<num<<'\n'; #endif if(num>1)continue; ans*=sz[i]; cnt++; } } cout<<cnt<<" "<<ans<<'\n'; n=read(); } return 0; } /* 分类讨论一下： - 当图中没有割点时：答案为 2，方案数为 v*(v-1)/2。 - 当图中有割点时，答案就是删掉割点后的连通块数量，方案数为每个"叶子"连通块的 sz 相乘。 */ -
