【题解】P3047 [USACO12FEB]Nearby Cows G(树形 DP,换根 DP)
【题解】P3047 [USACO12FEB]Nearby Cows G
可能是我做的最成功的题之一(?)
这道题对我意义挺大的。其实换根 DP 都好久没写过了,甚至其实第一次学这东西的时候就没学懂,今天看到这道题不到十分钟就反应过来这是个换根 DP,连我自己都挺惊讶,对一个完全不熟的知识点不到十分钟就能在题中发现它。
在复习了换根 DP 之后,写代码+想思路一气呵成,甚至没有任何调试一遍过样例+AC。突然就觉得,,我的付出不是没有回报,做了那么多题应该还是有很大进步的。
还是要坚信,我们的努力终有回报,付出终会有结果吧。
题目链接
P3047 [USACO12FEB]Nearby Cows G
题意概述
给你一棵 \(n\) 个点的树,点带权,对于每个节点求出距离它不超过 \(k\) 的所有节点权值和 \(m_i\)。
数据范围
对于 \(100\%\) 的数据:\(1 \le n \le 10^5,1 \le k \le 20,0 \le c_i \le 1000\)
思路分析
我们首先考虑对于一个点而言,它的答案由哪几部分构成:
- 它的子树所包含的所有距离它小于等于 \(k\) 的节点点权和;
- 除了它的子树之外的其它节点中距离它小于等于 \(k\) 的节点点权之和。
我们发现对于一个节点子树内小于等于 \(k\) 的节点点权和很容易求得(可以直接树形 DP),而子树外距离它小于等于 \(k\) 的点权和不易求得。
那么我们能否考虑把所有子树外的点也转化到子树内呢?
这就很自然的想到换根 DP。
暴力换根的思路是让每个节点都当一次根,然后算出以它为根时整棵树的答案。
这需要 \(n\) 次 dfs,时间复杂度是 \(O(n^2)\)。
而换根 DP,就只需要两次 dfs。将时间优化到了 \(O(n)\) 这个级别。
第一次 dfs 求出以 \(1\) 为根的答案。第二次 dfs 是将当前节点 \(u\) 为根切换到它的每一个儿子 \(v\) 为根,同时通过已经计算过的数据(递推式或者是直接的数)在 \(O(1)\) 这个级别的复杂度内就从 \(u\) 为根的结果得到 \(v\) 为根的结果。
简单来说,换根 DP 又称二次扫描,第一次 dfs 求 \(1\) 为根时的答案,第二次完成根节点切换求出所有点为根时的答案。
具体可详见:P3478 [POI2008] STA-Station
对于这道题,我们可以定义 \(dp_{x,i}\) 表示以 \(x\) 为根的子树内距离它为 \(i\) 的点权和。
这里可以直接树形 DP,比较简单,如下:
void dfs(int x,int fa)
{
dp[x][0]=a[x];
for(int y:edge[x])
{
if(y==fa)continue;
dfs(y,x);
for(int i=k;i>=1;i--)
{
dp[x][i]+=dp[y][i-1];
}
}
}
\(dp_{x,i}\) 就是对于它所有的儿子 \(y\) 来说 \(dp_{y,i-1}\) 之和,因为 \(x\) 到 \(y\) 还有 \(1\) 的距离。
需要注意的细节是 \(dp_{x,0}\) 要初始化为 \(x\) 的点权,因为距离 \(x\) 为 \(0\) 的点只有它自己嘛。
然后我们根据 \(dp\) 数组处理出来一个 \(sum_{x,i}\) 表示的是以 \(x\) 为根的子树内,距离 \(x\) 小于等于 \(i\) 的点权和。
很显然其实 \(sum\) 就是 \(dp\) 数组的前缀和,即 \(sum_{x,i}=\sum \limits_{j=1}^i dp_{x,j}\)。
接下来我们定义 \(tp_{x}\) 表示整棵树上距离 \(x\) 小于等于 \(k\) 的点权和,也就是最终的答案。
这个 \(tp_x\) 可以在第二次 dfs 中来求。
首先初始化 \(tp_1=sum_{1,k}\)。这是显然的。
我们考虑当根从 \(x\) 切换到它的儿子 \(y\) 时,\(tp_y\) 相较于 \(tp_x\) 有什么变化。
以图为例:
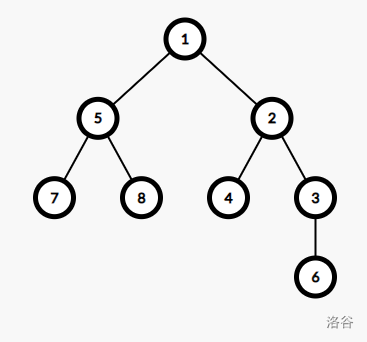
对于此图看,当 \(k=2\) 时,\(1\) 的答案是 \(5,7,8,1,2,4,3\) 这些点的点权之和,而 \(2\) 的答案是 \(5,1,2,4,3,6\) 这些点之和。
我们发现,实际上 \(2\) 的答案只比 \(1\) 的答案少了 \(7,8\) 这一层,多了 \(6\) 这一层。
一般地,当根从 \(u\) 变成 \(u\) 的儿子 \(v\) 时,答案少了除 \(v\) 极其子树外与 \(u\) 距离为 \(k\) 的点,多了 \(v\) 极其子树内与 \(v\) 距离为 \(k\) 的点。
那么我们定义 \(dd_{x,i}\) 表示整棵树中距离 \(x\) 为 \(i\) 的点权和。
注意:这里的 \(dd_{x,i}\) 与 \(dp_{x,i}\) 的含义不同,\(dp_{x,i}\) 的对象是以 \(1\) 为根 \(x\) 的子树,\(dd_{x,i}\) 是整棵树。
那么有:
我这个式子里的 \(dp_{v,k-1}\) 事实上就表示的是 \(v\) 子树内与 \(u\) 距离为 \(k\) 的点,因为与 \(u\) 距离为 \(k\),那么与 \(v\) 距离就变成了 \(k-1\)。
现在我们来看一下还有什么东西没有求出来,可以发现只有 \(dd\) 数组还不知道。
那么问题就转化为如何求 \(dd_{x,i}\)。
可以发现整棵树中距离 \(x\) 为 \(i\) 的点其实就等于以 \(1\) 为根时 \(x\) 子树内距离 \(x\) 为 \(i\) 的点+以 \(1\) 为根时 \(x\) 子树外距离 \(x\) 为 \(i\) 的点。
第一项就是 \(dp_{x,i}\),而第二项其实就是除 \(x\) 子树内距离 \(x\) 的父亲为 \(i-1\) 的点,即 \(dd_{fa[x],i-1}-dd_{x,i-2}\)。
这样就很容易了。我们只要第二次 dfs 每次顺便求一下 \(dd_{x,i}\) 就好了。
具体代码如下:
void dfs2(int x,int fa)
{
for(int y:edge[x])
{
if(y==fa)continue;
tp[y]=tp[x]-dp[x][k]+dp[y][k-1]+dp[y][k];
for(int i=k;i>=1;i--)
{
dp[y][i]+=dp[x][i-1];
if(i>=2)dp[y][i]-=dp[y][i-2];
}
dfs2(y,x);
}
}
需要说明一下,我这份代码里面并没有新定义一个数组 \(dd\),而是直接在 \(dp\) 数组上更新了,所以前后的 \(dp\) 数组含义不同。
如果觉得很乱想更清晰的话还是建议重新定义一个数组来求。
最后输出所有的 \(tp_i\) 即可。
关键点
- 想到换根 DP;
- 想清楚根交换时答案的变化。
代码实现
//luoguP3047
#include<cstdio>
#include<iostream>
#include<cstring>
#define debug
using namespace std;
const int maxn=1e5+10;
const int maxk=25;
int dp[maxn][maxk],dep[maxn],tp[maxn],a[maxn];
int sum[maxn][maxk];
int n,k;
basic_string<int>edge[maxn];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void dfs(int x,int fa)
{
dep[x]=dep[fa]+1;
dp[x][0]=a[x];
for(int y:edge[x])
{
if(y==fa)continue;
dfs(y,x);
for(int i=k;i>=1;i--)
{
dp[x][i]+=dp[y][i-1];
}
}
}
void dfs2(int x,int fa)
{
for(int y:edge[x])
{
if(y==fa)continue;
tp[y]=tp[x]-dp[x][k]+dp[y][k-1]+dp[y][k];
for(int i=k;i>=1;i--)
{
dp[y][i]+=dp[x][i-1];
if(i>=2)dp[y][i]-=dp[y][i-2];
}
dfs2(y,x);
}
}
int main()
{
n=read();k=read();
for(int i=1;i<n;i++)
{
int u,v;
u=read();v=read();
edge[u]+=v;
edge[v]+=u;
}
for(int i=1;i<=n;i++)a[i]=read();
dfs(1,0);
for(int i=1;i<=n;i++)
{
for(int j=0;j<=k;j++)
{
sum[i][j]=sum[i][j-1]+dp[i][j];
}
}
tp[1]=sum[1][k];
dfs2(1,0);
for(int i=1;i<=n;i++)cout<<tp[i]<<'\n';
return 0;
}
不管怎么说这题也算是我完整独立而且较为顺利自己 AC 的一道蓝题了。翻了翻题解区不管是说换根还是两遍 dfs 什么的,似乎都没有我题解详细(???),而我也只是写了一篇我自己觉得最佳的能理解的题解而已。
嗯……慢慢进步吧!
感谢阅读!


