【题解】P1979 [NOIP2013 提高组] 华容道（SPFA，BFS，常数优化）

【题解】P1979 [NOIP2013 提高组] 华容道

最近打比赛次次挂。。平均每周得被至少一场比赛打击一次（这周好不容易 ABC 打的还行模拟赛又挂……）心烦意乱。写篇题解疏散一下内心的苦闷（雾）。。。

这题正解是 SPFA+BFS，但是我直接 BFS 搜过了……

~~我才不会告诉你我提交了五十多遍卡常从 70 分卡 AC 了……~~

这是一篇玄学卡常题解（雾）。

题目链接

P1979 [NOIP2013 提高组] 华容道 - 洛谷

题意概述

有一个 \(n \times m\) 的棋盘，棋盘上的每个格子要么是空格要么是棋子，满足以下三种情况：

每个棋盘只有一个空格；
有些棋子可移动，有些棋子不可移动。
每个空格任何与空白的格子相邻（有公共的边）的格子上的棋子都可以移动到空白格子上。

题目要求把某个指定位置可以活动的棋子移动到目标位置。

给定空格格子的坐标，所有不可移动棋子（方便起见以下均简称为“障碍”）的坐标，以及需要移动的棋子的初始坐标和目标位置坐标，求最少需要几步；无解输出 -1。

题目分析

以下均为我当时这道题完整的思考过程。

第一眼看到这道题，我的第一直觉是 BFS。将空格作为起点，每次分别与相邻可交换的格子交换，并将每次交换后的结果插入队列中，直到需要移动的棋子移动到目标位置为止。

要注意的一点是，我们在一般的题目中的 BFS，判断一个状态是否走过采用的是利用一个二维数组 \(vis_{x,y}\) 标记，但这里由于不仅要表示空格在哪，还要表示要移动的棋子现在移动到了哪，所以我们用 \(vis_{x,y,nx,ny}\) 表示棋子现在移动到了 \((x,y)\) 并且当前空格在 \((nx,ny)\) 这个状态是否访问过。然后就可以愉快的 BFS 了。

于是就有了下面的代码（相信不用我多说）：

const int maxn=35;
int a[maxn][maxn],dis[maxn],vis[maxn][maxn][maxn][maxn];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int ex,ey,sx,sy,tx,ty;
int n,m,Q;
bool f;

struct Node{int x,y,xx,yy,t;};//t 是一个时间戳，用来表示当前状态下的最小时间。

void BFS()
{
    if(sx==tx&&sy==ty){cout<<0<<endl;f=true;return ;}
    //若起点等于终点，直接特判即可。
    queue<Node>q;
    q.push(Node{sx,sy,ex,ey,0});
    memset(vis,0,sizeof(vis));//由于有 q 组询问，请不要忘记初始化。
    vis[sx][sy][ex][ey]=1;
    while(!q.empty())
    {
        Node now=q.front();
        q.pop();
        for(int i=0;i<4;i++)
        {
            int x=now.x,y=now.y;
            int nx=now.xx+dx[i];
            int ny=now.yy+dy[i];//更新空格的横纵坐标。
            if(x==nx&&y==ny){x=now.xx;y=now.yy;}//若棋子与空格交换位置，则需更新棋子当前位置。
            if(nx<=0||nx>n||ny<=0||ny>m)continue;//边界判断
            if(vis[x][y][nx][ny]||a[nx][ny]==0||a[x][y]==0)continue;//显然如果当前节点是障碍或者已经访问过则 continue。
            vis[x][y][nx][ny]=1;
            Node tmp=Node{x,y,nx,ny,now.t+1};
            q.push(tmp);
            if(x==tx&&y==ty)
            {
                cout<<now.t+1<<endl;f=true;return ;//若棋子移动到目标位置则直接输出时间并返回。
            }
        }
    }
}

int main()
{
    n=read();m=read();Q=read();
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            a[i][j]=read();
        }
    }
    while(Q--)
    {
        ex=read();ey=read();sx=read();sy=read();tx=read();ty=read();
        f=false;
        BFS();
        if(f==false)cout<<-1<<endl;//无解。
    }
    return 0;
}

单次询问时间复杂度为 \(O((nm)^2)\)，\(q\) 次询问时间复杂度 \(O(q(nm)^2)\)。

至此，我们就获得了 70pts 的好成绩！

接下来，我们介绍一些常见的卡常技巧：

开 O2。相信这个不用我多说；

使用快读快写，这里有封装好的模板：

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
    return x*f;
}

inline void write(int x)
{
    if(x<0){putchar('-');x=-x;}
    if(x>9)write(x/10);
    putchar(x%10+'0');
}

对于换行符，不要用 cout<<endl;，直接 putchar('\n');。

用了这些之后，我们就已经获得了 85pts 的好成绩，如图：

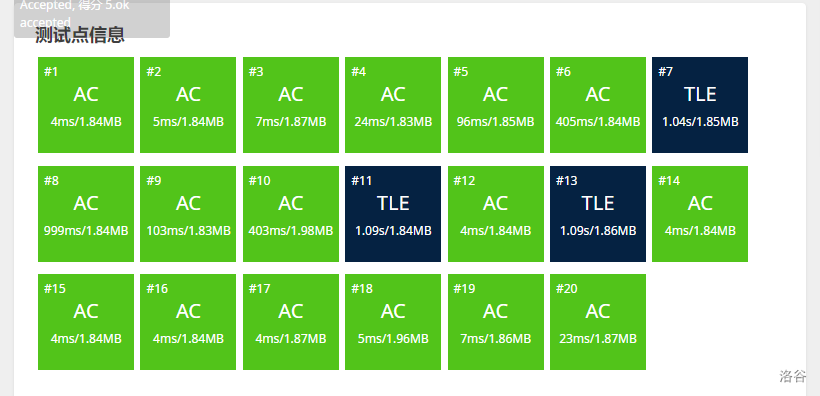
这里说明一下，其实当时我刚开始本来就想骗点暴力分然后打正解的。然后走到这一步，发现 T 了的三个点都在可观测范围之内，心里想：~~诶，我的程序卡一卡说不定有救……~~

~~然后就走上了一条卡常了 2 天然后 AC 的不归路（不是）。~~

走到这里之后的很长一段时间我此题的分数一直停留在 85pts 不变，正当我要放弃的时候，~~去讨论区瞅了一眼~~发现可以采用循环展开的方法，便有了如下代码（这里只提供了 BFS 部分，其它地方与上述代码相同）：

void BFS()
{
    if(sx==tx&&sy==ty){cout<<0<<endl;f=true;return ;}
    queue<Node>q;
    q.push(Node{sx,sy,ex,ey,0});
    memset(vis,0,sizeof(vis));
    vis[sx][sy][ex][ey]=1;
    while(!q.empty())
    {
        Node now=q.front();
        q.pop();
        int x,y,nx,ny;
        int i=0;
        x=now.x;y=now.y;
        nx=now.xx+dx[i];
        ny=now.yy+dy[i];
        if(x==nx&&y==ny){x=now.xx;y=now.yy;}
        if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
        {
            vis[x][y][nx][ny]=1;
            Node tmp=Node{x,y,nx,ny,now.t+1};
            q.push(tmp);
            if(x==tx&&y==ty)
            {
                write(now.t+1);putchar('\n');f=true;return ;
            }
        }
        i++;
        x=now.x;y=now.y;
        nx=now.xx+dx[i];
        ny=now.yy+dy[i];
        if(x==nx&&y==ny){x=now.xx;y=now.yy;}
        if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
        {
            vis[x][y][nx][ny]=1;
            Node tmp=Node{x,y,nx,ny,now.t+1};
            q.push(tmp);
            if(x==tx&&y==ty)
            {
                write(now.t+1);putchar('\n');f=true;return ;
            }
        }
        i++;
        x=now.x;y=now.y;
        nx=now.xx+dx[i];
        ny=now.yy+dy[i];
        if(x==nx&&y==ny){x=now.xx;y=now.yy;}
        if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
        {
            vis[x][y][nx][ny]=1;
            Node tmp=Node{x,y,nx,ny,now.t+1};
            q.push(tmp);
            if(x==tx&&y==ty)
            {
                write(now.t+1);putchar('\n');f=true;return ;
            }
        }
        i++;
        x=now.x;y=now.y;
        nx=now.xx+dx[i];
        ny=now.yy+dy[i];
        if(x==nx&&y==ny){x=now.xx;y=now.yy;}
        if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
        {
            vis[x][y][nx][ny]=1;
            Node tmp=Node{x,y,nx,ny,now.t+1};
            q.push(tmp);
            if(x==tx&&y==ty)
            {
                write(now.t+1);putchar('\n');f=true;return ;
            }
        }
    }
}

据说这样做相当于优化了 \(10^8\) 级别的常数。

于是我成功地拿到了 90pts：

可以发现，到现在为止，我们已经把两个的 TLE 都卡到了 0.05s 以内。

然后我们可以对于 i++ 这一步操作做一些改变，进行一点优化：

int x,y,nx,ny;
//int i=0;
x=now.x;y=now.y;
nx=now.xx;ny=now.yy-1;
if(x==nx&&y==ny){x=now.xx;y=now.yy;}
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
{
    vis[x][y][nx][ny]=1;
    Node tmp=Node{x,y,nx,ny,now.t+1};
    q.push(tmp);
    if(x==tx&&y==ty)
    {
        write(now.t+1);putchar('\n');f=true;return ;
    }
}
x=now.x;y=now.y;
nx=now.xx;ny=now.yy+1;
if(x==nx&&y==ny){x=now.xx;y=now.yy;}
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
{
    vis[x][y][nx][ny]=1;
    Node tmp=Node{x,y,nx,ny,now.t+1};
    q.push(tmp);
    if(x==tx&&y==ty)
    {
        write(now.t+1);putchar('\n');f=true;return ;
    }
}
//i++;
x=now.x;y=now.y;
nx=now.xx+1;ny=now.yy;
if(x==nx&&y==ny){x=now.xx;y=now.yy;}
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
{
    vis[x][y][nx][ny]=1;
    Node tmp=Node{x,y,nx,ny,now.t+1};
    q.push(tmp);
    if(x==tx&&y==ty)
    {
        write(now.t+1);putchar('\n');f=true;return ;
    }
}
//i++;
x=now.x;y=now.y;
nx=now.xx-1;ny=now.yy;
if(x==nx&&y==ny){x=now.xx;y=now.yy;}
if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])
{
    vis[x][y][nx][ny]=1;
    Node tmp=Node{x,y,nx,ny,now.t+1};
    q.push(tmp);
    if(x==tx&&y==ty)
    {
        write(now.t+1);putchar('\n');f=true;return ;
    }
}

省去了变量 \(i\) 以及 \(i++\) 的操作。于是：

……………………

…………

……

第十一个点 1s…………。

想起来一句歌词：

卡常卡不过，优化这，优化那，却还多那一两秒~ ——《WC 2019 OI 之梦》

然后我又思考了好久好久，优化了一些小的内容，但是都没能卡进这一秒的时限……

后来，当我几乎要放弃的时候，盯着程序看了好久，突然发现了一个东西：

对于当前状态是否可行（即是否可以入队）判断时，我们有一句代码：

if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny]&&a[x][y])

前四个是判断边界，第三个是判断之前是否走过该状态，最后两个分别判断空格和棋子是否走到一个障碍点。

但实际上！我们并不需要最后一个判断！因为棋子所在位置一定不可能是障碍物，因为在整个过程中棋子只有可能在原初始坐标或者与空格交换，但是这两种情况下棋子所在都不可能障碍位置！

于是，我怀着激动兴奋的心情删去了最后那一句判断，于是：

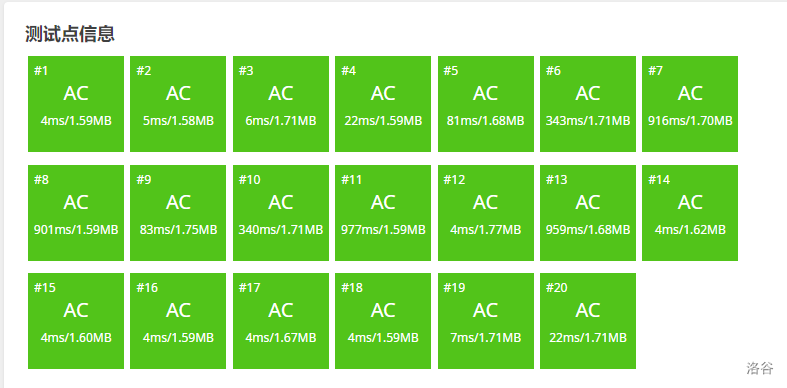
AC 了！！！！！！！！！！！！！！！！！！！！！

第十一个点以 977ms 的优异成绩卡进了时限！

我不得不说，十年前的题，放在现在快到飞起的评测机下，搜索 AC 也完全不是不可能。

总结

在一些题目正解想不到或者写起来很难写的情况下，不妨考虑搜索剪枝，虽然有时候说这是投机取巧，但不排除这种方式反而有可能在赛场上为你得到高分。
一些常用的卡常技巧：
- 快读快写；
- O2 优化；
- 循环展开；
- 换行符用 putchar('\n');
- 对于类似 \(i++\) 类语句可以想办法减少或者不用；
- 变量名可以定义在循环外面（虽然说我并没有在思路分析中说，但实际上我的 AC 代码中可以体现出来，下见 AC 代码）；
- 去掉一些不必要的判断条件。

代码实现

//luoguP3716
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int maxn=34;
int a[maxn][maxn],dis[maxn];
bool vis[maxn][maxn][maxn][maxn];
//int dx[4]={0,0,1,-1};
//int dy[4]={-1,1,0,0};
int ex,ey,sx,sy,tx,ty;
int n,m,Q;
bool f;

struct Node{int x,y,xx,yy,t;};

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

inline void write(int x)
{
    if(x<0){
    	putchar('-');
		x=-x;
	}
    if(x>9)
		write(x/10);
    putchar(x%10+'0');
}

void BFS()
{
	if(sx==tx&&sy==ty){cout<<0<<'\n';f=true;return ;}
	queue<Node>q;
	q.push(Node{sx,sy,ex,ey,0});
	memset(vis,0,sizeof(vis));
	vis[sx][sy][ex][ey]=1;
    int x,y,nx,ny;//变量定义在循环外部。
	while(!q.empty())
	{
		Node now=q.front();
		q.pop();
		//int i=0;
		x=now.x;y=now.y;
		nx=now.xx;ny=now.yy-1;
		if(x==nx&&y==ny){x=now.xx;y=now.yy;}
		if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny])
		{
			vis[x][y][nx][ny]=1;
			Node tmp=Node{x,y,nx,ny,now.t+1};
			q.push(tmp);
			if(x==tx&&y==ty)
			{
				write(now.t+1);putchar('\n');f=true;return ;
			}
	    }
		x=now.x;y=now.y;
		nx=now.xx;ny=now.yy+1;
		if(x==nx&&y==ny){x=now.xx;y=now.yy;}
		if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny])
		{
			vis[x][y][nx][ny]=1;
			Node tmp=Node{x,y,nx,ny,now.t+1};
			q.push(tmp);
			if(x==tx&&y==ty)
			{
				write(now.t+1);putchar('\n');f=true;return ;
			}
		}
		//i++;
		x=now.x;y=now.y;
		nx=now.xx+1;ny=now.yy;
		if(x==nx&&y==ny){x=now.xx;y=now.yy;}
		if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny])
		{
			vis[x][y][nx][ny]=1;
			Node tmp=Node{x,y,nx,ny,now.t+1};
			q.push(tmp);
			if(x==tx&&y==ty)
			{
				write(now.t+1);putchar('\n');f=true;return ;
			}
		}
		//i++;
		x=now.x;y=now.y;
		nx=now.xx-1;ny=now.yy;
		if(x==nx&&y==ny){x=now.xx;y=now.yy;}
		if(nx>=1&&nx<=n&&ny>=1&&ny<=m&&!vis[x][y][nx][ny]&&a[nx][ny])
		{
			vis[x][y][nx][ny]=1;
			Node tmp=Node{x,y,nx,ny,now.t+1};
			q.push(tmp);
			if(x==tx&&y==ty)
			{
				write(now.t+1);putchar('\n');f=true;return ;
			}
		}
	}
}

int main()
{
    //ios::sync_with_stdio(false);
	n=read();m=read();Q=read();
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			a[i][j]=read();
		}
	}
	while(Q--)
	{
		ex=read();ey=read();sx=read();sy=read();tx=read();ty=read();
		f=false;
		BFS();
		if(f==false){write(-1);putchar('\n');}
	}
	return 0;
}

后记

这道题我从 5.27 下午调到 5.28 下午，提交了 50 多遍，创下了我提交次数最多的题目的记录。只有我自己知道有多艰辛。

我的提交记录：

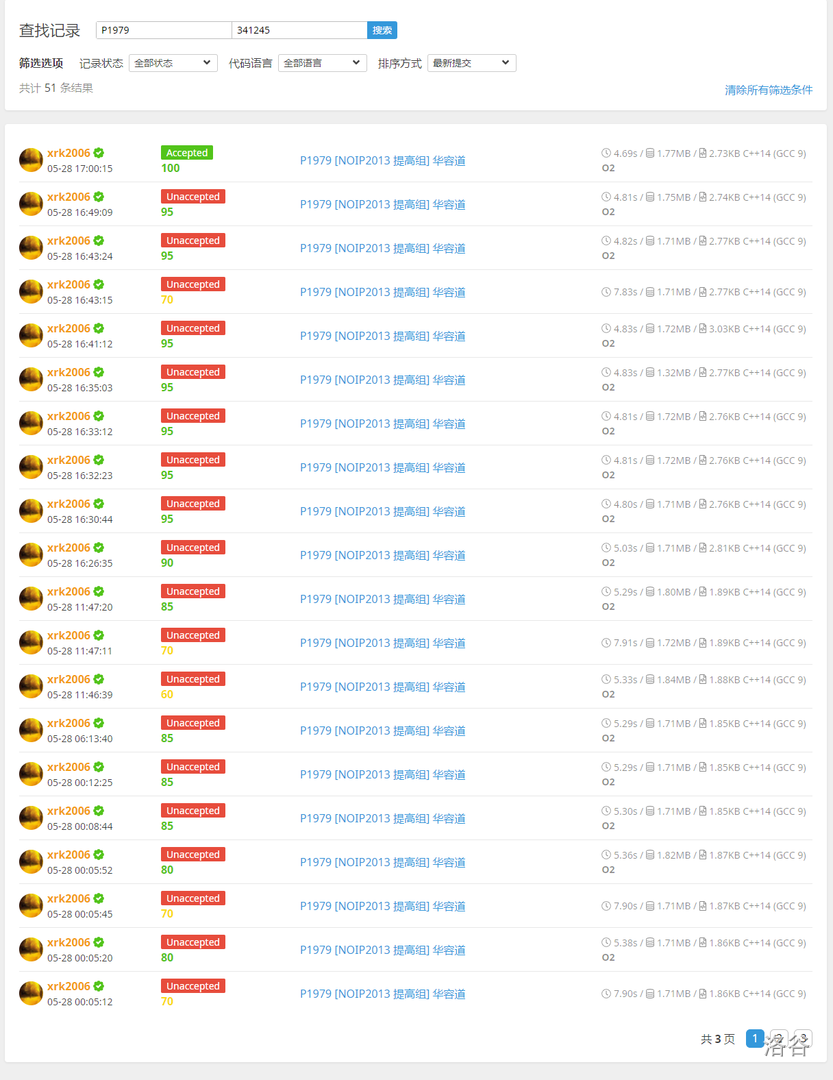
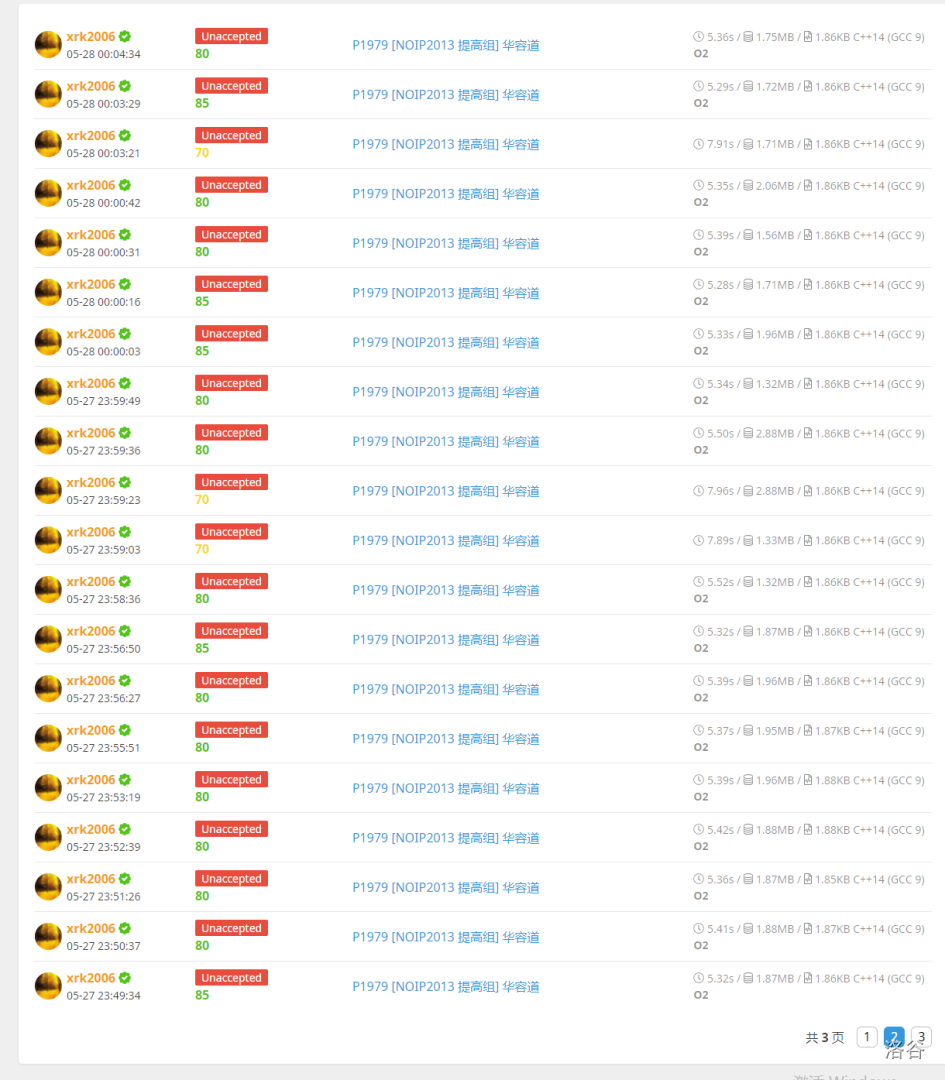
但 OI 就是这样，虽然 OI 知识艰涩难懂，虽然 OI 题目难入登天，但每个 OIer 都怀着那份对 OI 最纯粹的热爱，义无反顾地走在这条孤独的道路上，未曾说过放弃。

我也是如此，入坑 OI 两年了，虽然还是很菜，虽然还是一次次的被吊打，一次次的经历挫折，但是问我是否后悔，我还是会坚定地说出：

此生无悔入 OI，来世还做信竞人。

热爱和信仰。

posted @ 2022-06-02 17:28 向日葵Reta 阅读(98) 评论(2) 编辑收藏举报

刷新页面返回顶部

向日葵Reta

xrk's blog