【文化课学习笔记】【数学】解析几何之圆锥曲线解答题解题套路技巧方法

【数学】解析几何之圆锥曲线解答题解题套路技巧方法

轨迹方程

问题特征

已知某动点满足的几何条件，求该动点的轨迹方程（该动点形成的图形的方程）。即：未知轨迹图形。

求解方法

定义法

1. 适用范围：可以直接看出/猜测出动点满足的轨迹图形，即题目给定的条件符合某种圆锥曲线的定义。例如题目中有明显的条件可以猜测动点对应的轨迹方程是椭圆/双曲线/抛物线。
2. 步骤：
   • 根据题目条件猜测是哪种圆锥曲线，并根据条件验证猜测的正确，或根据该种圆锥曲线的特点反推出题目条件是否满足该圆锥曲线；
   • 根据定义求出圆锥曲线的方程；
   • 排除掉不符合要求的点的集合：可以根据题目条件排除（双曲线的一支），或某些特殊点（圆锥曲线顶点、与两坐标轴交点）。

代数法

1. 适用范围：题目给定的条件与某种曲线无关。

2. 步骤：

   求动点 \(P\) 的轨迹方程：

   • 设点 \(P\) 的坐标为 \(P(x,y)\)；
   • 对题目条件进行「几何条件代数化」，将几何条件翻译成对应的代数式，化简整理得到关于 \(x,y\) 的方程。
   • 排除掉不符合要求的点的集合：可以根据题目条件排除（双曲线的一支），或某些特殊点（圆锥曲线顶点、与两坐标轴交点）。

   其中在第二步「几何条件代数化」时，有三种解题方法。

   【直译法】即，题目中已知的几何条件可以直接翻译成代数式，例如：告诉某两个直线的斜率之积为 \(-\dfrac{1}{2}\)，可以直接翻译为 \(k_1 \cdot k_2 =-\dfrac{1}{2}\)。一些小 trick：遇到圆中弦长考虑作弦心距利用垂径定理。

   【相关点法】一般运用于「多动点问题」，此时应该把所有的动点都设出来，要求的动点设为 \((x,y)\)，其它动点可能可以用已知条件和已设出动点的坐标表示，也有可能需要重新设变量表示。特点是字母较多，可能需要更多的消元。

   【消参法】题目中有参数应该要最后消掉参数，同时求轨迹方程时还要考虑参数的范围，需要根据参数的范围求出轨迹方程中自变量的范围。

双动点问题（韦达定理）

1. 问题特征：直线和圆锥曲线有两个交点，且这两个交点均为动点。

2. 基本方法：

   • 设出直线方程；
   • 联立直线与圆锥曲线方程，得到一元二次方程；
   • 根据 \(\Delta >0\) 利用韦达定理列式；
   • 将几何条件翻译为代数式，结合韦达定理，解决问题。

3. 设直线方程的要点：

   • 已知直线斜率为 \(k\)，设 \(y=kx+b\)；
   • 已知直线过 \(y\) 轴上一点 \((0,b)\)，设 \(y=kx+b\)，需要讨论斜率不存在（竖直直线）的情况；
   • 已知直线过 \(x\) 轴上一点 \((t,0)\)，设 \(x=my+t\)，需要讨论斜率 \(=0\)（水平直线）的情况；
   • 已知直线过非坐标轴上一点 \((x_0,y_0)\)，设 \(y-y_0=k(x-x_0)\)，需要讨论斜率不存在的情况。

4. 得到一元二次方程后有关 \(\Delta >0\) 要点：

   • 如果从几何上能直接判断直线与圆锥曲线必有两个交点，可以不写；

   • \(\Delta >0\) 作用：

     【求值】验证是否满足 \(\Delta >0\)，不满足要舍去；

     【求范围】\(\Delta>0\) 是答案的一部分，一个限制条件；

     【其它】保证不扣分。

5. 其它解题要点：

   • 联立直线与圆锥曲线方程，有分母的方程可以直接去掉简化运算；
   • 一般情况下，题目中已知的「等腰三角形」可以利用三线合一的性质进行转化。例如：若已知 \(|PM|=|PN|\)，则可以作 \(PH \perp MN\)，然后利用 \(k_{PH}\cdot k_{MN}=-1\) 或其它几何条件求解；
   • 若已知两条直线 \(l_1\) 和 \(l_2\) 关于一条水平直线对称，则有 \(k_{l_1}+k_{l_2}=0\)。
   • 将几何条件翻译成代数式后，对代数式的计算为了防止出错可以先消掉其中的 \(x\) 或 \(y\)，保留需要的 \(y\) 或 \(x\)，计算时应该先合并同类项后再代入韦达定理算出来的结果。
   • 上一步消去参数时，除了可以选用「直线方程」，例如将 \(y\) 用 \(kx+b\) 替换，在抛物线中也可以选用「抛物线方程」。
   • 计算过程中遇到需要去分母的问题，要注意分母不能等于 \(0\)。
   • 若翻译后得到的代数式是非对称方程，可以通过解方程组的方法消元，消掉 \(x\) 求得 \(k\)。

常见几何条件的转化方式

位置关系

1. 三点共线：例如，题目告诉 \(A,P,Q\) 三点共线。一般情况下有以下三种转化方式：

   未知直线 \(PQ\) 方程时：

   • \(k_{AP} = k_{AQ}\)，需要讨论斜率不存在，尽量可以选择不适用。
   • \(\overrightarrow{AP}\parallel \overrightarrow{AQ}\)；

   已知直线 \(PQ\) 方程时：

   • \(A\in l_{PQ}\)，即点 \(A\) 的坐标满足直线 \(PQ\) 的方程。

2. 垂直关系：例如，在下图中，椭圆 \(C:\dfrac{x^2}{4}+\dfrac{y^2}{3} = 1\)，\(l_{AB}:y=kx-1\)，\(A(x_1,y_1),B(x_2,y_2)\)，已知 \(OA\perp OB\)（或点 \(O\) 在以 \(AB\) 为直径的圆上）。

   

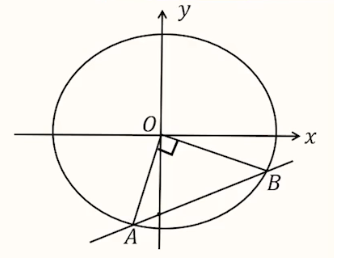
   则有两种转化方式：

   • \(k_{OA} \cdot k_{OB}=-1\)；
   • \(\overrightarrow{OA}\cdot \overrightarrow{OB}=0\)。

角关系

1. 锐角：例如已知 \(\angle AOB\) 为锐角（或点 \(O\) 在以 \(AB\) 为直径的圆外），可以翻译为：\(\overrightarrow{OA}\cdot \overrightarrow{OB} >0\)，且 \(O,A,B\) 不共线；

2. 钝角：例如已知 \(\angle AOB\) 为钝角（或点 \(O\) 在以 \(AB\) 为直径的圆内），可以翻译为：\(\overrightarrow{OA}\cdot \overrightarrow{OB} <0\)，且 \(O,A,B\) 不共线；

3. 其它情况：利用倾斜角转化为斜率。具体而言：

   • 等角：当两个角相等，有一条公共边且这条边在 \(x\) 轴或 \(y\) 轴上时，两个角对应的另外两条边所在直线 \(l_1\) 和 \(l_2\) 满足 \(k_{l_1}+k_{l_2}=0\)。

   • 其它角：例如，在下图中，直线 \(l_1\) 的斜率为 \(k_1\)，直线 \(l_2\) 的斜率为 \(k_2\)，则：

     \[\tan \gamma = \tan (\beta - \alpha) = \dfrac{\tan \beta - \tan \alpha}{1 + \tan \beta \tan \alpha} = \dfrac{k_2 - k_1}{1 + k_1k_2} \]

等腰三角形

例：如图，已知椭圆 \(C:\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1,l_{AB}:y=kx-1,A(x_1,y_1),B(x_2,y_2)\)，设点 \(P(4,1)\)，且 \(|PA|=|PB|\)。

转化方式：取 \(AB\) 中点 \(M\)，则 \(PM \perp AB\)，即 \(k_{PM}\cdot k_{AB} = -1\)。

求解 \(k_{PM}\) 时可以采用如下方法：

根据问题满足「双动点问题」的特征，可以利用韦达定理求出 \(x_1 +x_2\) 和 \(x_1\cdot x_2\)，然后根据 \(M\) 是 \(AB\) 中点写出 \(M\) 坐标与 \(AB\) 坐标的等量关系并代入韦达定理表示，然后利用斜率公式求解。

平行四边形

例：如图，已知椭圆 \(C:\dfrac{x^2}{4}+\dfrac{y^2}{3}=1,l_{AB}:y=kx-1,A(x_1,y_1),B(x_2,y_2)\)，在椭圆上存在点 \(M\)，使得四边形 \(OAMB\) 是四边形。

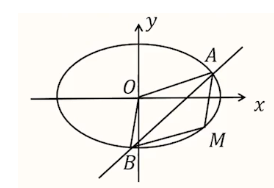
有两种常见的转化方式：

• \(\overrightarrow{OB} = \overrightarrow{AM}\)；
• \(\overrightarrow{OA} + \overrightarrow{OB} = \overrightarrow{OM}\)，且 \(O,A,B\) 不共线。

说明：对于菱形/矩形可以转化为「平行四边形+邻边相等」和「平行四边形+邻边垂直」来处理。

对称关系

例：如图，已知椭圆 \(C:\dfrac{x^2}{4} + \dfrac{y^2}{3} = 1\)，椭圆上两点 \(A,B\) 关于直线 \(l:y=2x+6\) 对称，其中 \(A(x_1,y_1),B(x_2,y_2)\)。

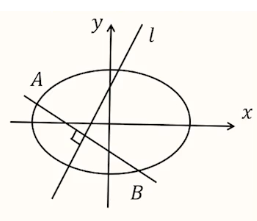
有两种常见的转化方式：

• \(AB \perp l\)：\(k_{AB}\cdot k_l=-1\)，可以求出 \(k_{AB}\)，从而设出 \(AB\) 方程与椭圆方程联立利用韦达定理。
• \(AB\) 中点 \(M\) 在直线 \(l\) 上：在上一条的基础上，用 \(A,B\) 坐标和 \(l_{AB}\) 的方程表示出 \(M\) 的坐标并带入到直线 \(l\) 的方程，得到关于 \(b\) 的方程。

弦长公式

例：如图，\(A(x_1,y_1),B(x_2,y_2)\)，\(k\) 为 \(l_{AB}\) 的斜率，\(|AB|=5\)。

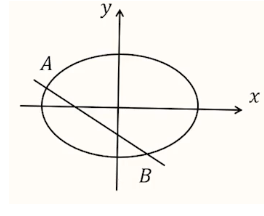
转化方式：弦长公式，设横截式中 \(m=\dfrac{1}{k}\)，则：

\[|AB|=\sqrt{1+k^2}|x_1-x_2|=\sqrt{1+\dfrac{1}{k^2}}|y_1-y_2|=\sqrt{1+m^2}|y_1-y_2| \]

两种情况，第一种情况适用于斜截式，第二种情况适用于横截式。

其中，联立圆锥曲线方程与直线方程得到一元二次方程后，若方程未知数为 \(x\)，有 \(|x_1-x_2|=\dfrac{\sqrt{\Delta}}{|a|}\)，若方程未知数为 \(y\)，亦有：\(|y_1-y_2|=\dfrac{\sqrt{\Delta}}{|a|}\)。

说明：对于相互垂直且共端点的两条弦长所在直线，将其中一个利用弦长公式表达的弦长中的 \(k\) 全部替换为 \(\dfrac{1}{k}\)，就可以得到第二个弦长表达式。

更一般地，对于直线方程 \(l_1:y=k(x+b)\) 和 \(l_2:y=(k+t)(x+b)\)，将直线 \(l_1\) 截椭圆得到的弦长利用弦长公式表示后，将其中的 \(k\) 换成 \(k+2\) 就是 \(l_2\) 截得的弦长表达式。

注意：当两点之间的斜率已知时，也可以用弦长公式求两点间距离。

面积关系

1. 已知具体的面积：例：如图，已知椭圆 \(C:\dfrac{x^2}{4} + \dfrac{y^2}{3}=1\)，\(l_{AB} : y=kx-1,A(x_1,y_1),B(x_2,y_2)\)，已知 \(S_{\triangle OAB}=4\)。

   

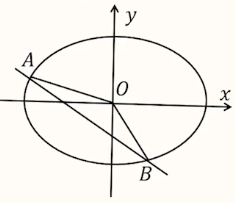
   转化方式：过点 \(O\) 作 \(AB\) 的垂线，即为 \(\triangle OAB\) 中 \(AB\) 上的高 \(h\)，则 \(|AB|=\sqrt{1+k^2}|x_1-x_2|,h=d_{0\to AB} = \dfrac{|-1|}{\sqrt{1+k^2}},S_{\triangle OAB}=\dfrac{1}{2}\cdot AB\cdot h=\dfrac{1}{2}|x_1-x_2|\)。

   说明：若题目给定四边形的面积，可以将四边形切割成三角形进行转化。

2. 面积之比：例：同上图，已知椭圆 \(C:\dfrac{x^2}{4} + \dfrac{y^2}{3}=1\)，\(l_{AB} : y=kx-1,A(x_1,y_1),B(x_2,y_2)\)，已知直线 \(AB\) 与 \(x\) 轴交于点 \(M\)，且 \(S_{\triangle AOM} = 4S_{\triangle BOM}\)。

   转化方式：先将面积比转化成线段比，即

   \[\dfrac{S_{\triangle AOM}}{S_{\triangle BOM}}=4 \implies \dfrac{AM}{BM} = 4 \implies \overrightarrow{AM} = 4\overrightarrow{MB} \]

   利用 \(l_{AB}\) 的方程求出 \(M\) 用 \(k\) 表示的坐标，并代入上述式中。

三角形重心

例：如图，\(G\) 是 \(\triangle ABC\) 的重心。

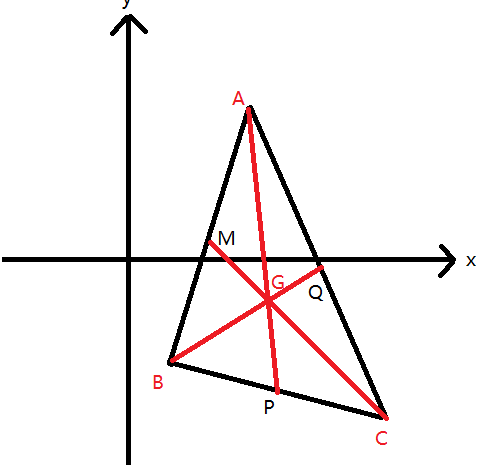
转化方式：

• \(x_G = \dfrac{1}{3}(x_A + x_B + x_C),y_G = \dfrac{1}{3}(y_A+y_B + y_C)\)；
• \(\overrightarrow{AM}=\overrightarrow{MB},\overrightarrow{BP} = \overrightarrow{PC},\overrightarrow{AQ} = \overrightarrow{QC}\)；
• \(|AG|:|GP|=|BG|:|GQ|=|CG|:|GM|=2:1\)。

单动点问题

问题特征

直线和圆锥曲线有两个交点，且这两个交点一定一动。

求解方法

1. 设直线：

   【适用范围】较为常用、一般的解法，直线和圆锥曲线相交，几何条件不容易用点坐标翻译。

   【步骤】

   • 设出直线方程；
   • 联立直线与圆锥曲线方程，得到一元二次方程；
   • 根据 \(\Delta >0\) 利用韦达定理列式；
   • 根据顶点坐标已知求出动点坐标（通常选择两根之积，已知的根为 \(0\) 时选择两根之和），利用动点坐标解题。

2. 设点：

   【适用范围】

   • 动点数量较少，且几何条件容易用点坐标翻译；
   • 没有直线与圆锥曲线相交。

   【步骤】

   • 设出动点坐标；
   • 写出动点满足的圆锥曲线方程；
   • 将题目中的几何条件用点翻译成代数式；
   • 利用翻译出来的式子观察求解。

范围类问题

解决方法

1. 不等式：适用于题目条件可以转化成不等式，例如：告诉锐角、点在椭圆内或 \(\Delta >0\)。
2. 函数：图形会运动，条件符合函数的定义，可以表示成某个东西的函数。注意：此时要求出函数的定义域。

利用函数求解范围类问题的一般思路

1. 将所求量表示成一个函数：通常设谁，就表示成谁（\(k/m/x_0,y_0\)）的函数。

   特别注意：找准函数的定义域（自变量的取值范围）。

2. 求函数值域/最值。

求值域/最值方法总结

【类型一：可以直接求解】

求解方法：按照函数计算顺序直接求解范围。

注意事项：需要注意题目中容易忽视的范围。例如反比例函数 \(y= \dfrac{1}{x}\) 中，\(y\) 恒大于 \(0\)；\(y=\sqrt{x}\) 中 \(x\) 恒大于等于 \(0\) 等。

例：求函数 \(y = \dfrac{1}{4k^2+3}\) 的范围。

那么：

\[4k^2 + 3 \ge 3 \longrightarrow 0 < y \le \dfrac{1}{3} \]

该函数由 $ x= 4k^2 + 3$ 和 \(y=\dfrac{1}{x}\) 复合而成。注意：\(y>0\) 不要漏掉。

*【类型二：分子不为常数的分式型函数】

核心技术：

• 拆分：处理分子或分母是单项式的函数；
• 分离系数：分子和分母都是多项式的函数。

辅助手段：

• 换元（注意写范围）；
• 均值不等式/对勾函数。

求解步骤：

• 先观察分子/分母有没有单项式：若有，则对分式进行拆分。

  若分母是单项式，直接拆分。

  例如：求 \(y = \dfrac{3k^2+2k+1}{k^2}(k>0)\) 的范围。

  那么有：

  \[y = \dfrac{3k^2+2k+1}{k^2} = \dfrac{3k^2}{k^2} + \dfrac{2k}{k^2} + \dfrac{1}{k^2} = 3 + \dfrac{2}{k} + \dfrac{1}{k^2} \]

  将原函数转化为有关 \(\dfrac{1}{k}\) 的二次函数。则令 \(t=\dfrac{1}{k}\)，那么 \(t>0\)（不要忘掉范围），有：

  \[y= t^2 + 2t + 3>3 \]

  若分子是单项式，分子分母同时除以分子（需要考虑分子是否为 \(0\)）。

  例如：求 \(y = \dfrac{k^4}{k^4 + k^2 + 1}\) 的范围。

  当 \(k=0\) 时，\(y=0\)。

  当 \(k\ne 0\) 时，有：

  \[y = \dfrac{1}{\dfrac{k^4 + k^2 +1}{k^4}} = \dfrac{1}{1 + \dfrac{1}{k^2} + \dfrac{1}{k^4}} \]

  令 \(t = \dfrac{1}{k^2}(t>0)\)，则：

  \[y = \dfrac{1}{t^2 + t +1} \ce{->[t^2 + t + 1>1]} 0<y<1 \]

  综上，\(y \in [0,1)\)。

  化简函数之后不一定会转化为二次函数求值域，也可能转化为对勾函数或基本不等式。

  例如：求 \(y = \dfrac{k^2}{k^4 + k^2 +1}\)，\(k \in [1,+\infty)\) 的最大值。

  则：

  \[y = \dfrac{1}{k^2 + \dfrac{1}{k^2} + 1}\ce{->[k^2 + \frac{1}{k^2}\ge 2\cdot\sqrt{k^2\cdot \frac{1}{k^2}}=2]} y_{\max} = \dfrac{1}{3} \]

  注意在使用基本不等式时，需要验证等号是否能取到，例如在此题中就是 \(k^2 = \dfrac{1}{k^2}\) 时，\(k = 1\)，可以取到。

  若等号不能取到，则应利用对勾函数，根据对勾函数的图像求函数取值范围。

  对于分子/分母存在绝对值的函数，可以将其它没有绝对值的自变量也加上绝对值。

  例如：求 \(S = \dfrac{36|k|}{4k^2 + 3}(k\ne 0)\) 的最大值。

  那么：

  \[S = \dfrac{36|k|}{4|k|^2 + 3} = \dfrac{36}{4|k| + \dfrac{3}{|k|}} \longrightarrow 4|k| +\dfrac{3}{|k|} \ge 2\sqrt{4|k| \cdot \dfrac{3}{|k|}} = 4\sqrt{3} \longrightarrow S_{\max} = \dfrac{36}{4\sqrt{3}}= 3\sqrt{3} \]

  等号成立时 \(k = \pm \dfrac{3}{2}\)，可以取到。

• 分子分母都是多项式时：

  观察分子或分母是否可以通过换元从而换成单项式，从而把另一个分母或分子用换元之后的自变量表示。

  例如：求 \(S = 2\sqrt{3}\dfrac{\sqrt{1+k^2}}{4+k^2}\) 的范围。

  令 \(t = \sqrt{1 + k^2}\)，\(t \ge 1\)，则：

  \[S = 2 \sqrt{3}\cdot \dfrac{t}{t^2+3} \]

  然后按照分子为单项式的方法求解即可。

  若另一个分子或分母不能用换元之后的自变量表示。则考虑使用分离系数。

  例：求 \(y = \dfrac{2k^4 + 7k^2 + 10}{k^4 + 3k^2 + 4}\) 的最大值。

  则：

  \[y = \dfrac{2k^4 + 7k^2 + 10}{k^4 + 3k^2 + 4} = \dfrac{2(k^4 + 3k^2 + 4)+ k^2 +2}{k^4 + 3k^2 +4} = 2+ \dfrac{k^2 + 2}{k^4 + 3k^2 +4} \]

  令 \(t= k^2 + 2\)，\(t\ge 2\)，则 \(k^2 = t-2\)。

  那么：

  \[y = 2 + \dfrac{t}{(t-2)^2 + 3(t-2) + 4} = 2 + \dfrac{t}{t^2 - t +2} = 2 + \dfrac{1}{t+ \dfrac{2}{t} -1} \]

  再用对勾函数求解。

总结：

1. 若分子分母都为多项式（不都为多项式跳过此步）：观察分子或分母是否可以通过换元从而换成单项式，若不能换元，则用分离常数；反之将分子或分母换元成单项式。
2. 若分子/分母存在绝对值（无绝对值跳过此步）：将其它没有绝对值的自变量也加上绝对值。
3. 若分母是单项式：直接拆分。
4. 若分子是单项式：上下同时除以分子。
5. 最后利用二次函数值域/对勾函数/均值不等式求解。

【类型三：求导】笔者还未学习导数，学完导数再来补充。

【类型四：一类需要单独记忆的函数】

例：求 \(f(k) = \dfrac{k^4 + 8k^2 + 1}{2k^3 + 2k}\)，\(k\ge 1\) 的最小值。

特点：

• 次数：

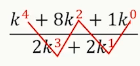
• 系数：
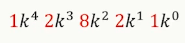
  ，呈现对称/回文。

求解方法：分子分母同时除以 \(k^2\)，凑出 \(k+ \dfrac{1}{k}\)。

求解：

\[f(k) = \dfrac{k^2 + \dfrac{1}{k^2} + 8}{2k+ \dfrac{2}{k}} = \dfrac{(k+ \dfrac{1}{k})^2 + 6}{2(k + \dfrac{1}{k})} \]

设 \(t = k + \dfrac{1}{k}\)，则 \(t\ge 2\)。接下来直接利用分母是单项式的做法求解。

定值问题

问题特征

题目要求证明某个东西是个定值。

基本方法

直接计算出某个东西的值。

解题技巧

1. 对于经过非坐标轴上点的直线，不仅可以设点斜式，还可以直接设斜截式 \(y=kx+b\)，这样代入到圆曲方程中时有时可以简化运算。
2. 对于判断「是否存在常数 \(\lambda\)，使得某式为定值」问题时，对于整式，可以对式中非 \(\lambda\) 的字母做合并同类项，然后令其系数为 \(0\) 求出 \(\lambda\) 的值；对于分式，除了利用「系数为 \(0\)」还可以考虑分子分母提出公因式，上下约分。即可以考虑上下对应系数成比例从而列出对应比例式建立方程求解。
3. 判断定值有时要考虑特殊情况：如斜率不存在，与 \(x\) 轴平行等情况。
4. 一般有两种基本的解题思路：设点/设直线。对于题目中动点较多的情况， 观察圆锥曲线上有几个动点，若只有一个动点，则设该动点可能是最好的方法。
5. 解决定值问题一种常见的解题方法是「先猜后证」，一般可考虑通过特殊位置猜到对应的结论，然后再证明与猜想相同。
6. 对于要证明某个角是定值的问题，一般证明的角度都是直角，可用向量点乘 \(=0\) 或斜率相乘为 \(-1\) 求解。
7. 定值问题设直线时，对于横截式最后一定要讨论与 \(x\) 轴平行的情况，对于斜截式一定要讨论斜率不存在的情况。

定点问题

问题特征

证明某个点是定点。

基本方法

方法一

消参法，求出定点坐标。

以求证直线 \(l\) 过定点为例：

1. 求出直线方程（带有参数）；
2. 按参数整理，例如当参数为 \(m\) 时，整理成 \(am +b = c\) 的形式，令系数 \(a\) 和 \(c\) 为 \(0\) 得定点。

方法二

先猜后证。

通常来讲，先猜出定点所在的坐标轴，再求定点。

例如：标答写法：由对称性，定点在 \(x\) 轴上。

猜出定点所在坐标轴，主要有以下两种方法：

1. 特殊直线：一般指水平直线/竖直直线。例如：\(l\) 与 \(x\) 轴重合时，满足题意 \(\to\) 定点在 \(x\) 轴上。
2. 对称性：一般将直线关于坐标轴对称观察其对称后的直线是否满足题目要求。如果两坐标轴均不满足题目要求，则不能用此方法猜出定点位置。例如：将直线 \(l\) 关于 \(x\) 轴对称，得到的直线 \(l'\) 依然满足题目所给的条件，而定点是 \(l\) 和 \(l'\) 的交点，所以定点在 \(x\) 轴上。

证明主要的步骤是：

1. 表示出直线上两点；
2. 用两点坐标表示出直线方程：若定点在 \(x\) 轴上，一般是横截式；若定点在 \(y\) 轴上，一般是点斜式；
3. 根据定点所在坐标轴，令 \(x=0\) 或 \(y=0\) 将对应 \(y\) 或 \(x\) 的表达式化为最简形式，再代入直线上两点，化简得到定点坐标。

解题技巧

1. 对于多条直线与圆锥曲线有交点的问题，要考虑「需要设哪些直线」，以及「哪些直线设了之后计算更容易」。
2. 证明某个点在某条定直线上的问题，大概率求得的其横坐标或纵坐标有一个为常数。
3. 化简式子后若得到非对称式，可以考虑将 \(x_1\cdot x_2\) 替换成 \(x_1+x_2\)，具体而言可以将 \(x_1+x_2\) 除以 \(x_1\cdot x_2\)，得到两者的关系，并替换求解。
4. 涉及到圆与坐标轴的交点的问题，可以考虑先设出交点坐标，然后利用「直径所对的圆周角是直角」列出对应向量点乘为 \(0\) 建立方程求解。

一些常见易错点与注意事项

1. 对于方程 \(\dfrac{x^2}{4} + \dfrac{y^2}{2} = 1\)，去分母时应为 \(x^2 + 2y^2=4\)，而非 \(2x^2 + y^2 = 4\)。
2. 计算包含 \(x_1,x_2,y_1,y_2\) 的式子时，将所有的式子合并同类项为需要的 \(x_1+x_2,x_1x_2\) 的方式再代入计算，这样不易出错。
3. 去分母每一项都要乘，分式平方上下都要平方。
4. 将圆锥曲线方程与直线方程联立之后得到的一元二次方程若为 \((1+4k^2)x^2 - 16kx +12 = 0\) 注意不要丢掉其中二次项系数 \(4k^2\) 上面的平方。
5. 求解某直线方程时，若最后得到了一个关于 \(k\) 的二次方程，若 \(k^2\) 是一个常数，则 \(k\) 有正负两个值，而不是一个。
6. 利用韦达定理时，\(x_1+x_2=-\dfrac{b}{a}\)，别忘记前面的负号。
7. 求两个数/线段的比值时，如果直接比无法求得结果，可以考虑将两者相加。
8. 若某两个未知数 \(a\) 和 \(b\) 以及另外两个点 \(a\) 和 \(c\) 的坐标满足一个形式相同的等式，例如 \(\dfrac{|2+ab|}{\sqrt{1+(a+b)^2}}=1,\dfrac{|2+ac|}{\sqrt{1+(a+c)^2}}=1\)，则说明 \(b\) 和 \(c\) 是方程 \(\dfrac{|2+ax|}{\sqrt{1+(a+x)^2}}=1\) 的两根。
9. 利用弦长公式求解某线段长时，注意 \(|x_1-x_2| = \dfrac{\sqrt{\Delta}}{|a|}\)，而非 \(\dfrac{\Delta}{|a|}\)。
10. 对于抛物线 \(y^2=4x\)，设抛物线上点 \((t^2,2t)\) 可以简化运算。
11. 求圆内弦长一定要想到垂径定理。
12. 告诉某点在某直线上，除了可以将该点代入到直线方程中之外，还可以考虑该点和直线上其它两点共线，从而利用斜率相等解决问题，有时可以简化运算。
13. 题目涉及某个角的取值范围问题时，如果题目中有现成的三角形以该角为内角，可以考虑求出该三角形的其中一个三角函数值来判断其取值范围。
14. 一般情况下，尽量避免计算代数式中只包含 \(x_1,y_1\) 但不包含 \(x_2,y_2\) 的线段。
15. 当已知一条线段上两个点的横坐标/或纵坐标和线段所在直线的斜率，要求线段长时，要善用弦长公式。
16. 注意焦距为 \(2\)，说明 \(2c=2\) 而非 \(c=2\)。
17. 直线与抛物线联立得到的一元二次方程，其二次项系数可能为 \(0\)，计算时需要考虑到这一点。
18. 解题时要多考虑题目隐含的条件，例如提到直线 \(AB\) 说明 \(A\) 不能与 \(B\) 共点，提到直线 \(l\) 与 \(y\) 轴交于某点，说明 \(l\) 不与 \(y\) 轴平行。
19. 涉及到同时含有 \(x_1\) 和 \(y_1\) 的式子，最好在比较早的时候就把代数式消元，从而得到一个只含有 \(x_1\) 或 \(y_1\) 的代数式，更方便计算。
20. 解题过程中遇到分式计算，除了可以通分外，若分母为单项式，可考虑拆分计算。
21. 遇到抛物线的题目，最后得到同时含有 \(x_1\) 和 \(y_1\) 的式子，除了可以利用直线方程消元，还可利用抛物线方程消元，通常此种情况下反而更简单。
22. \((a+b+c)^2 = a^2+b^2+c^2+2ab+2ac+2bc\)
23. 直线方程与圆锥曲线方程联立得到的一元二次方程，一定要弄清是关于 \(y\) 的还是 \(x\) 的不要弄反。