【文化课学习笔记】【化学】选必一：化学平衡

【化学】选必一：化学平衡

化学平衡状态

可逆反应

1. 概念：在相同条件下，既能向正反应方向进行，同时又能向逆反应方向进行的反应；
2. 符号：化学方程式中用“\(\ce{<=>}\)”表示。
3. 特征：
   • 双向性：分为方向相反的两个反应——正反应和逆反应；
   • 双同性：在同一条件下，正、逆反应同时进行；
   • 共存性：反应物的转化率小于 \(100\%\)，反应物与生成物共存。

化学平衡状态

1. 概念：在一定条件下的可逆反应中，当正、逆两个方向的反应速率相等，反应体系中所有参加反应的物质的质量或浓度保持恒定时，这个状态叫化学平衡状态。

   

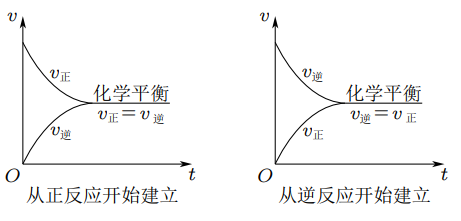
2. 建立：

   • 反应开始时：反应物的浓度最大，\(v(正)\) 最大，生成物的浓度为 \(0\)，\(v(逆)\) 为 \(0\)；
   • 反应进行时：反应物的浓度逐渐减小 \(\ce{->}\) \(v(正)\) 逐渐减小；生成物的浓度由 \(0\) 逐渐增大 \(\ce{->}\) 从 \(0\) 逐渐增大；
   • 达到平衡时：\(v(正)=v(逆)\)，反应混合物中各组分的你攻读保持不变。

   

3. 判断方法：

   可逆反应达到化学平衡状态由两个主要特征：

   • 正逆反应速率相等，即 \(v_正 = v_逆\)；
   • 变量不变，即达平衡，即某个平衡前变化的物理量（例如浓度、压强等）保持不变后，达到化学平衡。注意：原来不变的量不变不能说明达到化学平衡，例如气体体积前后不变时，不能说明气体体积不变时达到平衡的依据。

   以反应 \(\ce{m A(g) + n B(g) <=> p C(g) + q D(g)}\) 为例：

   【混合物体系中各成分的含量】

   • 当各物质的物质的量或物质的量分数一定时，达到平衡；
   • 当各物质的质量或质量分数一定时，达到平衡；
   • 当各气体的体积或体积分数一定时，达到平衡；
   • 总体积、总压强、总物质的量一定时，不一定达到平衡。

   【正、逆反应速率的关系】

   • 在单位时间内消耗了 \(\pu{m mol A}\)，同时生成了 \(\pu{m mol A}\)，达到平衡；
   • 在单位时间内消耗了 \(\pu{n mol B}\)，同时生成了 \(\ce{q mol D}\)，达到平衡；
   • \(v(\ce{A}):v(\ce{B}):v(\ce{C}):v(\ce{D}):m:n:p:q\)，不一定达到平衡（没有强调是 \(v_正\) 还是 \(v_逆\)）；
   • 在单位时间内生成了 \(\pu{n mol B}\)，同时消耗了 \(\ce{q mol D}\)，不一定达到平衡；
   • 单位时间内，同一物质断裂的化学键数与生成的化学键数相等时，达到平衡；

   【压强】

   • 恒温恒容且 \(m+n \ne p+q\)，当总压强一定时，达到平衡；
   • 恒温恒容且 \(m+n = p+q\)，当总压强一定时，不一定达到平衡。

   【混合气体的平均相对分子质量（\(\overline{M}\)）】注意不考虑固体。

   • \(\overline{M}\) 一定，且 \(m+n \ne p+q\) 时，达到平衡；
   • \(\overline{M}\) 一定，且 \(m+n = p+q\) 时，不一定达到平衡。

   【温度】在绝热体系中，当体系温度一定时，达到平衡。

   【体系的密度】恒温恒容条件下，当密度一定时，不一定达到平衡。（因为 \(\rho = \dfrac{m}{v}\)，纯气体反应体系中，总质量和体积都不变，所以密度无论是否达到平衡都始终不变）注意：只适用于纯气体反应体系，有液体/固体参与的反应不符合该规律。

   【颜色】含有有色物质的体系，当颜色不再变化时，达到平衡。

化学平衡常数

化学平衡体系中的反应物浓度与生成物浓度的关系

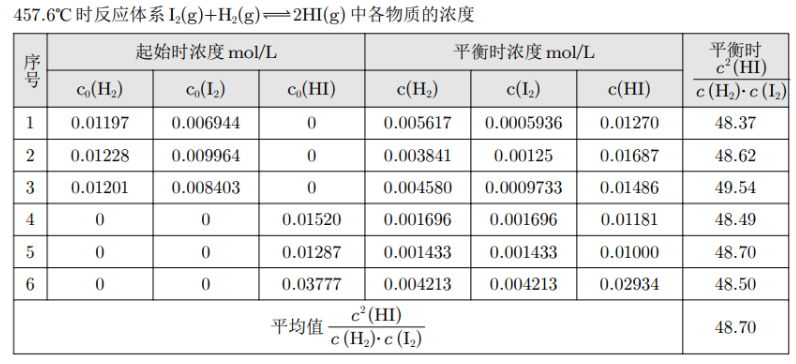
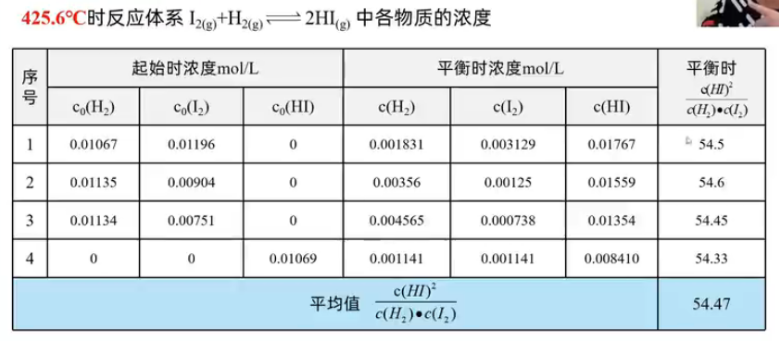
结论一：\(\dfrac{c^2(\ce{HI})}{c(\ce{H2})\cdot c(\ce{I2})}\) 为常数；

结论二：常数与反应物的起始浓度大小无关；与正向建立还是逆向建立平衡无关。

结论三：温度改变，该常数发生变化。

化学平衡常数

1. 概念：在一定温度下，当一个可逆反应达到化学平衡时，生成物浓度幂之积与反应物浓度幂之积与反应物浓度幂之积的比值是一个常数，用符号 \(K\) 表示。

   注意：是生成物幂之积与反应物幂之积之比，而不是反应物幂之积与生成物幂之积之比。

2. 表达式：对于反应 \(\ce{m A(g) + n B(g) <=> p C(g) + q D(g)}\)，在一定温度下达到平衡。

   平衡常数：

   \[K = \dfrac{c^p(\ce{C}) \cdot c^q(\ce{D})}{c^m({\ce{A}})\cdot c^n(\ce{B})} \]

   其中，\(c\) 为各组分的平衡浓度，温度一定，\(K\) 为定值。

3. 注意事项：

   • 对于有纯固体或纯液体参与的反应，纯固体或纯液体不列入平衡常数的表达式中；

     例如：对于稀薄水溶液中的水，水的浓度不变，不需要写入平衡常数。

   • 平衡常数是指某一具体反应的平衡常数。

     1. 若反应方向改变，则平衡常数改变（例如正逆反应的平衡常数互为倒数，即 \(K_1= \dfrac{1}{K_2}\)）；

     2. 若化学反应方程式中各物质的化学计量数等倍扩大或缩小，尽管是同一反应，平衡常数也会改变。系数变为原来的几倍，平衡常数变为原来的几次方，即对于一个反应若其平衡常数为 \(K_1\)，扩大 \(n\) 倍，最终新的平衡常数 \(K_2=(K_1)^n\)。

        方程式	\(\ce{\Delta H}\)	\(K\)
        逆写	等值异号（相反数）	倒数
        \(n\) 倍	\(n\) 倍	\(n\) 次方
        相加	相加	相乘

     3. 平衡常数表达式中 \(c(\ce{A})、c(\ce{B})、c(\ce{C})、c(\ce{D})\) 是指平衡时各物质的物质的量浓度，不可使用物质的量数据，且不可使用任意时刻的物质的量浓度数据。

     4. 有水参加或生成的反应的平衡常数表达式的书写：

        ①稀薄水溶液中的反应，如有水参加或生成，水的浓度不必写入平衡常数表达式。

        ②水为气态 \(\ce{[H2O(g)]}\) 需要写入平衡常数表达式中。

        ③非水溶液中进行的反应中，若有水参加或生成，则水的浓度应该出现在平衡常数的表达式中。例如：有机液体的反应 \(\ce{CH3COOH(l) + C2H5OH(l) <=> CH3COOC2H5(l) + H2O(l)}\)。

   • 计算有关平衡常数的计算时，要看清是正反应还是逆反应，单位是否相同（是否都是浓度，浓度的单位是否统一），前后温度是否不变（如果不变有可能可以通过平衡常数相同列方程）。

4. 意义：

   • 化学平衡常数是指在一定温度下一个反应本身固有的内在性质的定量表现，是表示可逆反应进行程度（限度）的一个特征值（注意是定量不是定性）；
   • \(K\) 越大，说明平衡体系中生成物所占的比例越大，正反应进行的程度越大，即该反应进行的越完全，平衡时反应物的转化率越大；\(K\) 越小，该反应进行的越不完全，平衡时反应物的转化率越小。
   • 一般来说，如果一个反应的平衡常数数值大于 \(10^5\)，通常认为该反应可以进行的较完全；相反，如果一个反应的平衡常数数值小于 \(10^{-5}\)，则认为这个反应很难进行。

5. 利用化学平衡常数判断平衡移动方向

   对于一般的可逆反应 \(\ce{m A(g) + n B(g) <=> p C(g) + q D(g)}\)，在任意状态（不是平衡）时，生成物与反应物的浓度幂之积的比值称为浓度商，用 \(Q\) 表示：

   \[Q=\dfrac{c^p(\ce{C})\cdot c^q(\ce{D})}{c^m(\ce{A})\cdot c^n(\ce{B})} \]

   用任意状态的浓度幂之积的比值 \(Q\) 与 \(K\) 比较，可判断可逆反应是否达到平衡状态和反应进行的方向，即：

   • 当 \(Q<K\)，反应向正方向移动；
   • 当 \(Q=K\)，反应处于平衡状态；
   • 当 \(Q>K\)，反应向逆方向移动。

化学平衡转化率

用平衡常数表示反应限度有时不够直观，因此实际应用中常用平衡转化率（\(\alpha\)）来表示一定条件下的反应限度：

\[某反应物的平衡转化率（\alpha）= \dfrac{该反应物平衡时已转化的量}{该反应物的起始总量}\times 100\% = \dfrac{该反应物的起始浓度 - 该反应物的平衡浓度}{该反应物的起始浓度}\times 100\% \]

影响化学平衡的因素与勒夏特列原理

化学平衡的移动

可逆反应达到平衡状态以后，若反应条件（如温度、压强、浓度等），平衡混合物中各组分的浓度也会随机改变，从而在一段时间后达到新的平衡状态。这种由原平衡向新平衡状态的变化过程，叫做化学平衡的移动。

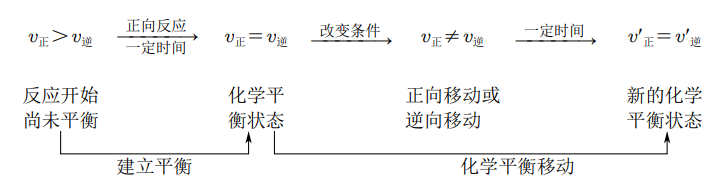
化学平衡移动方向的判断

1. 根据反应速率判断：若条件改变后：
   • \(v_正 > v_逆\)：平衡向正反应方向移动；
   • \(v_正 = v_逆\)：反应达到平衡状态，不发生平衡移动；
   • \(v_正 < v_逆\)：平衡向逆反应方向移动；
2. 根据 \(Q\) 与 \(K\) 判断：若条件改变后：
   • \(Q<K\)：平衡向正反应方向移动；
   • \(Q=K\)：反应达到平衡状态，不发生平衡移动；
   • \(Q>K\)：平衡向逆反应方向移动。
3. 根据勒夏特列原理。见下文。

勒夏特列原理与平衡移动方向

如果改变影响平衡的一个因素（如温度、压强，以及参加反应的物质的浓度），平衡就向着能够减弱（抵消）这种改变的方向移动。（概括起来就是多的就要减少少的就要增加）

【浓度】

• 增大反应物浓度或减小生成物浓度：向正反应方向移动；
• 减小反应物浓度或增大生成物浓度：向逆反应方向移动。

例如，对于反应 \(\ce{2CrO4^2- + 2H+ (aq) <=> CrO7^2- + H2O(l)}\)，其中铬酸根（\(\ce{CrO4^2-}\)）是黄色，重铬酸根（\(\ce{Cr2O7^2-}\)）是橙色。若该反应在平衡状态下，通入氯化氢气体，那么增加 \(\ce{H+}\) 浓度（因），平衡正向移动，铬酸根浓度减小，溶液由黄色逐渐变为橙色（果）。若在平衡状态下，加入氢氧化钠固体，那么 \(\ce{H+}\) 浓度减小，平衡逆向移动，铬酸根浓度增大，溶液由橙色变为黄色。

【压强（对于有气体存在的反应）】

注意事项：

1. 压强只影响气体，不影响固体和水溶液；
2. 如果涉及到压强对平衡的移动，先看反应前后气体计量数总和是否发生变化。
3. 加压/减压是通过压缩容器体积/减小容器体积来实现的，容器内所有物质的浓度都会增大/减小。

变化规律：

1. 若反应前后气体分子数改变：

   • 增大压强（压缩容器）：向气体计量数和较小的方向移动；
   • 减小压强（增大容器）：向气体计量数和较大的方向移动。

   口诀：大压小移，小压大移。

   注意：这里的“大压”和“小压”指的是通过压缩容器来加压减压，而不是通过加入稀有气体来加压减压。

   例如，对于反应 \(\ce{N2(g) + 3H2(g) <=> 2NH3(g)}\)，如果增大压强，那么由于正反应的反应物气体计量数之和大于逆反应的反应物气体计量数之和，所以正反应反应物的浓度增加幅度更大，平衡向正反应方向移动；或者也可以考虑当增大压强，\(v_正\) 增大幅度 \(>v_逆\)，平衡向正反应方向移动。

2. 若反应前后分子气体数不变：改变压强，平衡不移动。

【加入稀有气体】

• 恒温恒容：加入 \(\ce{He}\) 气，各物质浓度不变，平衡不移动；
• 恒温恒压：加入 \(\ce{He}\) 气，等同于增大容器体积减小压强的效果，向着气体计量数和大的方向移动。

【温度】

• 降低温度：环境温度降低，相当于要重新让环境温度升高，即要让体系向外界放热，那么向放热反应方向移动。
• 升高温度：同理，向吸热反应方向移动；

【催化剂】

使用催化剂，相当于可以等量降低正逆反应活化能，等量增加正逆反应速率，平衡不移动。

【对勒夏特列原理中“减弱”的正确理解】

1. 在已达平衡的可逆反应中，若增大某物质的浓度，则平衡向减少该物质的浓度的方向移动，则平衡向减少该物质的浓度的方向移动，移动的结果是该物质的浓度比原平衡的浓度大，即只能“减弱”不能“完全抵消”或反向移动。
2. 在已达平衡的可逆反应中，若增大平衡体系的压强（压缩容器体积），则平衡向减小压强的方向（气体总体积减小的方向）移动，移动的结果是新平衡的压强比原平衡的压强大。

化学平衡移动的图像分析

1. 浓度效应：\(\ce{a A(aq) + b B(aq) <=> p C(aq) + q D(aq)}\)

   技巧：化学反应

   【加入 \(\ce{A}\)】

   反应速率 - 时间图：

   

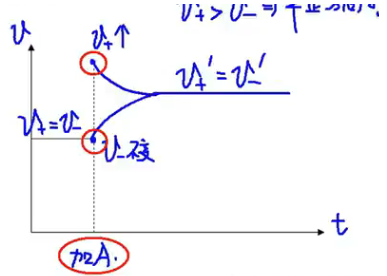
   浓度 - 时间关系图：

   

   【减少 \(\ce{A}\)】

   反应速率 - 时间图：

   

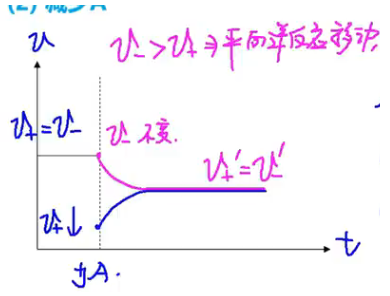
   浓度 - 时间图：

   

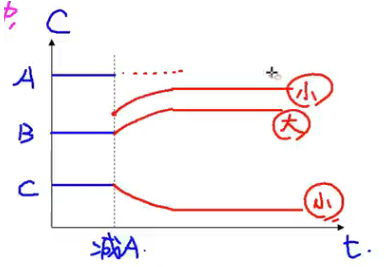
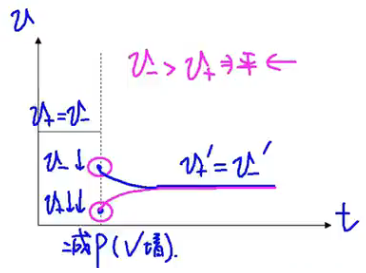
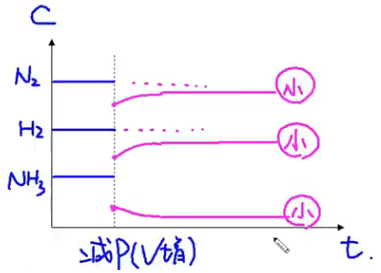
2. 压强效应：\(\ce{N2(g) + 3H2(g) <=> 2NH3(g)}\)

   技巧：压强对气体计量数和大者效果明显。压强增大/减小时，各个物质的浓度都增大/减小，正反应速率和你反应速率都增大/减小，即“雨露均沾”。

   【加压（缩小容器体积）】

   反应速率 - 时间图：

   

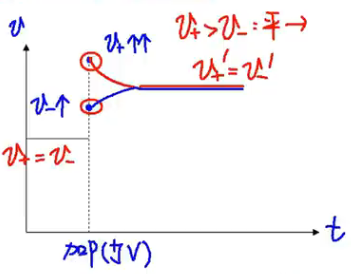
   浓度 - 时间图：

   

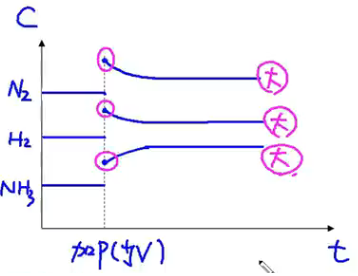
   【减压（增大容器体积）】

   反应速率 - 时间图：

   

   浓度 - 时间图：

   

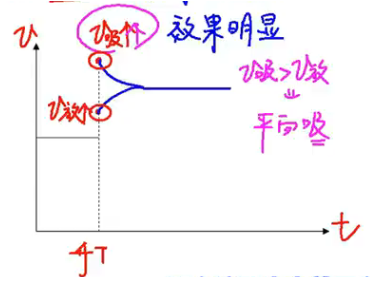
3. 温度效应：\(\ce{N2(g) + 3H2(g) <=> 2NH3(g)}~~~\pu{\Delta H = -91.5kJ}\)

   技巧：温度对吸热反应效果明显。

   【升温】

   结论：温度升高，平衡向吸热反应方向移动。

   

   

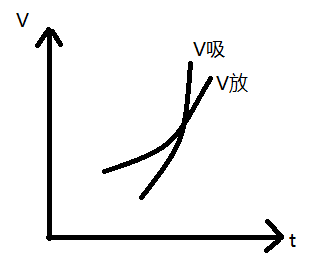
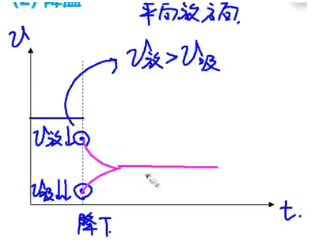
   【降温】

   结论：温度降低，平衡向着放热反应的方向移动。

   

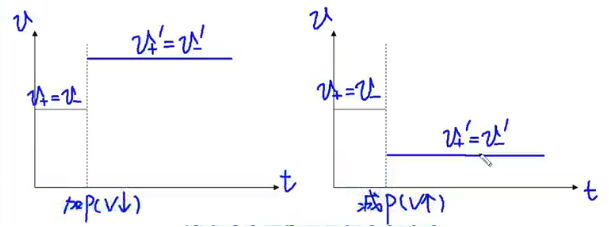
4. 平衡不移动：

   • \(\ce{H2(g) + I2(g) <=> 2HI(g)}\) 反应前后气体计量数总和相同的反应，平衡系的加压（减小容器体积）/减压（增加容器体积）不会影响化学平衡。

     

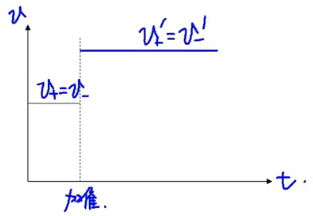
   • 平衡系加入催化剂，平衡不移动。注意：催化剂只改变反应速率，但不影响平衡。

     

等效平衡

定义

1. 定义：在一定条件下（等温等容或等温等压），对同一可逆反应体系，只是起始加入物质的情况不同（不同的投料方式），但达到化学平衡时，同种物质的百分含量（如体积分数、物质的量分数或质量分数）均相同，这样的平衡互称等效平衡。

   例如，对于反应 \(\ce{N2(g) + 3H2(g) <=> 2NH3(g)}\)，在一个容器中投入一定物质的量的 \(\ce{N2}\) 和 \(\ce{H2}\)，假设最终反应体系中 \(\ce{N2,H2,NH3}\) 的物质的量分数分别是 \(x,y,z\)，在另一个容器中投入一定物质的量的 \(\ce{NH3}\)，假设最终反应体系中 \(\ce{N2,H2,NH3}\) 的物质的量分数也是 \(x,y,z\)，那么他们的同种物质的百分含量相同，即便他们每种物质的量不相同，也是等效平衡。

   注意：等效平衡强调的是达到化学平衡时同种物质的百分含量相同，而不是同种物质的量相同。（类似于数学中的“相似三角形”。

2. 实质：化学平衡状态与条件有关，而与建立平衡的途径无关，等效平衡就是从不同的起始状态达到了相同的平衡状态。所谓不同的起始状态是指各物质的起始量不同，而相同的平衡状态是指各物质的百分含量均相同。

形成条件

1. 恒温恒容下，反应前后气体分子数改变的可逆反应，如 \(\ce{2SO2 + O2 <=>[催化剂][\Delta] 2SO3}\)。

   【等效平衡条件】

   将反应物/生成物两边中其中一边的物质，按照方程式的化学计量数转化为另一半边的物质，其反应物（或生成物）物质的量与对应组分的起始加入量完全相同，则建立的化学平衡状态是等效的。

   例如，对于上面这个方程式，如果一个容器中加入了 \(\ce{2mol SO2(g),1mol O2(g)}\)，另一个容器中加入了 \(\ce{2mol SO3(g)}\)，将 \(\ce{2mol SO3(g)}\) 按照化学计量数转化为反应物中的两种物质，即 \(\ce{2mol SO2(g),1mol O2(g)}\)，发现与前一个容器中两种物质的加入量完全相同，说明这两种容器中发生的反应是等效平衡的。

   

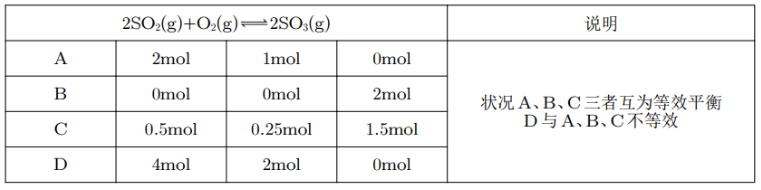
   其中，A 相当于一个 \(v~ \pu{L}\) 体积的容器里有 \(\ce{2 mol SO2 }\) 和 \(\ce{1mol O2 }\)，而 D 相当于起初一个 \(2v~\ce{L}\) 体积的容器中间有一个隔板，将整个容器分为两个 \(v~\pu{L}\) 的部分，每个部分有 \(\ce{2mol SO2 }\) 和 \(\ce{1mol O2 }\)，然后通过压缩体积使得体积与 A 中相同，那么此时在恒温恒容下，压强是 A 中的 \(2\) 倍，前后气体计量数改变，所以平衡状态改变，与 A 不互为等效平衡。此时，在 D 情况下，\(\ce{SO2}\) 的转化率 \(b\) 大于 A 情况下 \(\ce{SO2}\) 的转化率 \(a\)，D 达到平衡状态时 \(\ce{SO3}\) 的体积分数大于 A。

   【等效含义】

   各物质的物质的量（分数）、体积分数、浓度、混合气体的密度、平均摩尔质量、容器的体积，体系的压强，气体的反应速率灯所有方面均完全对应相等（类似全等三角形）。

2. 恒温恒容下，反应前后气体分子数不变的可逆反应，如：\(\ce{H2(g) + I2(g) <=> 2HI(g)}\)。

   【等效平衡条件】

   如果按化学方程式的化学计量数关系转化为方程式同一半边的物质，其反应物（或生成物）物质的量与对应组分的起始加入量比例相同，则建立的化学平衡状态时等效的。

   例如，对于上述方程式，如果一个容器中加入了 \(\ce{1 mol H2(g)}\) 和 \(\ce{1mol I2(g)}\)，另一个容器中加入了 \(\ce{2mol H2(g)}\) 和 \(\ce{2mol I2(g)}\)。那么这两个容器的反应互为等效平衡。事实上，在该反应中，只要 \(\ce{H2(g)}\) 和 \(\ce{I2(g)}\) 加入的量比例不变，无论 \(\ce{HI(g)}\) 加入多少，反应均互为等效平衡。

   

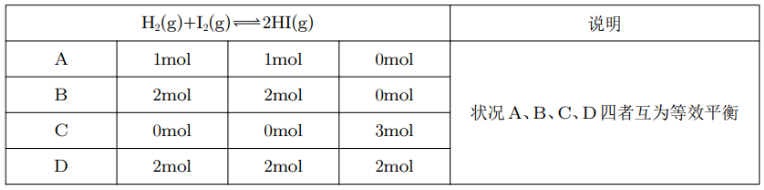
   其中，A 情况下相当于一个 \(v~\ce{L}\) 容器中加入 \(\ce{1mol H2}\) 和 \(\ce{1mol I2}\)，而 B 相当于起初一个 \(2v~\ce{L}\) 体积的容器中间有一个隔板，将整个容器分为两个 \(v~\pu{L}\) 的部分，每个部分有 \(\ce{1mol H2}\) 和 \(\ce{1mol I2 }\)，然后通过压缩体积使得体积与 A 中相同，那么此时在恒温恒容下，压强是 A 中的 \(2\) 倍，前后气体计量数不变，所以平衡状态不变。

   【等效含义】

   各物质的物质的量分数（不是物质的量）、体积分数、混合气体的平均摩尔质量、容器的体积相同；但各物质的物质的量、浓度、混合气体的浓度、体系的压强、气体的反应速率灯不相同且成比例（类似于相似三角形）。

3. 恒温恒压下的可逆反应。

   【等效平衡条件】

   如果根据反应化学方程式计量数比换算到同一半边时，只要反应物（或生成物）中各组成的物质的量比例相同，即为等效平衡。

   

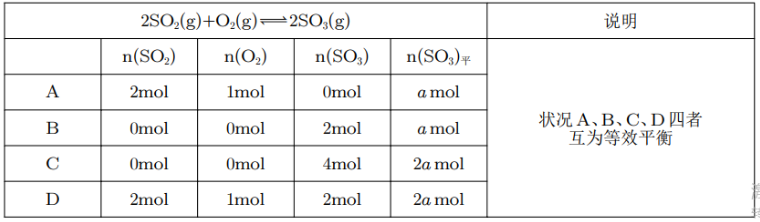
   其中，A 和 B 是投料方式完全相同的全等三角形类等效平衡。C 与 A 互为投料方式成比例的相似三角形类等效平衡。对于情况 A 和 C，相当于 C 情况的容器中 \(n(\ce{SO2})\) 和 \(n(\ce{O2})\)，以及 \(V(\ce{SO2})\) 和 \(V(\ce{O2})\) 都变为原来的两倍，所以物质的量浓度不变，那么反应平衡状态不变。

   【等效含义】

   各物质的物质的量分数、体积分数、混合气体的平均摩尔质量、浓度、混合气体的密度、体系的压强、气体的反应速率等均相同，但气体的物质的量和容器的体积不相同且成比例（类似于相似三角形）。

化学反应的方向

现代社会从环境保护 ，可持续发展，以及循环经济等方面不断地对化学家提出更高的要求。为了满足人类生存和发展的需要，化学家需要创造性地研究和设计新的化学反应。

一个化学反应在给定条件（通常指温度、压强）下能否自发进行以及在什么条件下有可能按预期的方向发生，仅用实验的方法来摸索可能要付出极大的代价，甚至会徒劳无功，因此有必要寻求一种客观的判据，用来判断一个化学反应能否正向自发进行。

自发过程与自发反应

1. 自发过程：在一定条件下，不用借助于外力就可以自动进行的过程称为自发过程。
2. 自发反应与非自发反应：
   • 自发反应：在给定的条件下，无需外力，一经引发即能自动进行的反应；
   • 非自发反应：不能自发地进行，必须借助于某种外力才能进行的反应。
3. 注意事项：
   1. 自发反应必须说明温度和压强，只有在确切的温度和压强下才能确定反应是否能自发进行。
   2. 自发反应并不是不需要任何条件就能发生，其“自发性”只强调反应是否能自动发生的可能性，并非“一定正在反应”，即表示的是一种「潜能」，而非「正在进行的状态」，类似于「重力势能」。
   3. 自发反应指的是一旦启动反应，就会自动反应，所以关键在于启动反应。
   4. 非自发反应在一定外力条件下可能发生。
   5. 自发反应与非自发反应的区别是：前者只需要一定的「条件」即可发生，而后者需要「外力」，前者的「条件」主要是指与温度和压强有关的条件，例如加热、点燃、催化剂等，而后者的「外力」必须做功，例如电解。
4. 常见的自发过程和自发反应：
   • 自然界中的水总是从高处往低处流；
   • 电流总是从电势高的地方向电势低的地方流动；
   • 室温下冰块自动融化；
   • 铁器暴露在潮湿的空气中会生锈；
   • \(\ce{Zn}\) 与 \(\ce{CuSO4}\) 溶液反应生成 \(\ce{Cu}\) 和 \(\ce{ZnSO4}\) 是自发过程，其逆反应是非自发过程。

自发反应与焓变的关系

大多数放热反应可以自发进行，但也有很多吸热反应能自发进行，因此，反应焓变是与反应进行的方向有关的因素之一，但不是决定反应能否自发进行的唯一因素。

反应熵变与反应方向

1. 混乱度及自发过程：\(\ce{H2}\) 和 \(\ce{Cl2}\) 的扩散实验如图所示。

   

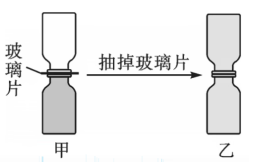
   • 实验操作及现象：如图所示，两个广口瓶中分别盛有 \(\ce{H2}\) 和 \(\ce{Cl2}\)，开始时中间用玻璃片隔开，当抽掉玻璃片后，可观察到盛放 \(\ce{Cl2}\) 的瓶内气体颜色逐渐变浅，而盛放 \(\ce{H2}\) 的瓶内显现出了浅黄绿色，最后两瓶中的颜色相同。
   • 原因解释：不需要外界的任何作用气体通过分子的扩散自发地混合均匀，体系的混乱度增加。

2. 熵（\(S\)）的概念：

   1. 定义：

      自发过程的体系趋向于由有序转变为无序，体系的混乱度增大。

      体系的混乱度常用熵来描述，熵的概念是表示体系的混乱或无序程度的物理量，其符号为 \(S\)。熵值越大，体系的混乱度越大。

   2. 影响熵大小因素：

      • 同一条件下，不同的物质熵值不同。
      • 同一物质的熵与其聚集状态及外界条件有关，如对同一物质不同状态时熵值大小为 \(S(\ce{g})>S(\ce{l})>S(\ce{s})\)。
      • 物质的量越大，分子数越多，熵值越大。

3. 熵变（\(\Delta S\)）的概念：

   1. 熵变：反应前后体系熵的变化，符号为 \(\Delta S\)。

   2. 计算：反应熵变（\(\Delta S\)）= 生成物总熵 - 反应物总熵。

   3. 常见的熵增加的过程：固体的溶解过程、气体的扩散过程、水的气化过程及墨水的扩散过程都是体系混乱度增大的过程，即熵增加的过程。

   4. 产生气体或气体物质的量增大的反应，熵变通常都是正值，为熵增加反应。例如：\(\ce{2H2O2(aq) = 2H2O(l) + O2(g)}~~~\Delta S =\pu{+57.2 J *mol-1*K-1}\)。

   5. 熵判据（熵增原理）：自发过程的体系趋向于由有序转变为无序，导致体系的熵增加，这一经验规律叫做熵增原理， 也就是判断反应进行方向的熵判据。

   6. 反应熵变（\(\Delta S\)）是与反应进行的方向有关的因素之一，但不是决定反应能否自发进行的唯一因素。如：\(\ce{2Al(S) + Fe2O3(s) = Al2O3(s) + 2Fe(s)}~~~\Delta S = \pu{-39.35 J*mol-1*K-1}\)，上述反应为熵减少的反应，但在一定条件下，该反应也能自发进行。说明“熵判据”也具有一定的局限性。

      注意：事实上，只有孤立体系（与环境既没有物质交换也没有能量交换）或绝热体系（与环境既没有物质交换也没有能量交换），自发过程才向着熵增的方向进行。

用焓变和熵变综合判断反应方向

• 焓变（\(\Delta H\)）和熵变（\(\Delta S\)）都与反应的自发性有关，却又都不能独立地作为反应自发性的依据。要判断反应进行的方向，必须综合考虑体系的焓变和熵变。

• 体系的吉布斯自由能变化（\(\Delta G,\pu{kJ/mol}\)）是由焓判据和熵判据组合成的复合判据。它不仅与 \(\Delta H、\Delta S\) 有关，还与温度 \(T\) 有关，其表达式为 \(\Delta G = \Delta H - T \Delta S\)。研究表明，在等温、等压及除了体积功以外不做其他功的条件下，其规律是：

  \[\begin{aligned} &\Delta H - T \Delta S <0 &反应正向能自发进行\\ &\Delta H - T \Delta S =0 &反应达到平衡状态\\ &\Delta H - T \Delta S >0 &反应正向不能自发进行(逆向可以自发进行)\\ \end{aligned} \]

化学反应原理图像题技巧

1. 对于一个图中两条曲线的情况：

   • 如图，对于此类图像题，箭头指向哪里就读哪边的数据。

     

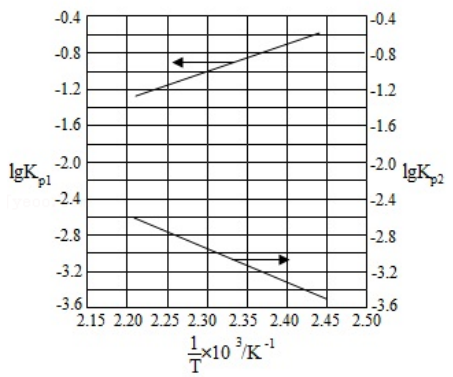
   • 对于将 \(T-x\)（温度 - 物质的量分数）和 \(P-x\)（压强 - 物质的量分数）图放在一块的图像，可以根据题目中已知的信息推断对应反应的 \(\Delta H\) 和与压强、温度有关的变化规律从而判断对应图像并求解。

2. 反应方程式相加，平衡常数 \(K\) 值相乘。

3. 求解与平衡转化率相关问题时，应该采用三段式法求解，设数时，按照比例设成具体的数比设成字母往往更方便。例如，题目中已知 \(\dfrac{n(\ce{H2})}{n(\ce{CO2})}=3\)，可设 \(n(\ce{H2})=3,n(\ce{CO2})=1\)，设为 \(3a\) 和 \(a\) 最后一定会约去 \(a\)，且容易徒增运算量。

4. 给定一个物质的量（分数）求产生的条件时，可直接读图找到对应的条件并做标记求解。

5. \(\lg K = \lg (K_{p_1}\times K_{p_2}) = \lg K_{p_1} + \lg K_{p_2}\)。

\(K_p\) 计算的解题思路

1. 概念及计算方式：对于反应 \(\ce{m A(g) + n B(g) <=> p C(g) + q D(g)}\)，其中 \(K_p=\dfrac{{P_C}^p\times {P_D}^q}{{P_A}^m \times {P_B}^n}\)，其中 \(P_A,P_B,P_C,P_D\) 均表示该气体的分压，即 \(P_分 = P_总 \times n\%\)。

   例如，\(\ce{N2 + 3H2 <=> 2NH3}\)，假设达到平衡时气体总压为 \(P_平 = \pu{6 MPa}\)，且 \(n(\ce{N2})=\pu{1mol},n(\ce{H2})=\pu{2mol},n(\ce{NH3})=\pu{3mol}\)，则 \(n_总 = \pu{6mol}\)，则 \(n(\ce{N2})\%=\dfrac{1}{6},n(\ce{H2})\% = \dfrac{2}{6},n(\ce{NH3})\% = \dfrac{3}{6}\)，所以 \(K_p=\dfrac{{P_{\ce{NH3}}}^2}{{P_{\ce{N2}}}\times {P_{\ce{H2}}}^3}\)。

2. 考察方式：

   • 直接给分压 \(P_分\)，直接根据公式计算；
   • 告诉恒温恒压，并告诉开始时的压强，需要列“四段式”，求出每个物质的量分数 \(n\%\)，然后利用 \(P_分 = P_总 \times n\%\) 计算即可。
   • 告诉恒温恒容，压强会随着反应气体计量数变化而变化，需要根据初始压强 \(P_平\) 及 \(\dfrac{P_平}{P_0}=\dfrac{n_平}{n_0}\) 计算出 \(P_平\)，然后求出 \(n\%\)，再按照上一种情况进行计算。

3. 注意事项

   • 列“四段式”计算出每个物质的量分数 \(n\%\) 后，最好通过将计算出所有物质的量分数相加看是否等于 \(1\) 来进行验算，避免计算时出现错误。
   • 按照 \(K_p\) 的计算公式计算平衡常数时，对于总压可以直接观察并计算出上下约分后剩下的总压次数，无需每次计算。
   • 对于平行反应的 \(K_p\) 计算，对应的分压带的是主副反应的总分压，而非单独主反应。求解某物质单独分压时，可设数列方程求解。

【拓】含不反应气体的 \(K_p\) 计算

1. 招法：把握不反应气体的“两不、两要、一目的”。

   • 两不：三段式中不增减、平衡常数不代入；

   • 两要：平衡总 \(n\) 要计算、平衡总压要纳入。

   • 一目的：恒温恒压条件下加入不反应气体（如稀有气体），可视为反应物压强减小，平衡向气体系数和变大方向移动，可改变平衡转化率或平衡产率。

     对比：恒温恒容条件下加入不反应气体（如稀有气体），各物质的 \(n\)、\(c\)、分压皆不变、正逆反应速率不变、平衡不移动。

2. 注意事项：

   • 列三段式时最好将不反应气体也写入三段式内，目的是为了提醒我们计算总压/总物质的量时要加入不反应气体。

【拓】等效平衡应用：恒温恒容、恒温恒压、恒温绝热

1. 恒温恒容：体系内部压强与气体物质的量成正比，气体总物质的量增大，容器总压强也增大；
2. 恒温恒压：存在可移动活塞，容器体积与气体物质的量成正比，气体总物质的量增大，容器总体积也增大；
3. 恒容绝热：容器封闭，与外界无热量交换，若 \(\Delta H <0\)，则内部放热，体系内部温度升高；若 \(\Delta H >0\)，则内部吸热，体系内部温度降低。
4. 对于反应前后气体计量数不变的反应，恒温恒容和恒温恒压条件下压强和体积相同，即两种情况下互为等效平衡，两种情况下的物质转化率也相同。
5. 判断恒容绝热与另外两种情况的关系是，可以考虑优先与恒温恒容对比，因为两者有相同变量——恒容，只有温度不相同，只需要判断温度改变时反应的方向即可。
6. 判断反应方向时，要多注意刚开始的反应是放热反应还是吸热反应（即投料方式会发生正反应还是逆反应），然后再判断温度变化。
7. 等效平衡下，正逆反应的反应物转化率 \(\alpha_正 + \alpha_逆 = 1\)。
8. 平衡常数 \(K\) 只与温度有关，只需要判断不同情况下温度的变化即可。