【题解】[ABC306G] Return to 1(数论)
【题解】[ABC306G] Return to 1
题目链接
题意概述
本题多测,\(T\) 组数据。
对于每组数据,给定一个 \(n\) 个点 \(m\) 条边的有向图,无重边自环。
问从顶点 \(1\) 出发,能否恰好走 \({10^{10}}^{100}\) 步回到 \(1\)。
数据范围
- \(1≤T,N,M≤2\times 10^5\)
- \(\sum N \le 2 \times 10^5,\sum M \le 2 \times 10^5\)
思路分析
首先,可以删掉图中无法从顶点 \(1\) 出发到达的点,和无法到达顶点 \(1\) 的点,因为无论怎么走都不可能经过这些点。那么删掉后的图是强联通的。
设 \(L\) 表示图中所有经过 \(1\) 的环长集合,\(d\) 为 \(L\) 中所有数的 \(\gcd\)。那么若从 \(1\) 出发能恰好走 \({10^{10}}^{100}\) 步回到 \(1\) 当且仅当:\(d\) 是 \({10^{10}}^{100}\) 的约数。
证明:
由于我们要从开始恰好走 \({{10}^{10}}^{100}\) 步回到 \(1\)。假设原图中有两个长度为 \(a\) 和 \(b\) 的环,那么就相当于找两个非负整数 \(x\) 和 \(y\),使得 \(ax+by=c\),其中 \(c={{10}^{10}}^{100}\)。
那么问题就转化为:对于方程 \(ax+by=c\),它有解的充要条件当且仅当 \(d|c\),其中 \(d=\gcd(a,b)\)。
充分性:根据裴蜀定理可知:存在 \(x_0,y_0\) 使得 \(ax_0+by_0=d\) ,又 \(d|c\),所以 \(c=dk=(ax_0+by_0)k=a(kx_0)+b(ky_0)\),所以方程有整数解 \((kx_0,ky_0)\);
必要性:因为 \(ax_0+by_0=c\) ,\(d\) 是 \(a,b\) 的最大公约数,所以 \(d|a,d|b\) ,所以 \(d|(ax_0+by_0)\),即 \(d|c\)。
更一般地,当原图中环的个数超过两个时,我们可以用归纳法证明出对于 \(L\) 里所有元素 \(a_1-a_n\),方程 \(a_1x_1+a_2x_2+a_3x_3+\cdots+a_nx_n=c\) 有解当且仅当 \(\gcd(a_1,a_2,\cdots,a_n)|c\)。
那么我们现在就可以有一个清晰的思路:暴力把所有的环长求出来,取它们的 \(\gcd\),判断其是否为 \({{10}^{10}}^{100}\) 的约数。
但是当经过 \(1\) 的环很多时,这种方法复杂度显然接受不了,所以考虑优化。
走到这一步,问题实际上可以转化为:
给定若干个经过 \(1\) 的环,如何求出这些环长的 \(\gcd\)?
我们考虑反向思考,首先要弄明白一个问题:对于一个数 \(x\),怎么判断它是否是所有经过 \(1\) 环长的公约数(注意这里不是最大)?
有一个方法是:从 \(1\) 开始 dfs 一遍所有点计算出每个点 \(i\) 到 \(1\) 的距离 \(dep_i\),那么要使得如果 \(x\) 是所有环长的公约数,则在 \(\bmod x\) 意义下,对于图中的每条边 \(u\rightarrow v\) 都满足 \(dep_u+1=dep_v\)。
证明:
首先考虑简单环:
- 如果给定一堆简单环,我们从 \(1\) 开始 dfs 给每个点标记一个模 \(x\) 意义下的 \(dep\),那么每个环一定都是按照一定顺序像 \(0,1,2,\cdots ,x-1,0,1,\cdots\) 这样标号的。
- 假设一个环环长为 \(len\),那么从 \(1\) 开始 dfs,到第 \(len-1\) 个点的过程中,对于非第 \(len-1\) 个点,无论如何一定有 \(dep_u+1=dep_v\),这是显然的。
- 对于第 \(len-1\) 个点当且仅当它的 \(dep\) 不是 \(x-1\) 时,这个点的编号加一模 \(x\) 不等于 \(dep_1=0\),此时 \(x\) 一定就不是该环环长的约数,与“\(x\) 是所有环长公约数”矛盾。
然后考虑复杂环:
复杂环与简单环的最主要区别就在于简单环一定不会存在公用边,也就是不会多个环经过同一条边的情况,而复杂环可能会出现。
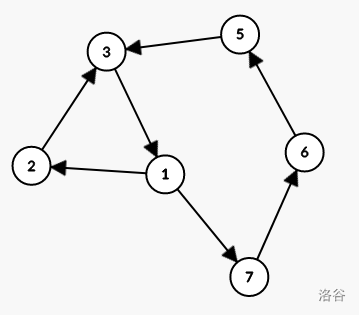
假设有两个环,环长均是 \(x\) 的约数,从 \(1\) 出发经过不同的路径到达一个点 \(u\),然后再沿着同一条从 \(u\) 到 \(1\) 路径回到 \(1\)。比如下图(两个环分别从 \(1\) 出发沿着不同路径到达 \(3\) 再沿着相同的路径从 \(3\) 回到 \(1\))。定义这个 \(u\) 为两个环的交汇点,\(len_1\)和 \(len_2\) 为两个环环长。
那么对于两个环非交汇点,同样无论如何一定有 \(dep_u+1=dep_v\)(与简单环相同)。
对于两个环交汇点 \(u\)(相当于图中的 \(3\)),如果存在其中一个环的一条边 \(v\rightarrow u\),使得模 \(x\) 意义下不满足 \(dep_v+1= dep_u\),那么当且仅当这两个环的环长差 \(|len_1-len_2|\) 不是 \(x\) 的倍数。
由于 \(x\) 是 \(len_1\) 和 \(len_2\) 的公约数,所以 \(\gcd(len_1,len_2)|x\)。根据更相减损法,有 \(\gcd(len_1,len_2)=\gcd(len_1,|len_1-len_2|)\),所以 \(\gcd(len_1,|len_1-len_2|)|x\),所以 \(|len_1-len_2|\) 一定是 \(x\) 的倍数。
由于 \(x\) 是所有环长的公约数时,在 \(\bmod x\) 意义下,对于图中的每条边 \(u\rightarrow v\) 都满足 \(dep_u+1=dep_v\),即 \(dep_u+1-dep_v\equiv 0 \pmod {x}\),所以 \(x\) 是所有 \(dep_u+1-dep_v\) 的公约数。
同理,要使得 \(x\) 是所有环长的 \(\gcd\),那么它也应该是所有 \(dep_u+1-dep_v\) 的 \(\gcd\)。
那么我们直接枚举所有边 \(u \rightarrow v\) 求出 \(dep_u+1-dep_v\) 的 \(\gcd\) 即可。
最后一步就是要判断这个 \(\gcd\) 是不是 \({{10}^{10}}^{100}\) 的约数。
由于 \({{10}^{10}}^{100}\) 只有 \(2\) 和 \(5\) 两个质因数,且 \({{10}^{10}}^{100}\) 很大,所以只需要判断 \(\gcd\) 是否只有 \(2\) 和 \(5\) 两个质因子,若是,则答案 Yes,反之是 No。
总体来说,这个题大的方面分为三步:先删掉图中无关的点;再将问题转化为求所有环长的 \(\gcd\);最后求这些环长 \(\gcd\)。
总复杂度 \(O(T\max(n,m))\)。
注意多测清空。
代码实现
//G
//The Way to The Terminal Station…
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cmath>
#define mk make_pair
#define pii pair<int,int>
using namespace std;
const int maxn=2e5+10;
int ok[maxn],dep[maxn];//ok[i] 表示 i 是否为有用点(即能不能到达 1)。
basic_string<int>edge[maxn],edge2[maxn];
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void dfs(int x)
{
ok[x]=1;
for(int y:edge2[x])
{
if(ok[y])continue;
dfs(y);
}
}
void dfs2(int x)
{
for(int y:edge[x])
{
if(!ok[y])continue;
if(dep[y]!=-1)continue;
dep[y]=dep[x]+1;
dfs2(y);
}
}
int gcd(int a,int b){if(b==0)return a;return gcd(b,a%b);}
int main()
{
int T=read();
while(T--)
{
int n,m;
n=read();m=read();
for(int i=1;i<=n;i++)edge[i].clear(),edge2[i].clear(),dep[i]=-1,ok[i]=0;
for(int i=1;i<=m;i++)
{
int u,v;
u=read();v=read();
edge[u]+=v;
edge2[v]+=u;
}
dfs(1);
dep[1]=0;
dfs2(1);
int d=0;
for(int u=1;u<=n;u++)
{
if(dep[u]==-1)continue;
for(int v:edge[u])
{
if(dep[v]==-1)continue;
d=gcd(d,abs(dep[u]+1-dep[v]));
}
}
if(!d){cout<<"No"<<'\n';continue;}//没有经过 1 的环。
while(d%2==0)d/=2;
while(d%5==0)d/=5;
if(d==1)cout<<"Yes"<<'\n';
else cout<<"No"<<"\n";
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号