【物理】磁场
前置知识
磁场中有两个现象,两个现象涵盖了磁场相关题目的主要考察范围:
电流周围有磁场,即电生磁 。
通电导线放在磁场中会受到力的作用。
对比理解电场强度与磁感应强度:
电场强度用 E B F
E = q F B = I L F
即电场强度 E q I L
这两个定义都是比值定义,即计算式 而非决定式 ,所以电场强度与 F , q B F I L
对比电场线与磁感应线:电场线是不闭合的 ,而磁感应线是闭合的 。
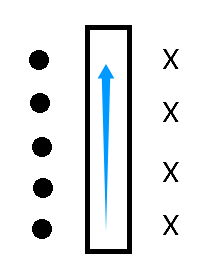
两个方向:x 表示垂直纸面向里的方向;⋅ 叉进点出 。
右手螺旋定则
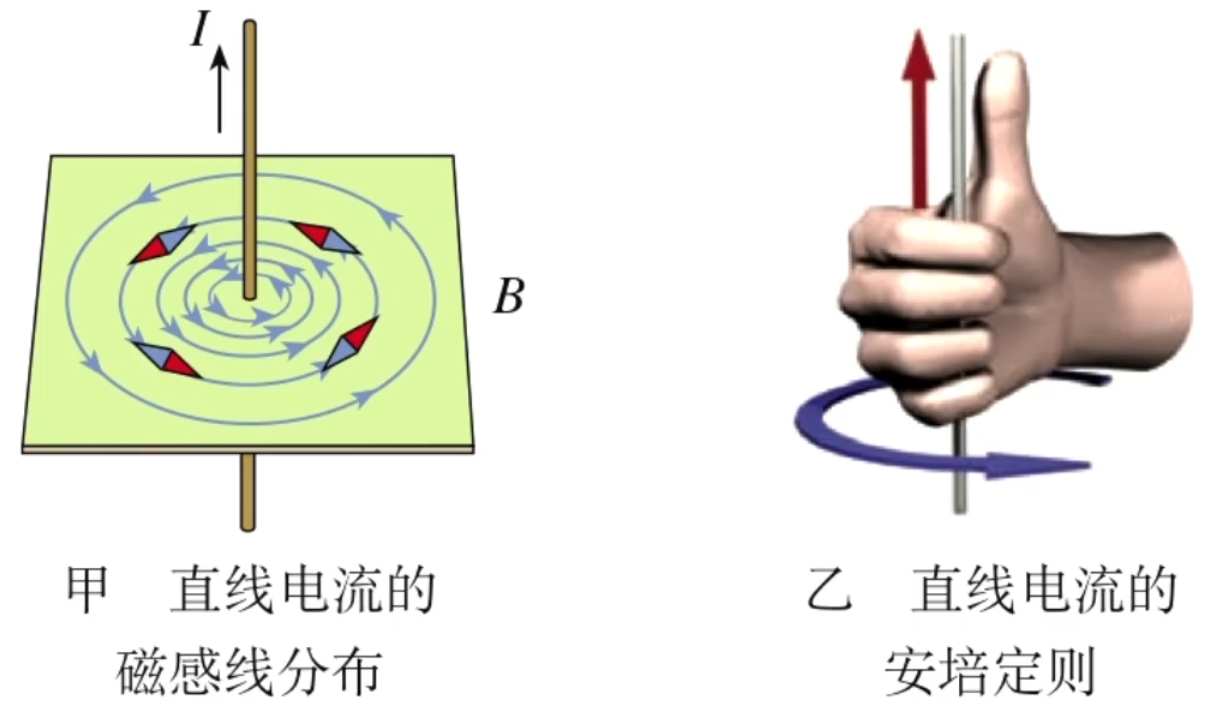
目的:确定电流周围产生磁场的方向。
直导线
方法:伸出右手,让大拇指指向电流的方向,其余四指环绕后四指方向即为磁场的方向。如下图所示。
图甲中,越靠近导线,磁场强度越强。
平面图:左边点出,右边叉进。如下图所示。
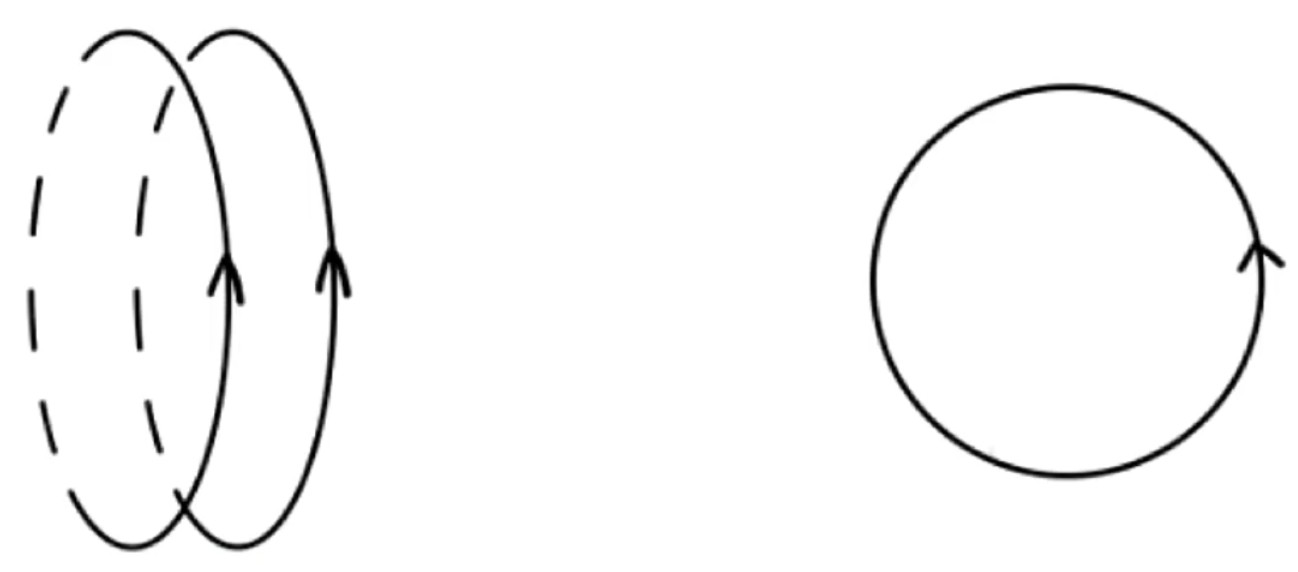
环形电流
方法:伸出右手,四指指向电流方向,则环绕后大拇指方向为磁场方向。
当环面向左 / 向右,则大拇指方向一定向左或向右,环面向前 / 向后,大拇指方向一定向前或向后,两种环面方向如下图所示。
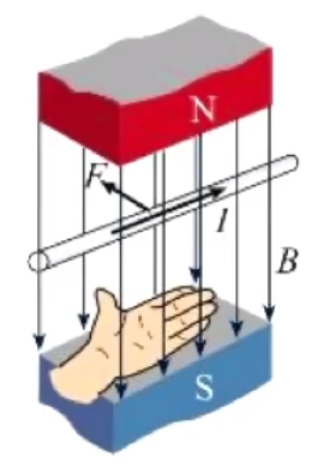
左手定则
定义通电导线放在磁场中受到的力叫做安培力 ,则这里的左手定则是为了判断安培力的方向。
步骤:
磁感线穿过掌心。
四指指向电流方向。
则拇指方向即为安培力的方向。
如下图所示。
左右手定则总结
适用范围:左力右电 ,即求力的方向是用左手定则,求电流产生磁场方向用右手定则。
安培力的方向:左手定则得到的安培力方向一定垂直于磁感线 B I 两线一点 或两线一叉 。可通过此检验安培力的方向是否画对。
通电导线周围的磁感线
小磁针旋转方向
特征:小磁针的 N
思路:画出磁感线方向,根据磁感线方向判断小磁针方向。
例题
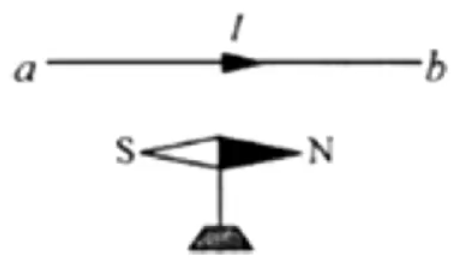
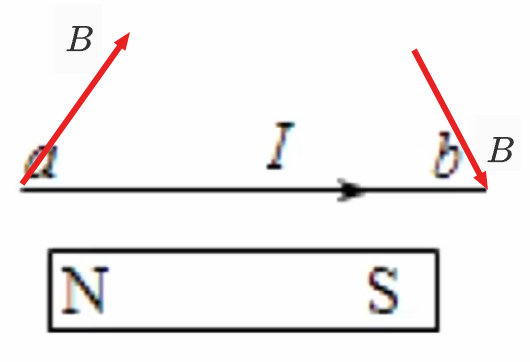
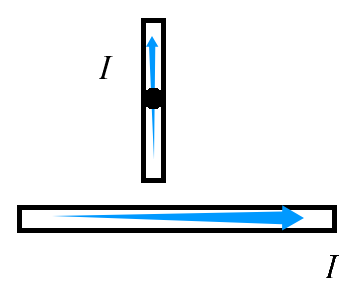
例 1:如图所示,在水平长直导线的正下方,有一只可卡因自由转动的小磁针。现给直导线通以由 a b I N
求解:
导线和小磁针垂直放置,根据右手螺旋定则可判断出直导线上点下叉 ,小磁针在直导线下面,所以 N
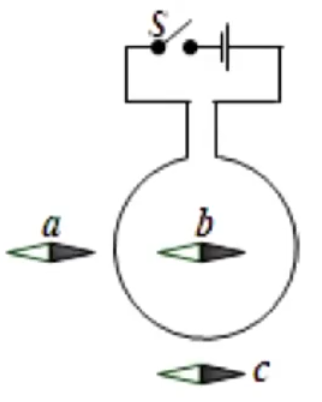
例 2:如图所示,环形导线周围有三只小磁针 a , b , c N
求解:
根据环形导线右手螺旋定则可判断出在环形导线内部,磁感线向里 ,根据磁感线是闭合的 ,那么环形导线磁感线应该是导线内部叉进,导线外部点出 (且内部叉的数量和外部点的数量相同),所以 b a , c
环形导线等效磁铁
题型:题目往往涉及一个条形磁铁和一个环形导线,需要判断在磁场的影响下环形导线如何运动。
知识:
条形磁铁磁感线从 N S
磁铁同性相斥,异性相吸。
方法:
根据右手螺旋定则判断出环形导线磁感线的方向。
根据磁感线的防线判断出环形导线等效的磁铁 N
根据磁铁 N
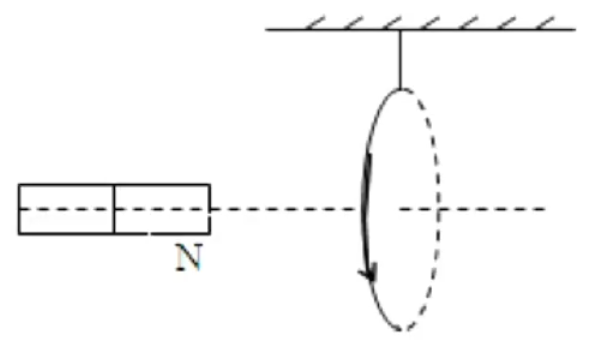
例题:如图所示,把轻质导线圈用绝缘细线悬挂在磁铁 N
求解:
根据右手定则可知环形导线的磁感线方向水平向右,那么根据条形磁铁磁感线从 N N S N
磁场叠加
知识:通电导线在某一点的磁感应强度的方向等于磁感线在该点的切线方向。
方法:
根据每个直导线的电流方向通过右手螺旋定则判断出其磁感线方向。
对每个直导线,判断出该通电导线对所求点的磁感应强度方向:可以不用画圆,磁感应强度方向一定垂直于通电导线到该点的连线(圆的切线垂直于半径),只需要根据磁感线方向判断具体方向即可。
对每个直导线的磁感应强度方向进行矢量合成。
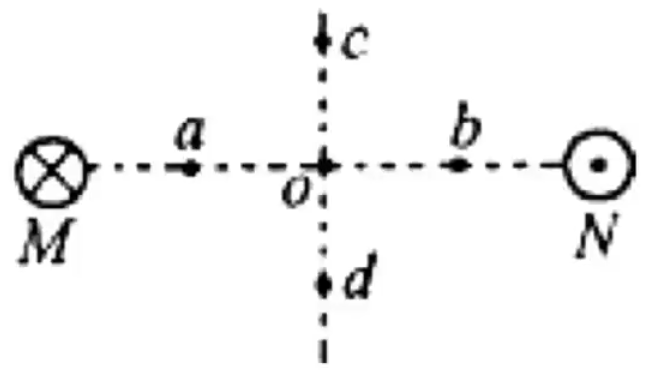
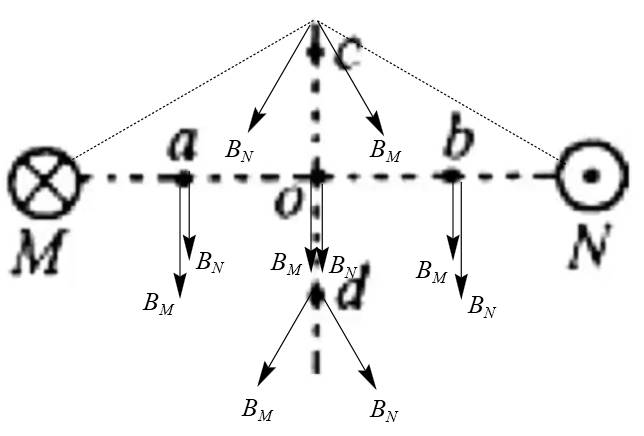
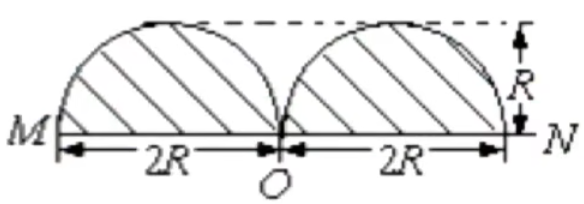
例:如图,两根平行长直导线 M N o , a , b , c , d c , o , d a o = b o = co = d o
A. o 0
B. a , c
C. a b
D. c , d
求解:
根据一点的磁感应强度方向即为磁感线在该点的切线方向可得到 M , N o , a , b , c , d
故选 B。
安培力
基础知识
安培力的计算公式:
F 安 = B I L
其中 B I L 有效长度 。
产生前提:磁感应强度 B I
注意:
公式中的磁感应强度 B I
实际上只要二者相交均可以产生安培力,只是此时需要将原来的磁感应强度 B I I
安培力 F 安 B I 但 I B 。可通过此判断安培力的大致方向。
有效长度
安培力计算公式中的有效长度 L
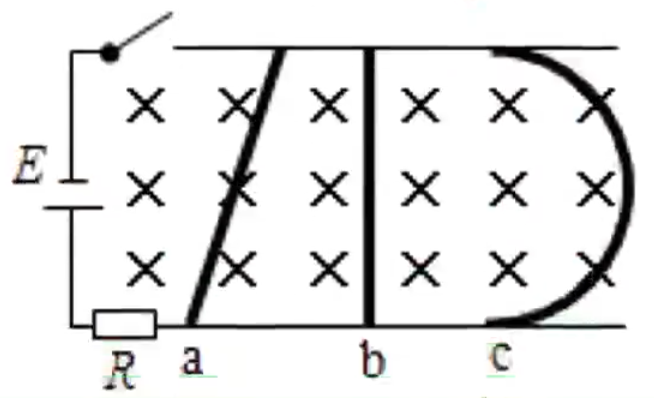
例题:如图所示,水平导轨接有电源,导轨上固定有三根用同种材料制作的导体棒 a , b , c b c b
求解:
根据有效长度的概念可知,b c L c 导体的电阻与其长度成正比 可知 R c > R b U I b > I c F 安 = B I L F b > F c
设导体的电阻与长度的关系是 R = k L k I a = R a U = k L a U I b = R b U = k L b U F a = k I a L a = k B U F b = k B U F a = F b
总结:若题目中出现「导体的电阻与其长度成正比」或「三根同种材料制成的导体」需要警惕计算安培力时电流 I
等效平面图
斜面上
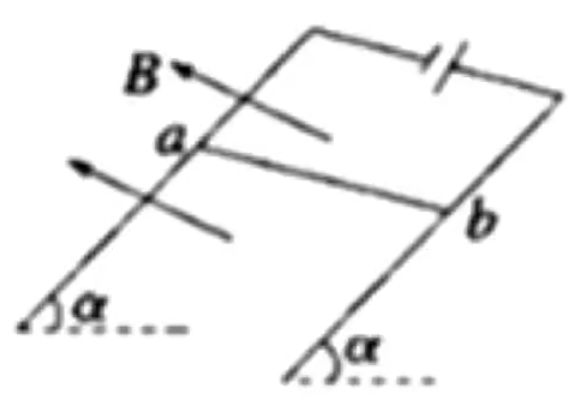
如图所示,倾角为 α ab B
其等效平面图为:
平面上
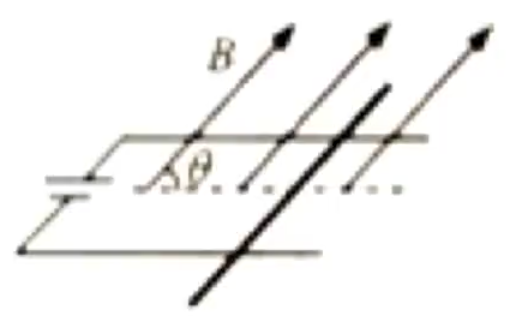
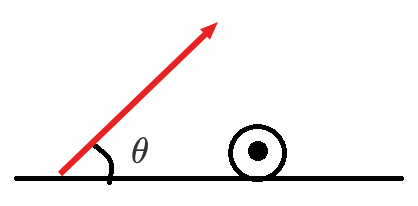
如图所示,水平金属导轨的间距为 L 2 L I B θ
其等效平面图为:
红色箭头表示 B B I F = B I ⋅ 2 L = 2 B I L
注意:这里磁感应强度 B I I B I B 如果平面图上存在一个点 / 叉和一个线,则二者代表的方向一定垂直 」。
电流间的相互作用
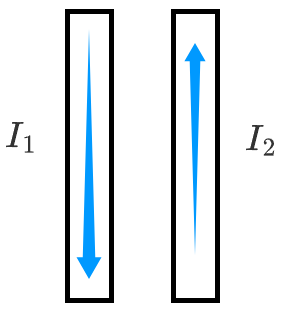
如图所示,两根通电导线平行放置,流过其中的电流分别是 I 1 I 2 I 1 I 2
那么根据右手定则可知,右导线对左导线产生的磁场向外;根据左手定则可知,左导线受到的安培力水平向左。同理,右导线受到的安培力水平向右。
当 I 1 > I 2 F = B I L B 1 < B 2 F 1 = F 2
特征:
对于电流而言,同种方向的电流相互吸引,异种方向的电流相互排斥 ,即「同向恋」。
注:一般可以通过此特征快速解题。
例:通电螺线管通电后,线圈会变短,是因为通电螺旋管处处都是方向相同的电流,会相互吸引。
流程法分析运动
步骤:
首先看题目中需要判断的是谁的运动,即确定研究对象。
判断研究对象受到谁的安培力,即施力物体。
通过右手螺旋定则分析施力物体周围的磁场,画出磁感线。
根据磁感线和导体的电流通过左手定则判断安培力的方向。
根据安培力判断物体运动方向。
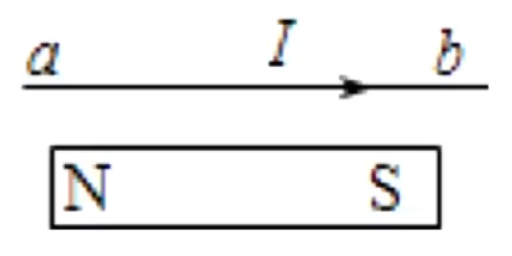
例题:如图所示,通电硬直导线 ab a b
A. a
B. a
C. a
D. a
求解:
首先,题目要求的是导线运动,那么根据题意可知导线受到条形磁铁给它的安培力,考虑画出条形磁铁形成的磁场的磁感线,即:
此时 B I B a 点出 的,导体 b 叉进 的,所以 a b
极端情况下,当 a , b 叉进 ,导线周围的磁感线水平向右,如下图所示:
根据左手定则可知,此时导体受到的安培力竖直向下,所以导体会靠近磁铁,故选 D。
说明:一般情况下绝大部分题目若问导体靠近还是远离磁铁,一般情况下都是靠近。
根据电流方向分析运动
适用范围:主要适用于两根导线的情况。
思路:直接根据「同向电流相互吸引,异向电流相互排斥」来判断运动方向或安培力方向。
例题
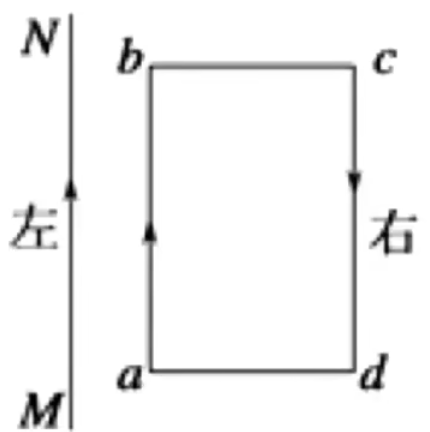
例 1:矩形通电导线框 ab c d MN ab MN MN
A. 线框有两条边不安培力
B. 线框有两条边所受安培力相同
C. 线框所受安培力的合力向左
D. 线框将绕 MN
求解:
由于「同向电流相互吸引,异向电流相互排斥」可知 MN ab c d ab MN F ab > F c d
故选 C。
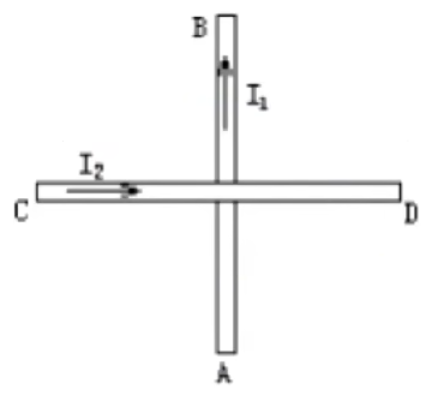
例 2:两条直导线互相垂直,如图所示,但相隔一个小距离,其中一条 A B C D C D
A. 顺时针方向转动,同时靠近导线 A B
B. 逆时针方向转动,不平动
C. 顺时针方向转动,同时离开导线 A B
D. 逆时针方向转动,同时靠近导线 A B
求解:
C D A B C D A B C D A B
特殊情况:
如下图所示,有两根导线,一根电流方向向上,,一根向右,电流向上的导线中间被一根钉子钉住,求上面的导线运动情况。
此时需要将整个导线看成两部分分析,钉子将整个导线分为两部分,其中上半部分有向右运动的趋势,下半部分也有向右运动的趋势,两个部分受到的安培力都水平向右,由于下半部分距离电流向右的导线更近,所以所受到安培力更大,那么导线整体按照下半部分的情况运动,即顺时针旋转。
注意:这里的情况与直接将导线看成一个整体分析得到的结果不同,此时不能将导线看作一个整体分析。
转换研究对象
适用范围:题目所求的研究对象直接不好分析或另一个物体作为研究对象容易分析时。
思路:转换研究对象,分析研究对象所受的安培力,然后根据牛顿第三定律推出题目所求对象所受安培力。
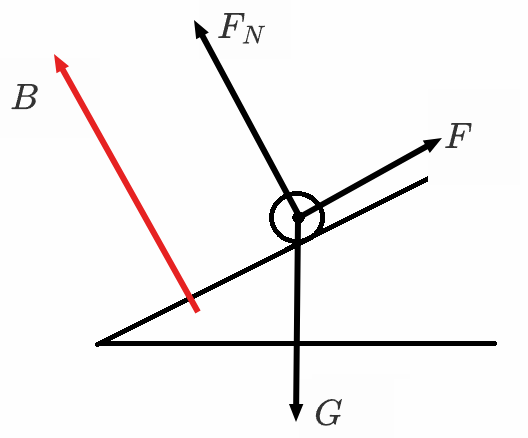
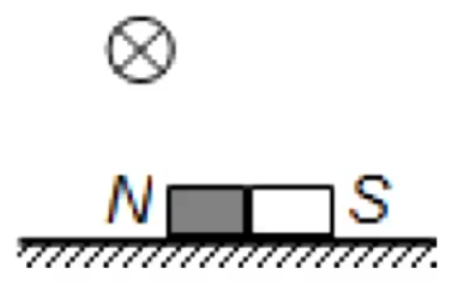
例题:如图,水平面上的条形磁铁左上方有一直导线,当导线通有垂直纸面向内的电流时,关于水平面对磁铁的支持力 N f
A. 支持力 N f
B. 支持力 N f
C. 支持力 N f
D. 支持力 N f
求解:
一般遇到条形磁铁和通电导线的题目导线更好分析,所以这里先分析导线。
根据条形磁铁周围的磁场线可知,导线上的磁感应强度方向大约斜向右上方,根据左手定则可知安培力大约斜向右下方,那么根据牛顿第三定律可知条形磁铁所受到的安培力 F N f
洛伦兹力
概念介绍
将带电粒子 在磁场中所受到的力称为洛伦兹力。
注意:洛伦兹力和安培力本质上属于同一类型的力,但二者的描述对象不同,洛伦兹力主要描述带电粒子 ,而安培力主要描述通电导线 。
公式:
f 洛 = B v q
理解记忆:类比安培力 F = B I L I = t q F = B ⋅ t q ⋅ L = B v q
推导:
⟹ ⟹ ⟹ F = B I L F = B ⋅ n es v ⋅ L n s L F = B n e f 洛 = B v q
说明:洛伦兹力相当于单位体积下每个带电粒子的安培力,所以 f 洛 = n s L F
方向:
与速度垂直。
具体方向的判断仍然使用左手定则,但与安培力的判断稍有不同:
磁感线穿掌心。
四指指向 v
拇指为 F F F
特点:永不做功 。
【题型】基础牛二与能量的结合
分析方法:与一般功能关系的问题分析方法一致,且一般情况下洛伦兹力不做功。
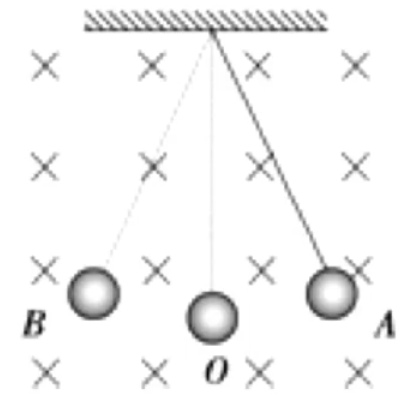
例 1(多选):如图所示,用丝线吊一个质量为 m A B O O
A. 小球的动能相同
B. 丝线所受的拉力相同
C. 小球所受的洛伦兹力相同
D. 小球向心加速度相同
求解:
A 选项:由于洛伦兹力始终与速度方向垂直,所以不做功,即整个过程只有重力做功,所以小球机械能守恒,那么两次经过 O
B 选项:当从 B O T + f 左 − m g = m r v 2 A O T − f 右 − m g = m r v 2 两次洛伦兹力大小相等方向相反 ,又根据机械能守恒可知两次速度相同,那么拉力 T
C 选项:由于两次速度方向相反,根据左手定则可知,两次洛伦兹力方向相反。C 错误。
D 选项:根据向心加速度 a = r v 2 a
故选 AD。
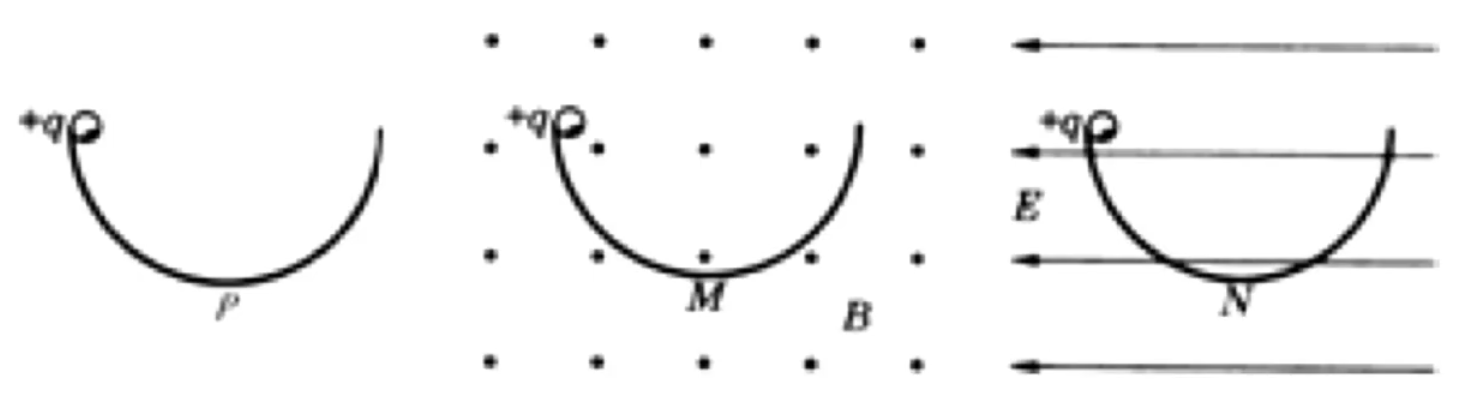
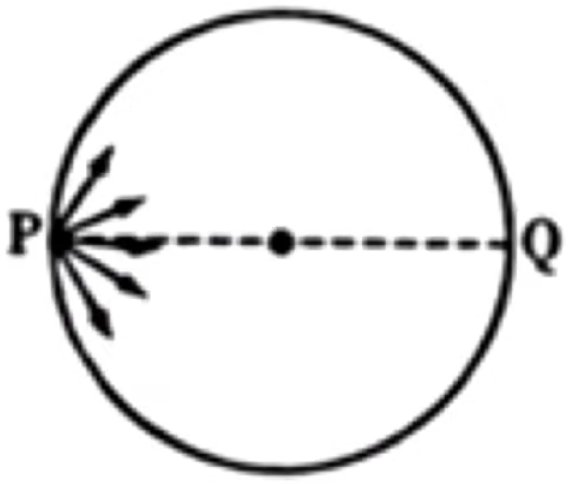
例 2(多选):如图,三个完全相同的半圆形光滑轨道竖直放置,分别处在真空、匀强磁场和匀强电场中,轨道两端在同一高度上。三个相同的带正电小球同时从轨道左端最高点由静止开始沿轨道下滑,分别通过轨道的最低点 P 、 M 、 N
A. 小球第一次到达轨道最低点的速度关系是 v P = v M > v N
B. 小球第一次到达轨道最低点时对轨道的压力关系是 F M > F P > F N
C. 小球从开始运动到第一次到达轨道最低点所用的时间关系是 t p < t M < t N
D. 三个小球到达轨道右端的高度都不相同,但都能回到原来的出发点位置
求解:
A 选项:P 、 M M v P = v M N v N < v M = v P
B 选项:对于 P F P − m g = m r v P 2 M F M − f 洛 − m g = m r v M 2 v P = v M F M > F P N F N − m g = m r v N 2 v P > v N F P > F N
C 选项:P M N
D 选项:P M N
有关洛伦兹力是否做功的问题
内容:洛伦兹力本身不做功,但其分力可能做功,洛伦兹力分力做功之和会抵消为 0
例题:一根中空的绝缘圆管放在光滑的水平桌面上。圆管底端有一个带正电的光华小球。小球的直径略小于圆管的内径。空间存在一个垂直纸面向里的匀强电场,如图所示。现用一拉力 F
A. 小球做类平抛运动,且洛伦兹力不做功
B. 小球做类平抛运动,且洛伦兹力做正功
C. 小球所受洛伦兹力一直沿圆管向管口方向
D. 小球的运动很复杂,以上说法都不对
求解:
圆管向右做匀速直线运动,那么考虑左手定则可分析得到洛伦兹力竖直向上,那么此时小球会由于洛伦兹力而产生竖直向上的加速度,那么小球整体上相对于水平桌面做水平方向上匀速直线,竖直方向上加速直线运动,那么实际运动速度应该是是方向为写向右上方的类平抛运动。
由于实际运动方向斜向右上方,那么再根据左手定则可知洛伦兹力整体上斜向左上方,所以之前根据圆管水平向右运动得到的洛伦兹力实际上是洛伦兹力的分力,此时实际运动方向与洛伦兹力方向垂直,洛伦兹力不做功。故选 A。
注意:这道题中刚开始根据圆筒向右运动从而分析得到的是洛伦兹力的分力,而非洛伦兹力,洛伦兹力一定是不做功的。
运动多情况问题
思路:对物体进行受力分析,分类讨论速度 v v − t
例题
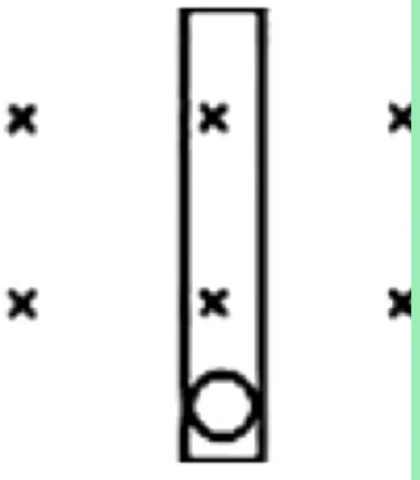
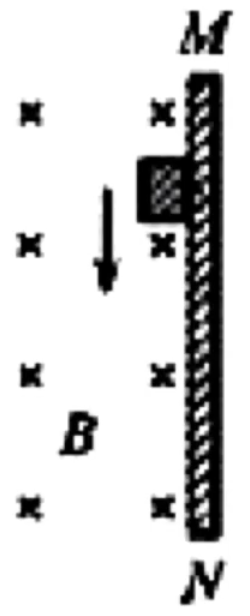
例 1(多选):如图所示,粗糙模板 MN t = 0 m q MN v − t
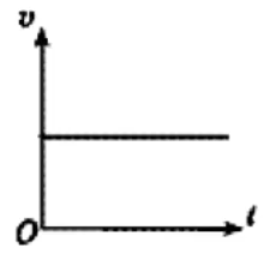
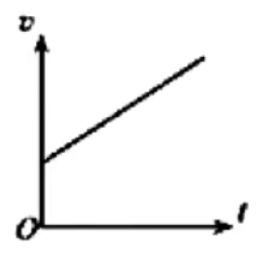
A.
B.
C.
D.
求解:
对物块受力分析有
{ F N = B v q ma = m g − μ F N
所以 ma = m g − μ B v q
当 v μ B v q > m g v a v a
当 v μ B v q < m g v a v a
当 v μ B v q = m g
故选 ACD。
例 2:如图所示为一个质量为 m + q B v 0
A.
B.
C.
D.
求解:
首先对圆环受力分析:
{ F N + B v q = m g 或 F N + m g = B v q ma = μ F N
那么当 v F N v a v F N = B v q − m g F N a
当 v F N v a v F N = m g − B v q F N a
当 v F N = m g 0
故选 B。
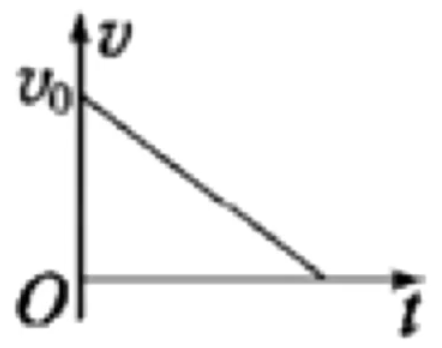
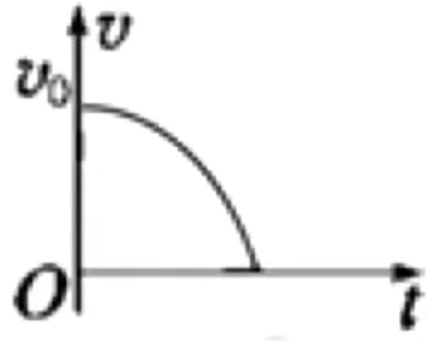
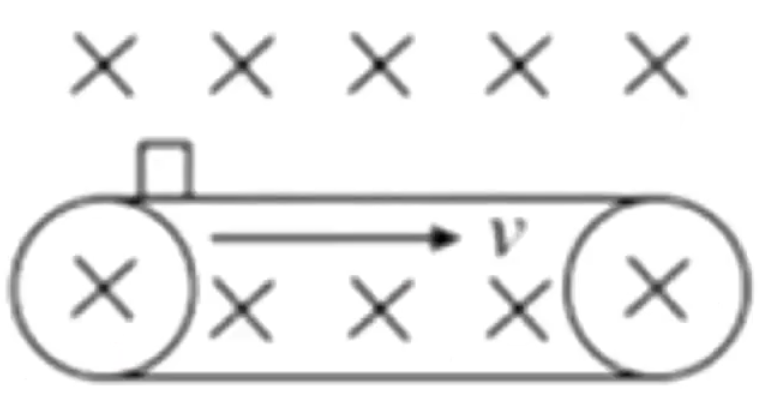
例 3:如图所示,在匀强磁场有一水平绝缘传送带以速度 v
A. 小物块先做匀加速运动,最后做匀速直线运动
B. 小物块做加速度增大的加速运动,最后脱离传送带向上做曲线运动
C. 小物块做加速度减小的加速运动,最后做匀速直线运动
D. 小物块做加速度减小的加速运动,最后脱离传送带向上做曲线运动
求解:
首先对小物块刚上传送带受力分析有:
{ F N + B v q = m g ma = μ F N
那么此时 a v v F N = m g − B v q F N a
对小物块与传送带共速后受力分析可知 μ F N = 0 F N = 0 B v q = m g
故选 C。
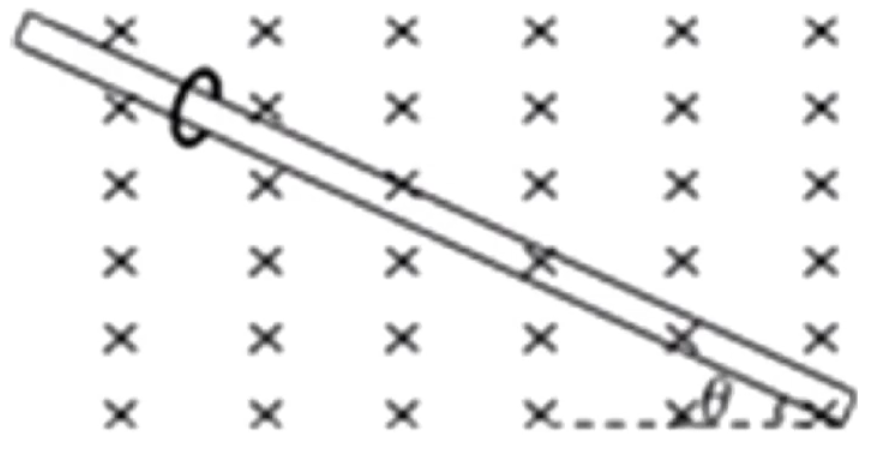
例 4:一质量 m − q θ B v 0 v 0
A.
B.
C.
D.
求解:
当首先,对圆环受力分析:
{ ma = m g sin θ + μ F N F N + B v q = m g cos θ 或 F N + m g cos θ = B v q
因为加速度 a v
当 v 0 B v q = m g cos θ F N = 0 a = g sin θ v v f 洛 = B v q m g cos θ > B v q ma = m g sin θ + μ ( m g cos θ − B v q ) v a
当 v 0 B v q > m g cos θ F N = B v q − m g cos θ v ma = m g sin θ + μ ( B v q − m g cos θ ) v a F N = 0 B v q = m g cos θ v 0 加速度减小的减速运动 再做加速度增大的减速运动 。当速度减小为 0
圆环所受到的重力 G F N f
G x > f m g cos θ + B v q = F N ma = m g sin θ − μ F N a v v F N a 做加速度减小的加速运动 。当摩擦力增大到 f = m g sin θ a = 0
所以 ABD 符合题意,故选 C。
磁场圆周
现象:若带电粒子在磁场中只受到洛伦兹力,则它一定做匀速圆周运动。
解释:洛伦兹力与速度方向垂直,所以洛伦兹力提供了向心力,导致带电粒子做圆周运动。
原理:f 洛 = F 向
三种公式
半径公式
根据 f 洛 = F 向
⟹ B v q = m r v 2 r = qB m v
即为半径公式 。
周期公式
转一圈所用的时间,即
T = v 2 π R = qB 2 πm
注意:根据公式可知,T v
时间公式
t = 36 0 ∘ θ ⋅ T
注意:这三个公式考试时不能直接使用,需要先写出 f 洛 = F 向
例题
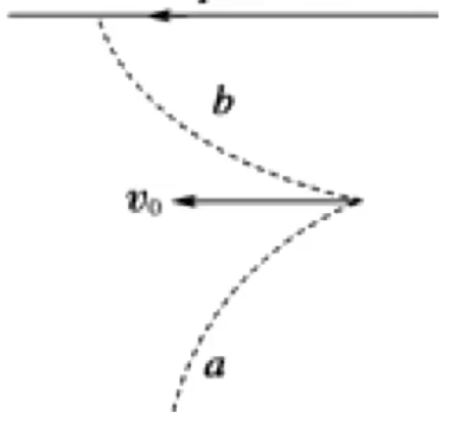
例 1:某种高速带电粒子流,具有较强的穿透能力。如图虚线为该粒子流在气泡室中穿透一张黑纸的粒子径迹照片,气泡室里有垂直纸面的匀强磁场,不计粒子重力及粒子间相互作用,下列说法正确的是()
A. 磁场方向一定垂直纸面向里
B. 磁场方向一定垂直纸面向外
C. 粒子一定从左向右穿越黑纸
D. 粒子一定从右向左穿越黑纸
求解:
由于题目没有告诉粒子正负,所以无法判断磁场方向。
根据动量 相关知识可知,粒子穿过黑纸速度会减小 ,那么由于黑纸左边半径大于右边半径,根据 r = qB m v
注意:关键是要发现「粒子穿过黑纸速度会减小」。
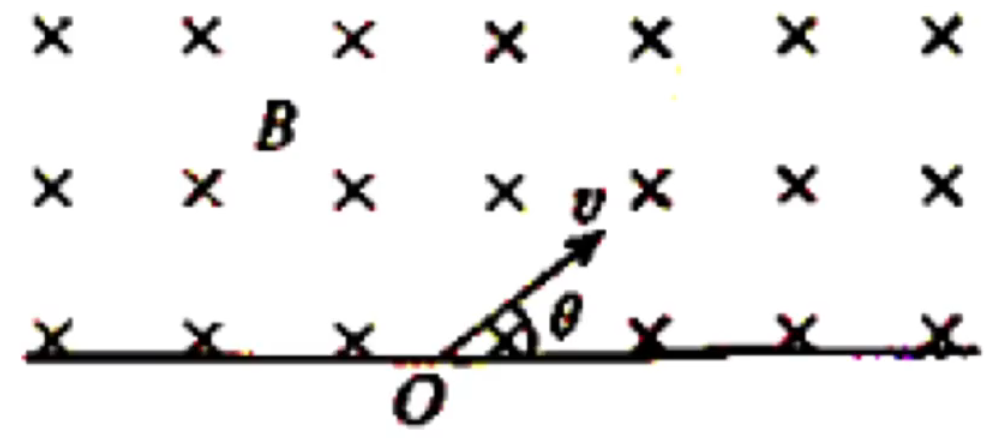
例 2:如图所示,一水平导线通以电流 I
A. 沿路径 a
B. 沿路径 a
C. 沿路径 b
D. 沿路径 b
求解:
根据左手定则 + 电子呈负电可知电子所受洛伦兹力竖直向下,所以沿路径 a R = qB m v B R
注意:这里由于洛伦兹力不做功,速度 v
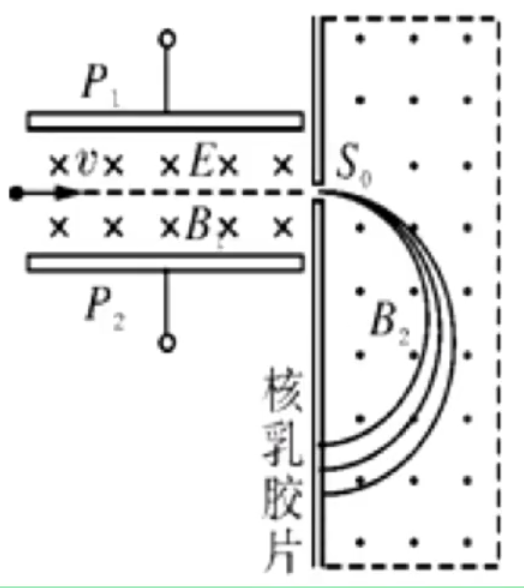
例 3:如图为质谱仪的原理图,若同一束粒子沿极板 P 1 、 P 2 S 0 B 2
A. 速度选择器的 P 1
B. 该束带电粒子带正电
C. 在 B 2
D. 在 B 2 m q
求解:
对该束带电粒子在 B 2
图示左侧两极板构成的装置的作用是「筛选速度」,一般情况下带电粒子在两极板间受到洛伦兹力和电场力,且二者方向相反,那么当洛伦兹力与电场力大小不相等(速度过大或过小),粒子均会由于有向上或向下的加速度从而撞击到两极板上,当速度恰好满足洛伦兹力等于电场力时,粒子以速度 v S 0 S 0
那么由于带电粒子带正电,所以带电粒子在两极板间所受到的洛伦兹力竖直向上,所以其受到的电场力竖直向下,所以 P 1 P 2
射入小孔 S 0 B 2
根据 R = qB m v B 2 B v q m m q
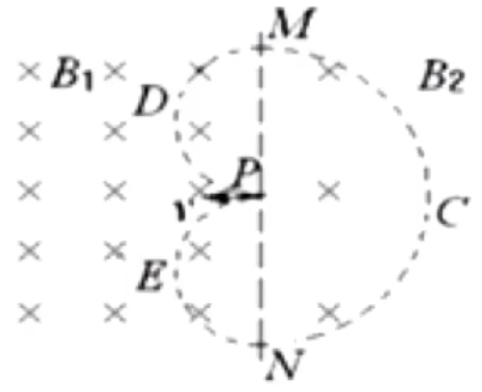
例 4(多选):如图所示,两匀强磁场的方向相同,以虚线 MN B 1 、 B 2 m e MN P B 1
A. 电子的运行轨迹为 P D MCNEP
B. 电子运行一周回到 P T = B 2 e 2 πm
C. B 1 = 2 B 2
D. B 1 = 4 B 2
求解:
对电子利用左手定则可知,其所受洛伦兹力方向竖直向上,那么运行轨迹是 P D MCNEP
电子运行一周回到 P t = T 1 + 2 1 T 2 = q B 1 2 πm + 2 1 ⋅ q B 2 2 πm
由于两电场中 R 2 R 1 = 2 1 v 1 = v 2 R = qB m v B 2 B 1 = 1 2
带入到时间表达式中可知 t = B 2 e 2 πm
故选 ABC。
注意:这里定量判断 B 1 B 2
三个几何关系
入射角 = 出射角
特征:入射角和出射角关于两点连线对称 。
这里的两点指的是入射点和出射点。
求出射角:
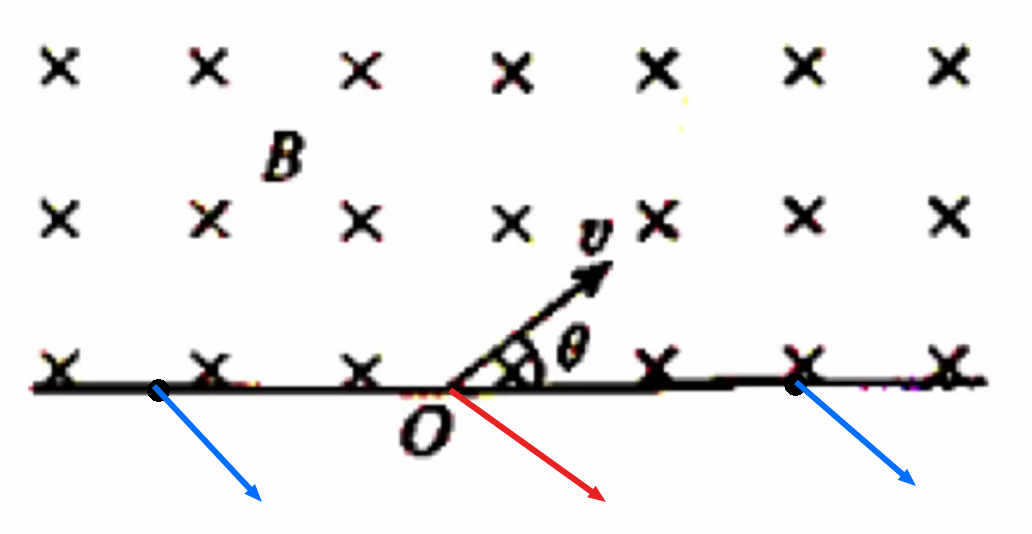
如下图所示,若下图为某带电粒子的入射方向,尝试画出其出射方向。
考虑分类讨论出射点在入射点右侧和左侧的情况,根据入射角与出射角关于两点对称,可画出大致的方向,然后平移到出射点。
当出射点在右侧时,根据左手定则可知带电粒子带负电;当出射点在左侧时,带电粒子带正电。
适用范围:题目中出射方向未知。
入射 / 出射速度的垂线与轨迹圆半径垂直
由于带电粒子在电场中做圆周运动,其轨迹的切线为速度方向,半径与切线垂直 ,所以其轨迹所在圆的半径与速度方向垂直,所以可以画出入射和出射速度方向的垂线来确定圆心的位置。
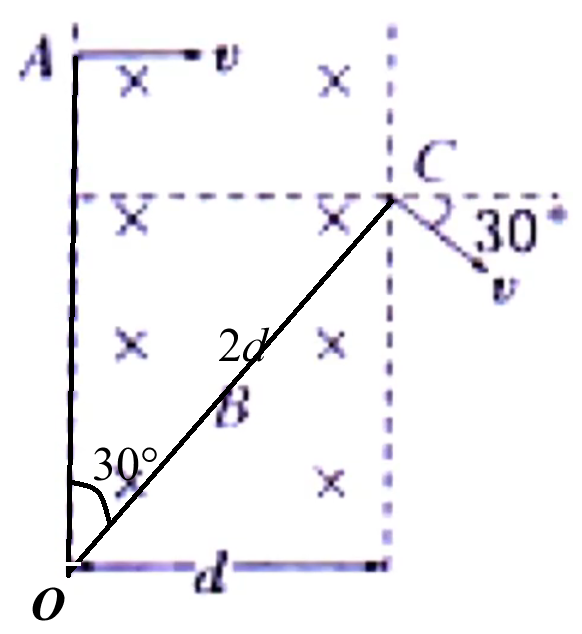
如下图所示,则点 O 3 0 ∘ 2 d
速度偏转角 = 圆心角
【速度偏转角】
以「入射角 = 出射角」中求出射角的例子为例:
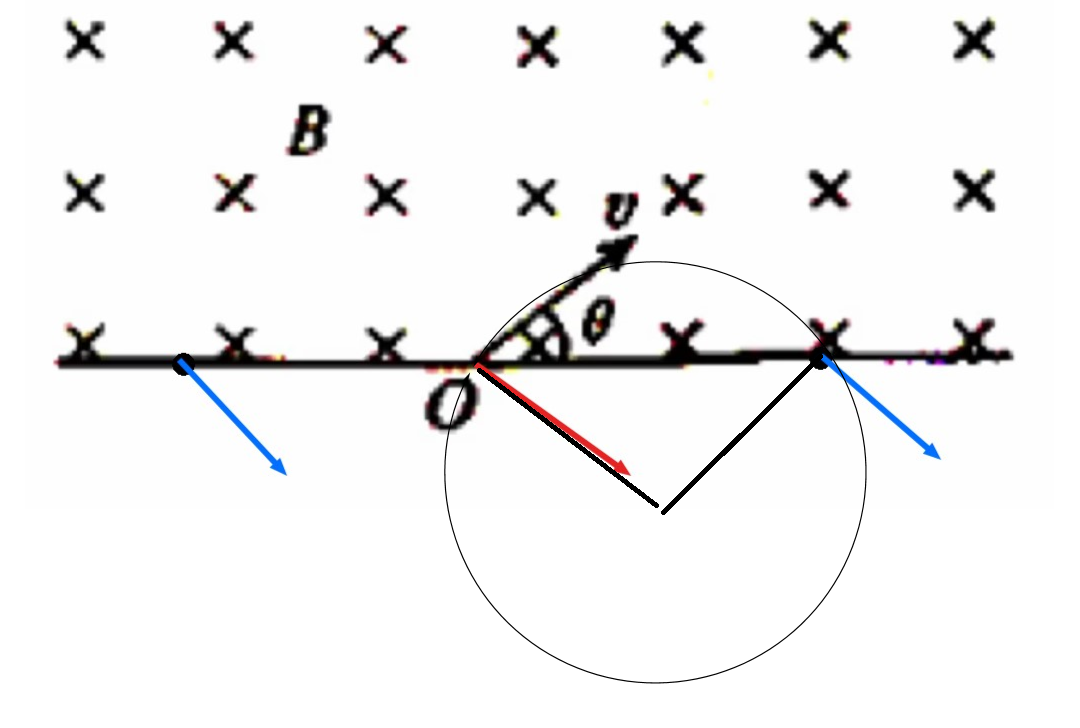
当出射点在右侧时,速度偏转角等于 2 θ 36 0 ∘ − 2 θ
【圆心角】
如下图所示,图中圆的圆心角为 2 θ
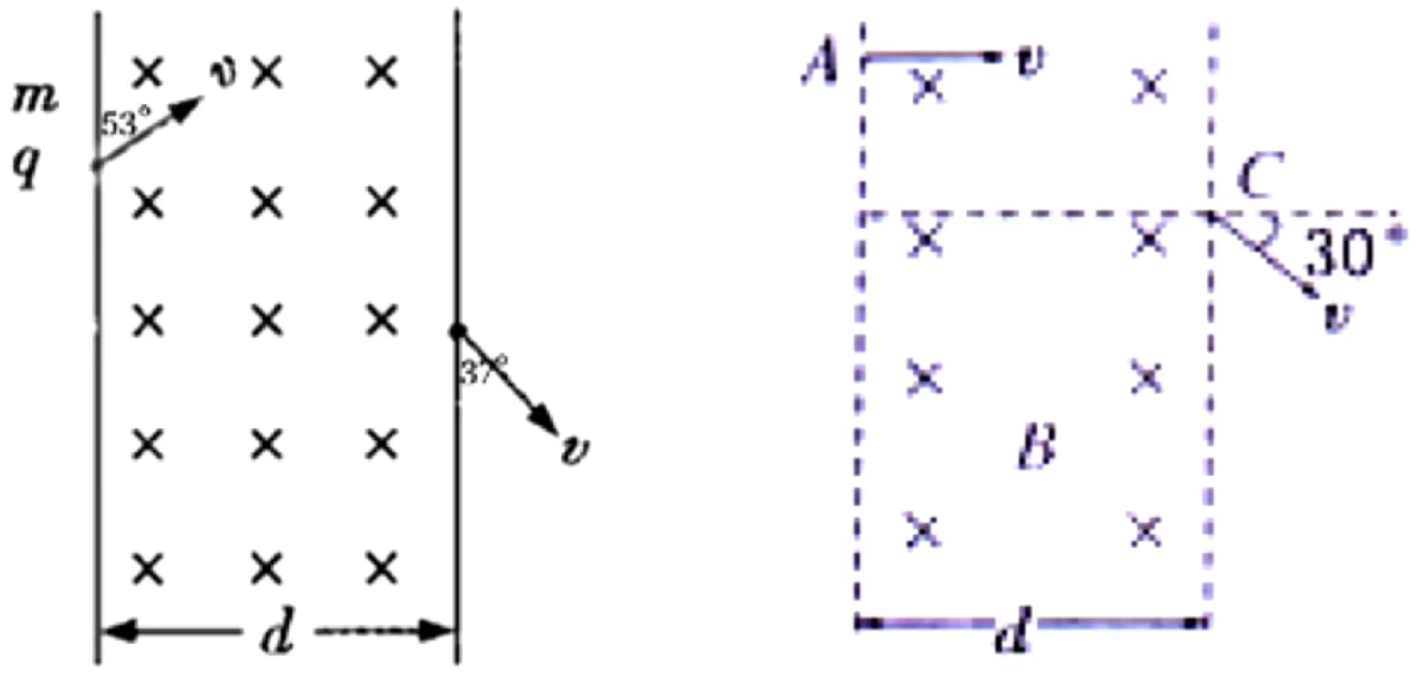
【几何关系运用】
如上图所示,左图偏转角度为 9 0 ∘ t = 4 1 ⋅ qB 2 πm 3 0 ∘ t = 12 1 ⋅ qB 2 πm
说明:一般情况下可以使用三个几何关系来解题,具体步骤如下:
若未知出射角,则先根据入射角 = 出射角画出出射角。
画出入射 / 出射速度方向的垂线,通过两垂线交点确定带电粒子运动轨迹圆的圆心。
根据速度偏转角 = 圆心角求出圆心角,并求出时间、半径等其它物理量。
注意:若题目已知同种粒子,则比荷相同,即 m q T
例题
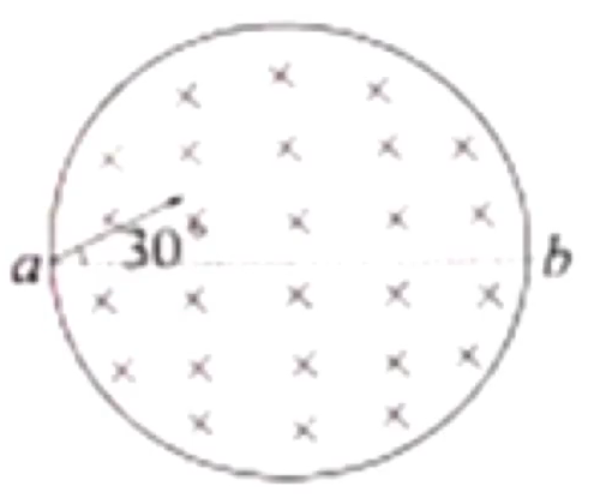
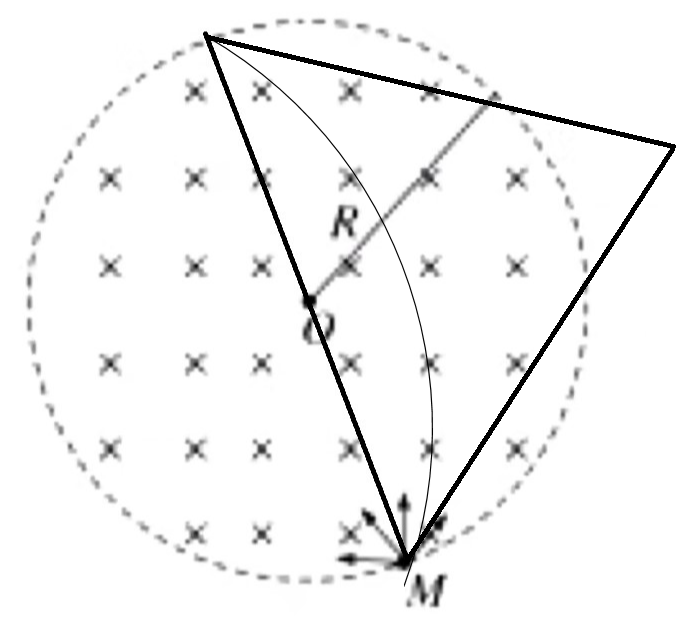
例:如图所示,在半径为 R ab B m q a v ab 3 0 ∘ b
A. 3 v 2 π R
B. v 2 π R
C. qB 2 πm
D. 6 qB πm
求解:
考虑根据入射角 = 出射角做出出射角方向,那么速度偏转角为 6 0 ∘ 6 0 ∘ t = 6 1 ⋅ qB 2 πm = 3 qB πm
画出圆心及半径,可得到轨迹圆半径 r = 2 R t = 6 1 ⋅ qB 2 π ⋅ 2 R = 3 v 2 π R
圆形磁场
特征:若一带电粒子指向圆心射入圆形磁场,则其射出方向的反向延长线一定过圆心。概括为「径向射入,一定径向射出」。
此特征往往能帮助我们较快的判断出一些选项,但具体解题时一般还是用「入射角 = 出射角」解题。
求解:一般的思路还是利用三个几何关系以及已知入射方向的一般步骤求解,只是在判断带电粒子指向圆心射入圆形磁场时出射角的方向可以利用「径向射入,一定径向射出」更快判断。
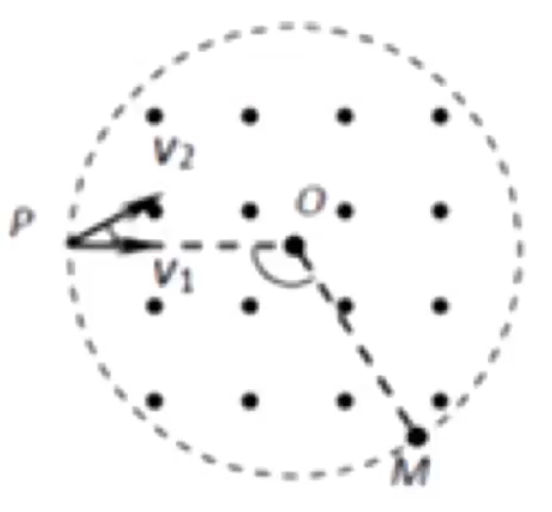
例题:如图,纸面内有一垂直于纸面向外的圆形匀强磁场区域,比荷 m q k 1 k 2 P v 1 v 2 t 1 t 2 M v 1 v 2 v 1 3 0 ∘ ∠ POM = 12 0 ∘
A. 若 v 1 = v 2 k 1 : k 2 = 3 : 1
B. 若 v 1 = v 2 t 1 : t 2 = 3 : 2
C. 若 t 1 = t 2 k 1 : k 2 = 2 : 1
D. 若 t 1 = t 2 v 1 : v 2 = 3 : 1
求解:
先根据入射角 = 出射角画出出射角,分析可知 v 1 6 0 ∘ r 1 = 3 R v 2 12 0 ∘ r 2 = R
当 v 1 = v 2
根据 R = qB m v k R k 1 : k 2 = r 2 : r 1 = 1 : 3 T = qB 2 πm T 1 : T 2 = 3 : 1 t 1 = 6 1 T 1 t 2 = 3 1 T 2 t 1 : t 2 = 3 : 2
当 t 1 = t 2
根据 t 1 = 6 1 T 1 t 2 = 3 1 T 2 T 1 : T 2 = 2 : 1 T = qB 2 πm k T k 1 : k 2 = 1 : 2 R = qB m v r 1 : r 2 = 3 : 1 v 1 : v 2 = 3 : 2
故选 B。
放缩圆
特征:已知入射方向,且入射方向方向不变 ,大小可变 。
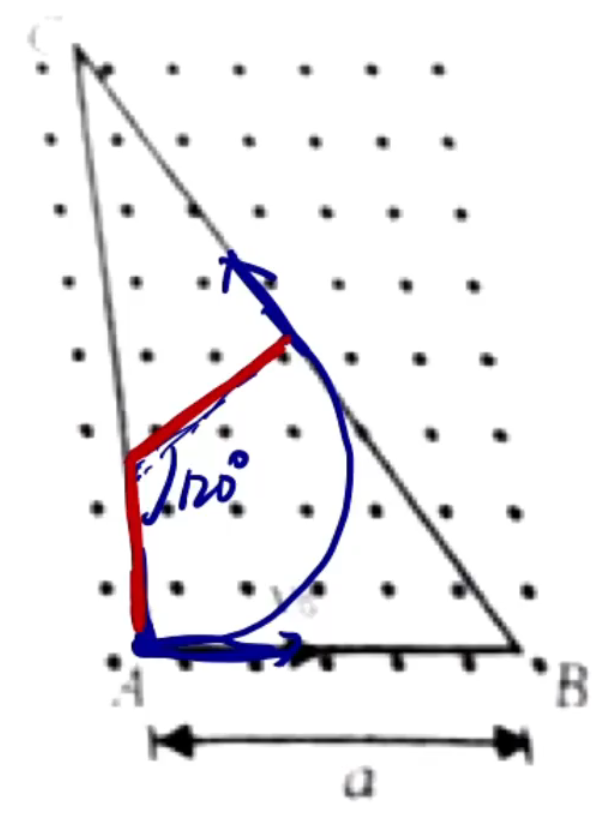
例:如图所示,在三角形区域 A C D A
A. 从 C D
B. 从 A C
C. 从 A C C
D. 从 C D C
求解:
从 A C t = 36 0 ∘ θ ⋅ T T t θ θ C
从 C D T θ C
故选 B。
总结:放缩圆的题型本质上还是已知入射方向 ,但是由于多边界的限制条件,导致不是所有粒子都能去同一条边,所以需要考虑临界状态(即轨迹圆与另一边相切)。
分析可知,当入射点和出射点在同一边(即运动回到原边)时,时间最大。例如上述例题中电子从 A C
例题
例 1:如图所示,A BC A B a ∠ A BC 6 0 ∘ m e v 0 A A B BC B
A. B > a e 3 m v 0
B. B ≤ a e 2 m v 0
C. B ≤ a e 3 m v 0
D. B > a e 2 m v 0
求解:
电子经过 BC BC BC BC 12 0 ∘
根据几何关系可知轨迹圆半径 R = 3 3 a
⟹ ⟹ R = qB m v 3 3 a = e B m v B = a e 3 m v
要使得电子经过 BC R B B B ≤ a e 3 m v 0
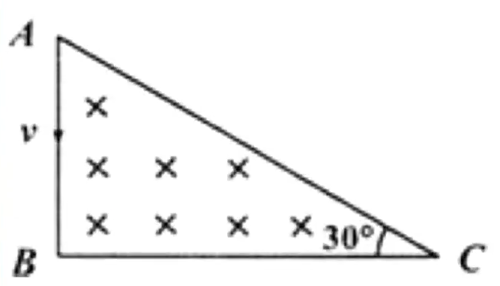
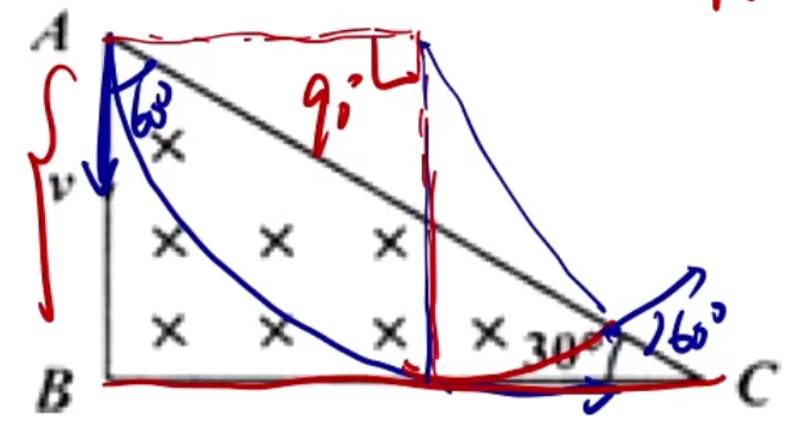
例 2:如图所示,直角三角形 A BC B A B L ∠ C = 3 0 ∘ m q A A B
求解:
当运动轨迹圆与 BC BC 9 0 ∘ R = A B = L A C 12 0 ∘ 3 1 ⋅ 2 π L = 3 2 π L
注意:这里计算最长路程时,计算的是回到 A C BC
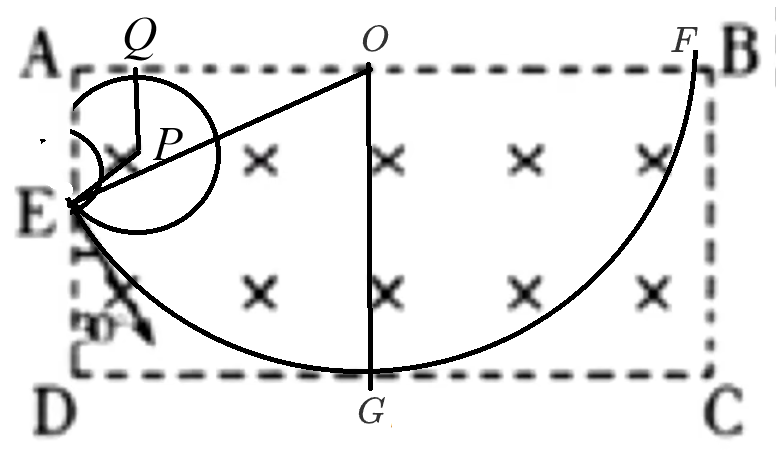
例 3:如图所示,矩阵边界 A BC D B A B 2 L A D L A D E A D 3 0 ∘ q m
A. 粒子可能从 BC
B. 经过 A B 4 m 3 qB L
C. 经过 A B m qB L
D. A B 2 L
求解:
在整个粒子运动过程中,当轨迹半径较小时,粒子会回到 A D A D A B A B D C
首先考虑如果不存在矩形边界 BC D C A B F A F < A B BC BC
那么设此时轨迹圆与 D C G E G 6 0 ∘ EG 6 0 ∘ E D = 2 1 L = 2 1 R L = R A B A F = A O + OF < 2 R = 2 L = A B BC
当轨迹圆与 A B v 240 X ∘ ∠ QPE = 12 0 ∘
2 3 R = 2 1 L ⟹ R = 3 1 L = qB m v ⟹ v = 3 m qB L
所以 B 错误。
当轨迹圆与 D C v
R = L = qB m v ⟹ v = m qB L
所以 C 正确。
由于 A Q 2 L
旋转圆
特征:已知轨迹圆大小,且大小不变,方向可变 。
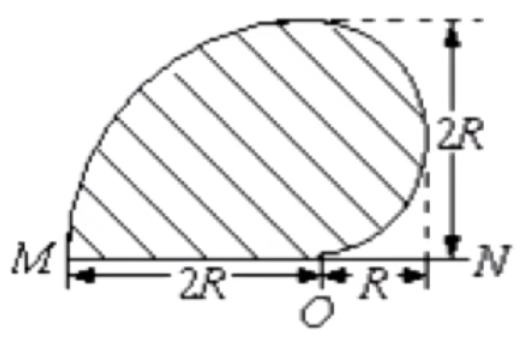
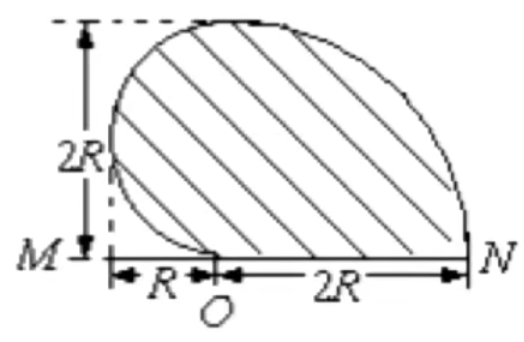
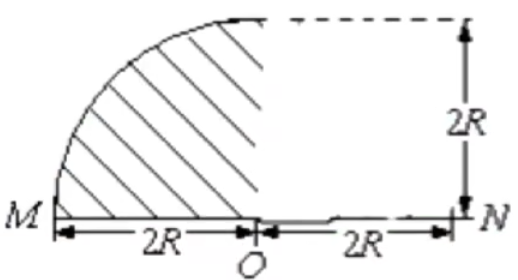
例:如图,在一水平放置的平板 MN B m + q v O R = Bq m v
A.
B.
C.
D.
求解:
首先考虑沿着 OM ON OM ON ON
考虑随着射入的电子方向逐渐向左,其所受的洛伦兹力也逐渐向左,推理可知带电粒子可能经过的区域为 A。
说明:
实际上 A 选项的右半部分是一个四分之一圆,即扇形,其半径为 2 R
根据「速度偏转角 = 圆心角」,这里沿着 ON 36 0 ∘ 18 0 ∘ 0 ∘
粒子所能达到的最远距离为 d = 2 R
总结:
求时间一般分为求整个磁场的时间 和某一边界出射的时间 。
整个磁场的最长时间:条件是要回到原边且入射角尽可能大(与另一边相切),详见下方例题中的例 1。
某一边界出射时间:主要看弦长。若 θ 圆心 < 18 0 ∘ θ θ 圆心 > 18 0 ∘ θ
说明:一般可以用「若 θ 圆心 < 18 0 ∘ θ
例题
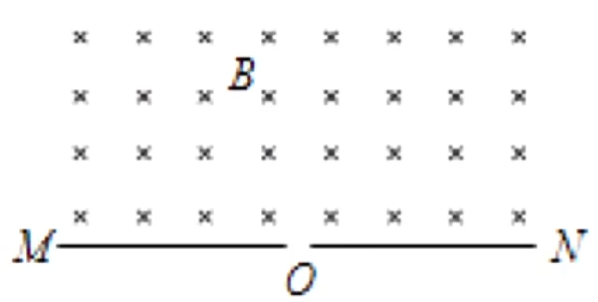
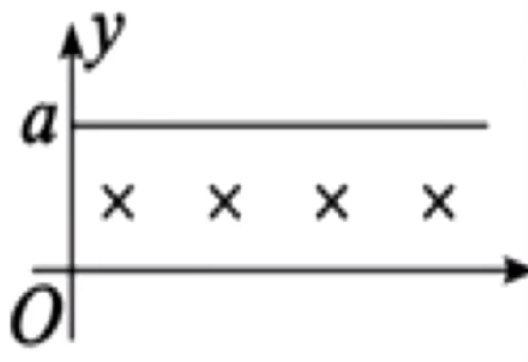
例 1:如图所示,在平面直角坐标系 x oy y ≤ a B m q O v 0 = m 2 qB a
A. 若粒子初速度沿 y 3 qB πm
B. 若粒子初速度沿 y 3 qB 2 πm
C. 粒子在磁场中运动的最长时间为 3 qB πm
D. 粒子在磁场中运动的最长时间为 3 qB 2 πm
求解:
根据 R = qB m v v 0 = m 2 qB a R = 2 a
对沿 y O R = 2 a
所以根据几何关系可知圆心角是 3 0 ∘ 12 1 ⋅ qB 2 πm = 6 pB πm
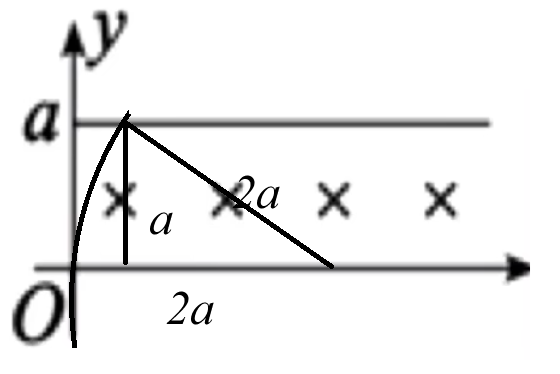
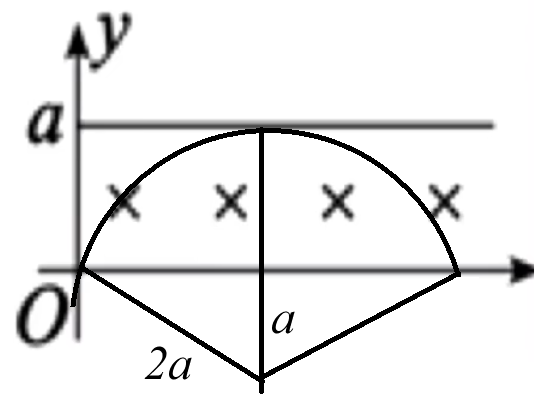
当粒子初速度方向从竖直向右到竖直向上不断改变,其速度偏转角 θ y = a y = a
此时可以根据几何关系知圆心角为 12 0 ∘ 3 1 ⋅ qB 2 πm = 3 qB 2 πm
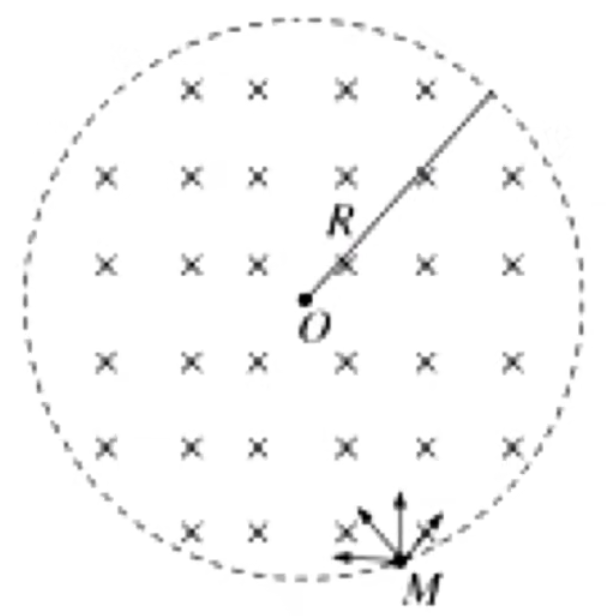
例 2:如图所示,在半径为 R B α v 0 P
A. 离子飞出磁场时的动能一定相等
B. 离子在磁场中运动的半径一定相等
C. 沿着 PQ
D. 由 Q
求解:
由于离子的速度相同,但质量不一定相同,所以动能不一定相同。A 错误。
根据 R = qB m v
沿着 PQ Q
由 P Q PQ
注意:这里题目中「一群比荷为 α v 0
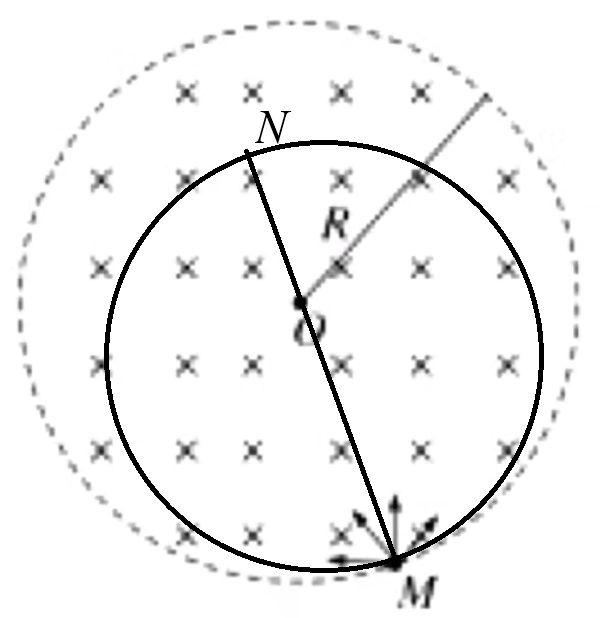
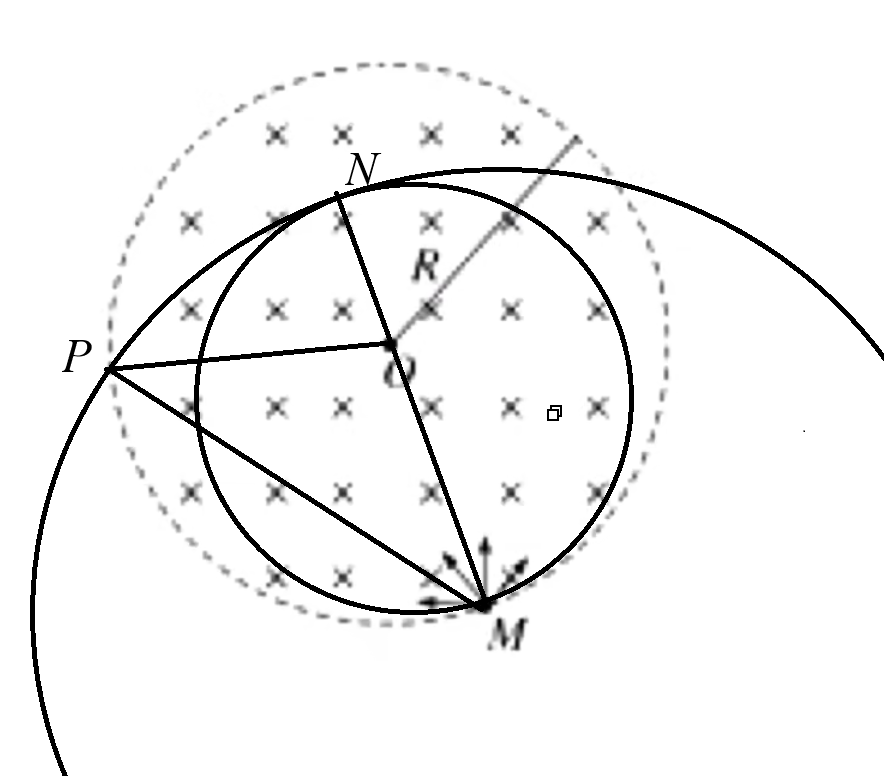
例 3:如图所示,半径为 R B M + q m M
A. 若粒子进入磁场时的速率为 v = 2 m 3 qBR 3 1
B. 若粒子进入磁场时的速率为 v = 2 m 3 qBR 2 1
C. 若粒子进入磁场时的速率为 v = m 2 qBR t = 3 qB πm
D. 若粒子进入磁场时的速率为 v = m 2 qBR t = qB πm
求解:
当 v = 2 m 3 qBR r = qB m v r = 2 3 R r < R MO MO 2 3 R
考虑将 MN M MN MN O P MP O
则 PM = 3 R OM = R ∠ POM = 12 0 ∘ PM 3 1
当 v = m 2 qBR r = 2 R r > R
所以根据几何关系可知此时圆心角为 6 0 ∘ t = 6 1 T = 6 1 ⋅ qB 2 πm = qB 3 πm
故选 AC。
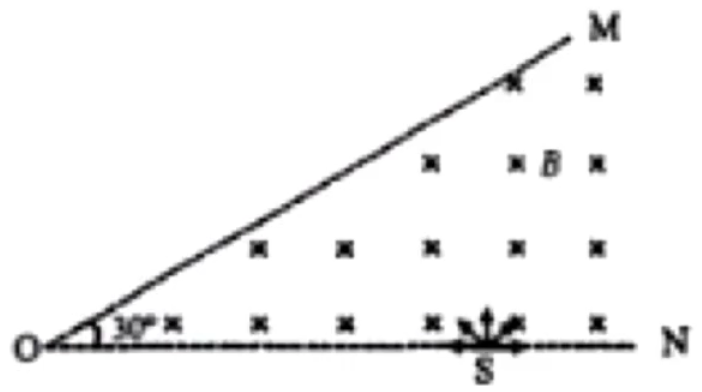
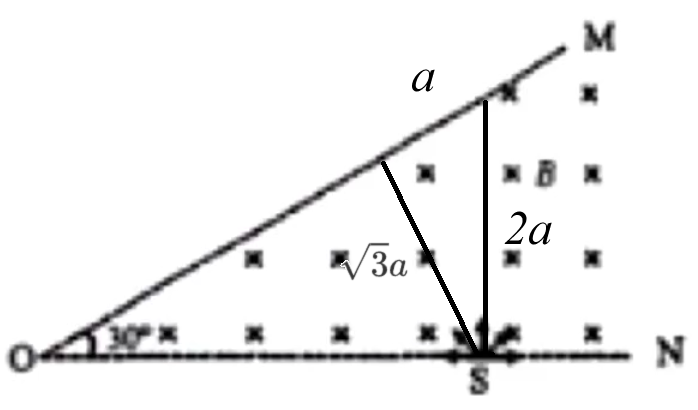
例 4:如图所示,边界 OM ON ON S S OM ∠ MON = 3 0 ∘ OM 2 1 T T OM
求解:
根据「最长时间一般发生在沿边界射入的情况下」所以沿着 SN 2 1 T 18 0 ∘ 18 0 ∘ SN θ = 9 0 ∘
所以弦长要使得时间最短,则弦长最短,那么当弦长垂直于 OM 3 a a , a , 3 a 12 0 ∘ 3 1 T
注意:这里通过弦长与入射方向的夹角与速度偏转角的关系求出了弦长与入射方向的夹角。
最小磁场面积问题
思路:
一般找入射点和出射点连起来时对应的弦长,往往这个弦长与最小面积有关,主要有两种情况:
若求的是圆形磁场 ,则一般将弦长作为直径。
若求的是矩形磁场 ,则一般将弦长作为一条边。
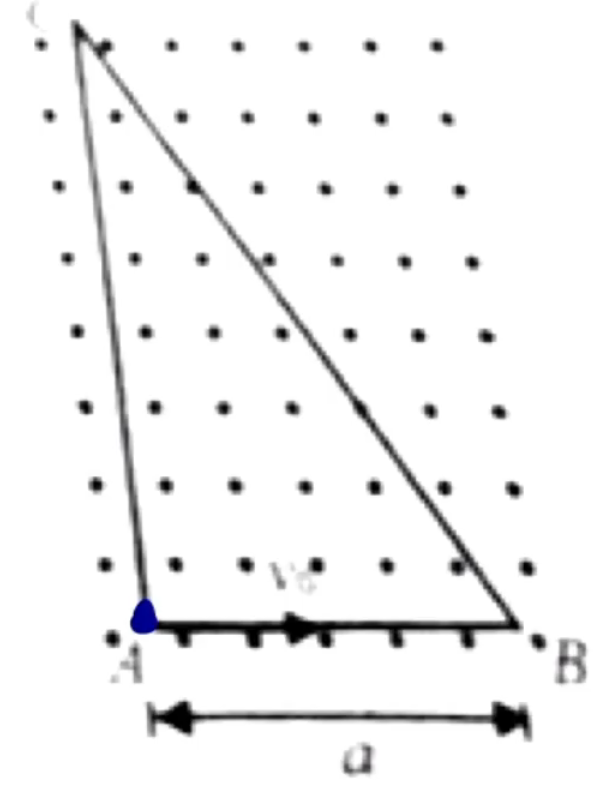
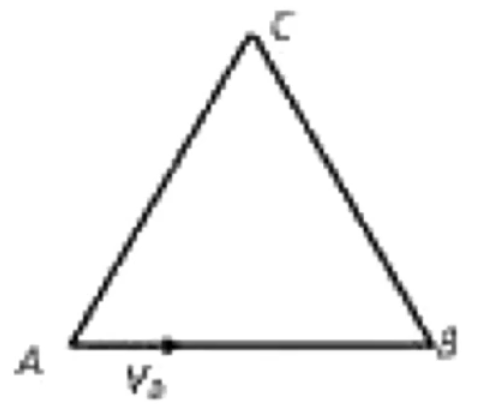
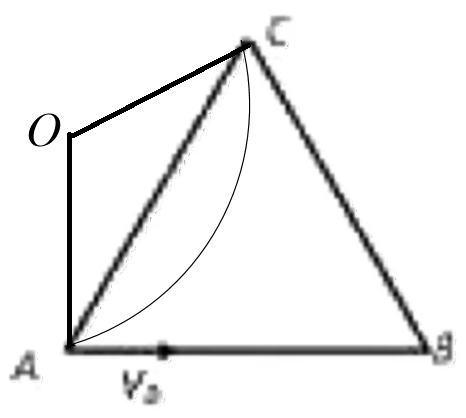
例题:一质量为 m q v 0 A A BC A B B BC
求解:
根据几何关系可画出圆心角以及运动轨迹圆。如下图所示。
则根据几何关系可知 ∠ A OC = 12 0 ∘ R = qB m v 0 A C = 3 R = qB 3 m v
要使得粒子沿着弧 A C A C A C
那么圆心磁场的最小面积 S = π r 2 = q 2 B 2 3 π m 2 v 2
拓展:若题目问求的是矩形磁场,则其最小面积为 S = A C ⋅ d = A C ⋅ 2 1 R = qB 3 m v ⋅ 2 qB m v = 2 q 2 B 2 3 m 2 v 2
地磁场
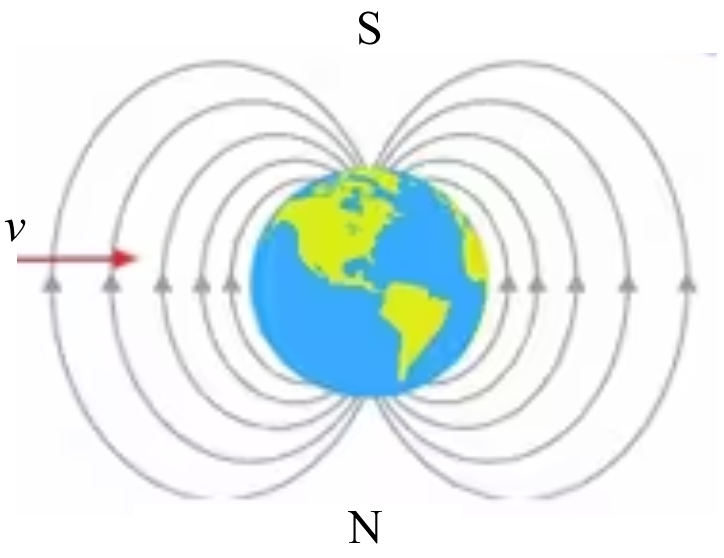
题型一:赤道上有一束自由电子,自西向东运动,那么电子会往哪偏?
求解:
可以画出赤道上方的俯视图如下。
那么根据左手定则可知电子所受到的洛伦兹力是叉进 的,所以电子会偏下运动。
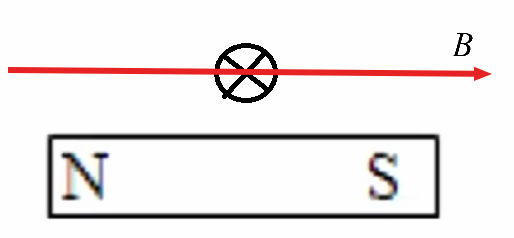
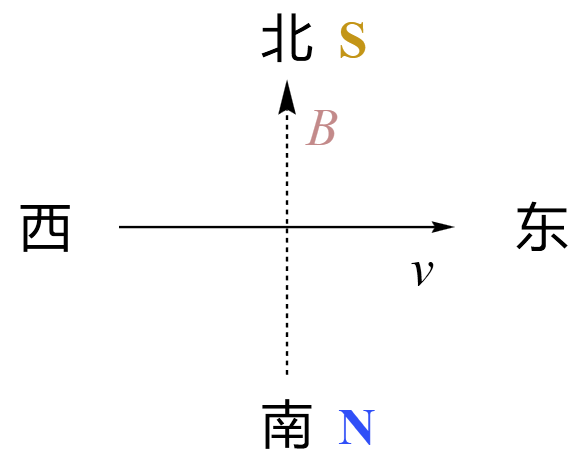
题型二:如下图所示,赤道附近的地磁场方向向北,在该处有一竖直向下运动的电子,电子所受到的地磁场的作用方向是什么?
求解:
根据左手定则可知电子受到的洛伦兹力方向垂直纸面向里,在图中相当于竖直向下。


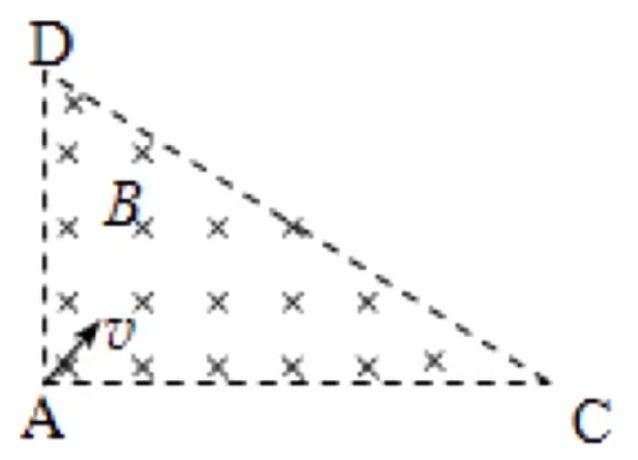





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
2022-11-11 【题解】P2260 [清华集训2012]模积和(数学,整除分块)
2022-11-11 【题解】CF1485C Floor and Mod(二分答案,整除分块)