【物理】动量

冲量

基础概念

定义

力在时间上的积累。冲量一般用字母 $I$ 表示。

公式

冲量 $I$ 的表达式如下：

由于 $F$ 的单位是 $\pu N$，$t$ 的单位是 $s$，所以冲量的单位是 $\pu{N*s}$。根据表达式可知，冲量是矢量，方向与 $F$ 相同。

注意：

• 冲量 $\ne$ 冲击力，例如自由下落的物体到达地面时，物体对地面的冲量为 $I = m \mathrm g t$，冲量是一个过程量。
• 当且仅当 $F = 0$ 时，冲量 $I = 0$。原因：冲量作为「过程量」，时间 $t$ 不能为 $0$。且一般情况下题目中只有摩擦力为 $0$ 和合外力为 $0$ 两种情况，这两种情况中，要么合外力为 $0$ 要么摩擦力不存在。所以只要有力就一定有冲量。
• 冲量的表达式为 $I = F\cdot t$，功的表达式 $W = F\cdot x \cdot \cos \theta$，二者非常相似。但功的表达式由于 $F$ 和 $x$ 都是矢量，所以存在 $\cos \theta$，而冲量不存在，是单纯的 $F$ 和 $t$ 相乘。

合冲量的计算式为

第一种计算式中 $F_合$ 一般通过牛二来求。

第二种计算式的表达式中，冲量相加为矢量相加，而非标量相加。这里与合外力做功的计算方式不同（合外力做功是标量相加），原因是冲量是矢量，而功是标量。

图像中的冲量

类比在 $F-x$ 图象中围成的面积是功 $W$，在 $F-t$ 图象中，图形围成的面积是冲量 $I$。

计算

恒力的冲量

恒力的冲量可直接用表达式 $I = F\cdot t$ 计算，注意此时要代入 $F$ 的方向计算。

变力的冲量

变力的冲量应该用合冲量的方式计算，即，将变力分解为几段，这几段内部所求力的大小和方向均不变，然后再将每一段的冲量矢量相加。

例题

例：竖直向上抛出一个物体，物体受到大小恒定的阻力 $f$，上升的时间为 $t_1$，上升的最大高度为 $h$，物体从最高点经过时间 $t_2$ 落回到抛出点。从抛出点回到抛出点的过程中，阻力做的功为 $W$，阻力的冲量为 $I_f$，重力的冲量为 $I_G$。则求问整个过程中，阻力的冲量表达式和重力冲量的表达式是什么？

分析：

定义正方向为竖直向上。

首先考虑阻力 $f$，阻力 $f$ 在整个过程中是方向改变，大小不变的变力，那么考虑分段求解。发现可以分为两段：从抛出点上升到最高点和从最高点下落到抛出点，这两段阻力的大小方向均不变，那么此时有

然后再考虑重力 $G$，重力在整个过程中是恒力，则直接根据表达式有

动量

基础概念

定义

动量指的是这个物体在它的运动方向上保持运动的趋势。一般用字母 $P$ 表示。

公式

动量 $P$ 的表达式为

即动量 $P$ 等于质量 $m$ 乘速度 $v$，单位是 $\pu{kg m/s}$。根据表达式可知，动量 $P$ 是矢量，其方向与速度方向一致。

注：

• 动能和动量都是物理中同时涉及到质量和速度的物理量，不同的是动能是标量，而动量是矢量。根据动量可以更加精准的描述物体的方向。
• 描述物体运动状态的物理量目前学过的有三个：速度、动能和动量。其中，动量是描述其状态最准确的一个，其同时涉及到质量、速度和方向。

那么对于同一质量确定的物体而言，只要速度 $v$ 改变，那么动量 $P$ 一定改变。具体来说，当速度方向改变，动量 $P$ 的方向也改变；速度大小改变，动量 $P$ 的大小也改变。注意和动能做区分：只有速度大小改变，动能 $E_k$ 才会改变；只有速度方向改变时，动能 $E_k$ 不改变。

注意：题目中「动量变化率」的概念指的是合外力 $F_合$，具体将在「动量定理」中说明。

计算

动量变化量

动量变化量 $\Delta P$ 的计算公式为

其中，$v_t$ 指的是末速度，$v_0$ 指的是初速度。

注意：该公式中 $P_末 - P_初$ 是矢量相加减，所以在最开始必须规定正方向。没有规定的情况下，默认初速度方向为正方向。同时当初速度和末速度方向在同一直线上时，可直接代入速度的数值计算；但若二者不在一条直线上，则需要通过画图计算出 $v_t - v_0$ 矢量相减的结果。

当初速度和末速度方向不在同一直线上时，动量变化量的方向为由初速度指向末速度，在平面上末速度减去初速度得到的矢量的大小即为动量变化量的大小，如下图所示，黑色有向线段的方向即为动量变化量的方向，黑色有向线段的长度即为动量变化量的大小。

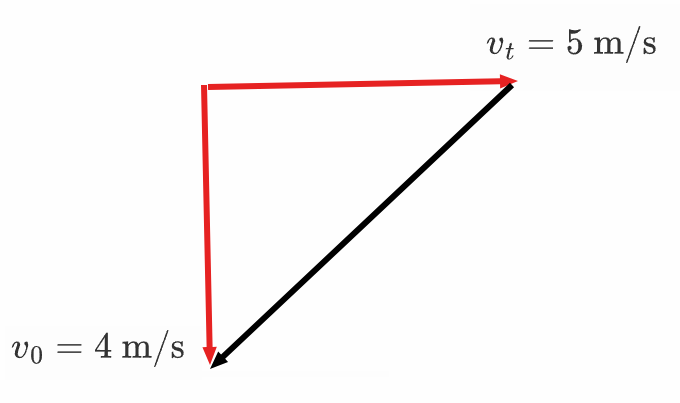
当初速度和末速度在同一直线上时，末速度减去初速度的结果得到的速度方向即为动量变化量的方向。

动量与动能的转化

已知动量 $P$，动能 $E_k$ 和质量 $m$，则

动量定理

相关概念

动量定理的表达式：

即冲量 $I$ 等于动量 $P$。

可根据牛二推导：

由于根据变化率的定义可知，动量变化率应该是 $\dfrac{\Delta P}{t}$，根据动量定理可知，动量变化率即为 $F_合$。

用动量定理解释生活中的现象：手机从空中掉入沙发和水泥地上时，速度相同，且最终速度都要变为 $0$，则 $mv_t - mv_0$ 相同，所以 $F\cdot t$ 相同，由于手机落入沙发上相比水泥地有缓冲作用，所以其落入水泥地时间更小，沙发上时间更长，所以在水泥地 $F$ 大于在沙发上的 $F$，所以手机在水泥地上更容易碎。

---

例：关于下列几种现象描述正确的是（）

A. 拳击手比赛时所带的拳套是为了增强击打效果

B. 动量相同的两个物体受相同的制动力的作用，质量小的先停下来

C. 汽车安全气囊的作用是在汽车发生剧烈碰撞时，使人更快的停下来

D. 从越高的地方跳下，落地时越危险，是因为落地时人脚受到的冲量越大

分析：

对于 A 选项，拳套是为了在动量变化量不变的情况下，增大作用时间 $t$，从而减小外力 $F$，即减弱击打效果，A 错误。

对于 B 选项，初动量相同的两个物体，由于停下来时二者末速度都是 $0$，所以末动量也相同，所以动能变化量相同；同时由于受到相同的制动力，所以 $F$ 相同，那么根据动量定理可知 $t$ 相同，所以二者同时停下来，B 错误。

对于 C 选项，安全气囊的缓冲作用是为了延长作用时间 $t$，从而减小作用力 $F$，能使人更慢的停下来，C 错误。

对于 D 选项，从越高的地方跳下，落地时 $v$ 会较大，所以初动量较大，同时由于末动量不变（都是要变为 $0$），所以动能变化量更大，即冲量更大，D 正确。

应用

动量定理的适用范围：题目中已知时间 $t$ 相关的条件。注意与动能定理的适用范围区分：当题目中出现与位移 $x$ 有关的条件时，一般使用动能定理。

利用动量定理计算动量变化量：根据动量定理 $F_合 \cdot t = m v_t - m v_0 = \Delta P$ 可知，可以通过计算出冲量来计算出动能的变化量。冲量的方向是合外力的方向，也是动量变化量的方向。

利用动量定理解题的步骤：

1. 找出研究对象。
2. 找到对应的运动段：一般涉及到两个关键点，即从哪到哪。
3. 计算出 $F_合$：对小球受力分析，求出 $F_合$，一般用正方向的力 $-$ 负方向的力。
4. 列出动量定理的式子。

解题的语言描述：对「研究对象」的「从 $A$ 到 $B$ 的运动段」列出对应的动量定理表达式。

例题

例 1：质量为 $\pu{0.2 kg}$ 的小球以 $\pu{6 m/s}$ 的速度竖直向下落至水平地面，经 $\pu{0.2 s}$ 后，再以 $\pu{4 m/s}$ 的速度反向弹回。取竖直向上为正方向，$\mathrm g = \pu{10 m/s^2}$，求：小球受到地面的平均作用力大小。

分析：

题目涉及时间 $t$，考虑动量定理。

那么对小球从落入地面到反向弹回的运动段分析，有

设小球受到地面的平均作用力大小为 $F$，对小球受力分析可知

---

例 2：质量 $m = \pu{1 kg}$ 的小球从高 $h_1 = \pu{20 m}$ 处自由下落到软垫上，反弹后上升的最大高度 $h_2 = \pu{5 m}$，小球与软垫接触的时间 $t = \pu{1 s}$，不计空气阻力，$\mathrm g = \pu{10 m/s^2}$，以竖直向下为正方向，求：接触过程中软垫对小球的平均作用力大小。

分析：

解题思路几乎与例 1 相同，可以求得动能变化量为 $\Delta P = \pu{- 30 kg m/s}$，同时根据 $F_合 \cdot t = \Delta P$ 可知，$F_合 = G - F = \pu{-30 N}$，所以小球的平均作用力 $F = \pu{40 N}$。

注意：这里的 $\pu{40 N}$ 指的是 $F$ 的大小，不包含方向，因为方向在 $F_合 = G - F$ 里已经包含了（即正方向的 $G$ 减去反方向的 $F$）。

动量守恒定律

表达式

动量守恒定律的表达式为

推导：

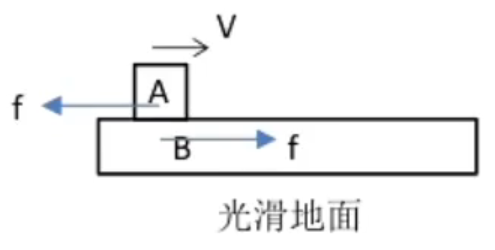
如上图所示，木板 $B$ 在光滑地面上，上表面粗糙，有一物块 $A$ 在木板上。给物块 $A$ 一个向右的初速度 $v$，物块 $A$ 做向右减速运动，物块 $B$ 做向右的加速运动，在这个过程中：

对 $A$ 和 $B$ 分别运用动量定理有

$(1) + (2)$ 得：

注意：应用动量守恒定律的表达式时，一定要规定正方向，并且速度要带着符号计算。

判定

动量守恒的判断方法

动量守恒的前提条件：系统不受外力，或系统外力矢量合为 $0$（合外力为 $0$），即 $F_合 = 0$。

衍生：

1. 若单一方向上 $F_合 = 0$，则该方向上动量守恒。
2. 内力远大于外力时，外力造成的影响可以忽略不计，可默认动量守恒。经典现象：碰撞、反弹、爆炸。

动量守恒的根本原因：系统之间相互作用力等大、反向、可以抵消。

系统动量守恒的判断：

1. 画出系统内所有物体的受力分析。
2. 抵消题目中涉及的相互作用力。
3. 判断是否水平方向上不存在任何力，即 $F_{水平}$ 是否等于 $0$。
4. 判断竖直方向上合外力矢量和是否等于 $0$，即 $F_{竖直}$ 是否等于 $0$。

常见示例

例 1：如图所示，在光滑水平面上，子弹射入木块，判断子弹射入木块的过程中，子弹和木块组成的系统是否动量守恒。

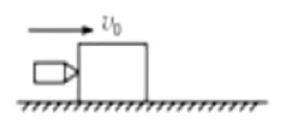
分析：子弹射入木块属于强烈撞击，此时子弹与木块的撞击力远大于外力，外力造成的影响可忽略不计，所以默认动量守恒。

例 2：如图所示，小球以一定初速度向左平抛，落在沿光滑水平面向右匀速行驶的敞篷小车上，判断小球落在车上时，小球和车组成的系统动量是否守恒。

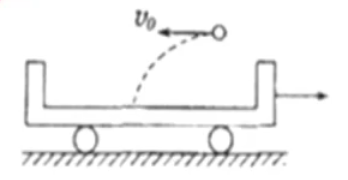
分析：同理一，小球与小车的撞击力远大于外力，外力造成的影响可忽略不急，默认动量守恒。

---

例 3：如图所示，物体沿光滑的接触面滑下，在这个过程中，判断小球和凹槽在运动过程中动量是否守恒。

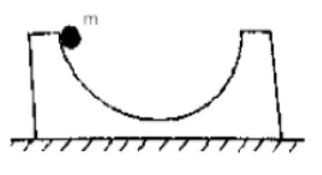
分析：

首先对小球受力分析可知小球受到重力 $G_m$ 和凹槽对它的支持力 $F_N$，对凹槽受力分析可知凹槽受到重力 $G_M$、地面对它的支持力 $F_地$ 和小球对它的弹力 ${F_N}'$，$F_N$ 和 ${F_N}'$ 是一对相互作用力，可抵消。

那么此时水平方向上不受任何力，即 $F_{水平} = 0$，所以系统在水平方向上动量守恒。

竖直方向上，凹槽相对地面静止，所以凹槽在竖直方向上平衡；小球只受到重力，所以在竖直方向上不平衡。那么整个系统在竖直方向上受力不平衡，即系统在竖直方向上动量不守恒。

例 4：如图所示，$M$ 的斜面及与地面的接触面均光滑，判断物体 $m$ 沿斜面下滑的过程中，$m$ 和 $M$ 组成的系统动量是否守恒。

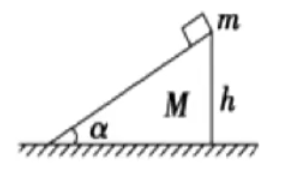
分析：同理例 3 可知，$m$ 和 $M$ 组成的系统在竖直方向上动量不守恒，水平方向上动量守恒。

注意：若 $M$ 斜面粗糙，则 $M$ 和 $m$ 有相互的摩擦力 $f$，由于此时二者摩擦力是一对相互作用力，可抵消，所以结论与例 4 的完全相同。

---

例 5：如图所示，水平面上有一斜面，其右边为固定挡板，判断木块沿光滑斜面由静止下滑的过程中，木块和斜面组成系统的动量是否守恒。

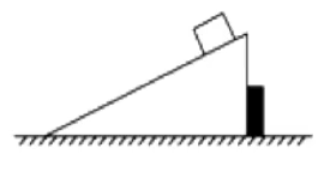
分析：

首先对小球受力分析可知，首先对小球受力分析可知小球受到重力 $G_m$ 和斜面对它的支持力 $F_N$，对斜面受力分析可知斜面受到重力 $G_M$、地面对它的支持力 $F_地$ 和小球对它的弹力 ${F_N}'$。同时由于在不考虑挡板时，斜面的合外力水平向右，所以斜面还受到挡板对其水平向左的弹力 $T$。$F_N$ 和 ${F_N}'$ 是一对相互作用力，可抵消。

那么此时水平方向上系统受到挡板对它水平向左的弹力 $T$，所以水平方向上动量不守恒。

同理例 3 可知斜面在竖直方向上动量不守恒。

---

例 6：如图所示，体积相同的两球匀速下降，细线断裂后，它们在水中运动，判断细线断裂后，木球和钢球组成的系统动量是否守恒。

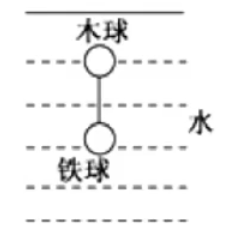
分析：

两物体在水平方向上时刻保持平衡，所以水平方向上动量一定守恒。

对于竖直方向上，首先考虑细线断裂前两球匀速运动的过程。两球匀速下降时，两球保持共速，考虑对两球整体受力分析可知：

根据 $F_浮 = G_排 = \rho_{排} \mathrm g V_{排}$ 且 $V_木 = V_铁 = V_排$ 可知，$F_{木浮} = F_{铁浮} = F_浮$。那么移项得 $F_浮 - G_木 + F_浮 - G_铁 = 0$。

那么当绳子断裂时，木球受到 $G_木$ 和 $F_浮$，铁球受到 $G_铁$ 和 $F_浮$。由于 $\rho_木 < \rho_铁$，且 $V_木 = V_铁$，所以 $G_木 < G_铁$，那么木球所受合外力竖直向上，表达式为 $F_木 = F_浮 - G_木$；铁球所受的合外力竖直向下，表达式为 $F_铁 = G_铁 - F_浮$。

那么整个系统的合外力为

所以整个系统动量守恒。

解题思路

若题目涉及的结构较为简单，或者是规则的几何图形，可直接使用「系统动量守恒的判断」中的四步法进行判断。

若题目涉及弹簧等结构或结构较为复杂，一般先对整体受力分析，水平方向上一般很好分析，竖直方向上需要考虑有无加速度。

往往判断动量守恒时，还需要判断机械能是否守恒，在此类题目中只需要判断是否存在发热即可。

注意：大部分题目涉及的系统结构都较为复杂，所以需要先对整体受力分析。

例题

例 1：如图所示的装置中，木块 $B$ 与水平桌面间的接触是光滑的，子弹 $A$ 沿水平方向射入木块后留在木块内，将弹簧压缩到最短，现将子弹、木块合弹簧合在一起作为研究对象（系统），则此系统在从子弹即将射入木块到弹簧压缩至最短的过程中（）

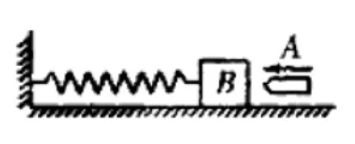
A. 动量守恒，机械能守恒

B. 动量不守恒，机械能不守恒

C. 动量守恒，机械能不守恒

D. 动量不守恒，机械能守恒

分析：

题目涉及弹簧，考虑对整个系统整体受力分析，受到重力 $G$，地面对它的支持力 $F_N$ 和墙壁对它向左的弹力 $T$，那么该系统在水平方向上受力不平衡，所以动量不守恒。

由于子弹撞击木块存在发热，所以机械能不守恒。故选 B。

---

例 2：如图所示，在光滑的水平面上有一辆平板车，人和车都处于静止状态，一个人站在车上用大锤敲打车的左端。在连续的敲打下，下列说法正确的是（）

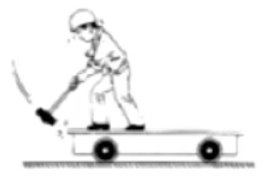
A. 车持续的向左运动

B. 车持续的向右运动

C. 大锤、人和车组成的系统动量守恒

D. 当大锤停止运动时，人和车也停止运动

分析：

本题涉及的系统结构较为复杂，考虑整体分析。对整个系统整体受力分析，受到重力 $G$，支持力 $F$，所以系统在水平方向上不受力，即水平方向上动量守恒；在竖直方向上，不能确定 $G$ 与 $F$ 的大小关系，而由于大锤在竖直方向不断由静止变为运动，所以竖直方向上存在加速度，即竖直方向上合外力不为零，动量不守恒。

由于系统在水平方向上动量守恒，所以在水平方向上列出动量守恒式为

当大锤从下到上运动时，实际上在水平方向上向左运动，那么根据上式可知车往右运动。同理，当大锤从上到下运动时，实际上在水平方向上向右运动，那么根据上式可知车往左运动。当大锤停止运动时，人和车也停止运动。

故选 D。

注意：对整体受力分析后，不能直接判断 $F$ 和 $G$ 的大小关系，需要进一步判断竖直方向上的加速度。

应用

主要公式：

题型一——基础应用

题目特征：一般情况下已知 $m_A,m_B,v_A,v_B$，并且已知 ${v_A}'$ 和 ${v_B}'$ 的其中一个，求另一个。

解法：直接代入主要公式求解。

例：一质量为 $M$ 的航天器正以速度 $v_0$ 在太空中飞行，某一时刻航天器接到加速的指令后，发动机瞬间向后喷出质量为 $m$ 的气体，气体喷出时速度大小为 $v_1$，则喷出气体后航天器的速度大小 $v_2$ 是多少？

分析：

首先题目背景属于「反冲」，一定动量守恒。那么根据动量守恒有

注意：

• 起始状态下的 $M$ 指的是后来喷出的气体 + 航天器本身为 $M$，所以计算末状态时的航天器速度，代入的航天器的质量应该是 $M - m$。
• 喷出的气体的速度方向与原航天器的方向相反，所以若规定起始时航天器的方向为正，则喷出气体的速度应该是 $- v_1$，而不是 $v_1$。

题型二——隐藏条件

题目特征：题目会隐藏一些条件，例如末状态共速。

解法：首先根据题目条件找出题目中的隐藏条件，再列动量守恒式求解。

例题

例 1：某同学质量为 $\pu{60 kg}$，再军事训练中，要求他从岸上以大小为 $\pu{2 m/s}$ 的速度跳到一条向他缓缓飘来的小船上，然后去执行任务，小船的质量是 $\pu{120 kg}$，原来的速度大小是 $\pu{0.5 m/s}$，该同学上船后又跑了几步，最终停在船上，则（）

A. 人和小船最终静止在水面上

B. 船的最终速度为 $\pu{0.5 m/s}$

C. 船的动量变化量大小为 $\pu{20 kg m/s}$

D. 该过程同学的动量变化量为 $\pu{100 kg m/s}$

---

分析：

首先由于题目整个过程属于「撞击」，所以系统动量守恒。由于末状态时「人停在船上」，所以二者最后共速，设二者共速时的速度为 $v$。

考虑对小船和人的系统运用动量守恒如下：

对于 A，由于人和小船最后以 $v = \dfrac 1 3 \pu{m/s}$ 前进，所以 A 错误。

对于 B，船最终的速度为 $\dfrac 1 3 \pu{m/s}$，B 错误。

对于 C，船的动量变化量为 $\Delta P = P_末 - P_初 = m_船 v - m_船 v_{0~船} = 120\times \dfrac 1 3 - 120 \times (-0.5) = \pu{100 kg m/s}$，C 错误。

对于 D，同理 C 的计算方式可得动量变化量为 $\pu{100 kg m/s}$，D 正确。

注意：CD 计算动量变化量时需要注意初末动量的方向，即初末速度的方向。

---

例 2：如图所示，质量为 $\pu{0.5 kg}$ 的小球在距离车底部一定高度处以初速度 $v_0 = \pu{15 m/s}$ 向左平抛，落在以 $\pu{7.5 m/s}$ 速度沿光滑水平面向右匀速行驶的敞篷小车上，车底涂有一层油泥，车与油泥的总质量为 $\pu{4 kg}$，取 $\mathrm g = \pu{10 m/s^2}$，则当小球与小车相对静止时，小车的速度大小是多少？

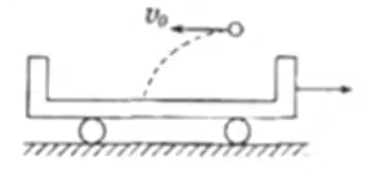
分析：

考虑对小球还未接触小车时的系统分析：

首先对小车受力分析，只受到重力；再对小车受力分析受到重力和地面对它的支持力。所以整个系统在水平方向上动量守恒，但竖直方向上，由于小车所受合外力为 $0$，而小球受到合外力等于重力，不为 $0$，所以此时系统在竖直方向上动量不守恒。

对于从小球抛出到小球与小车相对静止的整个过程中，分为两个阶段：

• 小球未落入小车上时，根据上述分析可知水平方向动量守恒，竖直方向不守恒。
• 小球落入小车上时，根据「撞击」可知动量守恒。

所以整个过程中系统动量在水平方向上守恒。

设小球相对小车静止时，二者速度为 $v$，所以根据水平方向动量守恒有：

注意：

• 此题在整个过程中只有一个方向动量守恒，而非整体动量守恒。
• 对于系统较为复杂的题目，往往不需要判断整体动量守恒，而只需要利用一个方向上动量守恒即可。

【模型】碰撞

分类

按照有无能量损失、能量损失多少分为三类：

1. 弹性碰撞：无动能损失。
2. 非弹性碰撞：有动能损失。
3. 完全非弹性碰撞：动能损失最大。

说明：

• 完全非弹性碰撞是非弹性碰撞的一种特殊情况。
• 完全非弹性碰撞中的「动能损失最大」$\ne$ 「动能全部损失」。

特点

只要是碰撞，一定动量守恒，所以一般情况下需要利用动量守恒的式子求解。

对于弹性碰撞，由于无动能损失，一般还需要利用能量守恒的式子求解。

对于非弹性碰撞，一般告诉末状态速度，做法参考「动量守恒定律 - 应用」。

对于完全非弹性碰撞，满足两小球碰撞后一定共速。因为只有两小球碰撞后达到共速时能量损失才是最大的。

对于后两种情况，题目可能会求动能损失了多少，一般根据 $E_损 = E_初 - E_末$ 求解。

弹性碰撞

一般情况

隐藏条件：

1. 动量守恒 $+$ 能量（动能）守恒。
2. 对于一后一前的两个小球 $m_1$ 和 $m_2$，二者能发生弹性碰撞当且仅当 $v_1 > v_2$，即后面小球的初速度必须大于前面小球的初速度。

特点：一般不给定两小球末状态的速度。

---

模型：

如图，已知质量 $m_1$ 的小球初速度为 $v_1$，质量 $m_2$ 的小球初速度为 $v_2$，$v_1 > v_2$，二者均向右运动，当两小球发生弹性碰撞后，二者速度分别是多少？

推导：

设两小球发生碰撞后，质量为 $m_1$ 的小球速度为 ${v_1}'$，质量为 $m_2$ 的小球速度为 ${v_2}'$。

首先根据动量守恒有：

再根据能量守恒有：

$\dfrac{(3)}{(2)}$ 得：

$(5)$ 代入 $(1)$ 得：

所以

---

题目书写过程：写出动量守恒和能量守恒的式子，然后「经化简得」「得到的两速度的结果」。

题目求解过程：直接在上述推导过程中，解由 $(1)$ 和 $(4)$ 组成二元一次的方程即可。

特殊类型弹性碰撞

注：以下三种特殊类型的前提条件均满足一般情况下的模型。

动撞静

即 $v_1 > 0,v_2 = 0$，此时有：

定义 $v_1$ 的方向为正方向。由此可以看出，质量为 $m_2$ 的小球碰撞后速度一定沿着正方向，与 $v_1$ 相同。

而质量为 $m_1$ 的小球碰撞后可以根据计算得到结果的正负判断「是否发生反弹」，有两种可能：

• 当 $m_1 > m_2$，即「重撞轻」时，计算得到结果为正，碰撞后速度与原速度方向相同，不会反弹；
• 当 $m_1 < m_2$，即「轻撞重」时，计算得到结果为负，碰撞后速度与原速度方向相反，会发生反弹。

一种特殊情况：当 $m_2$ 趋近于 $+\infty$，则 $m_1$ 可以忽略不计，根据计算结果可知 ${v_1}' \to \dfrac{-m_2 v_1}{m_2} = -v_1$，${v_2}' \to 0$。小球撞墙被反弹是这种情况的现实模型，目的是为了告诉我们小球反弹后速度大小与原速度相同，方向与原速度相反。

质量相等

当 $m_1 = m_2 = m$ 时，则根据计算结果可知 ${v_1}' = \dfrac{2m v_2}{2m} = v_2$，${v_2}' = \dfrac{2mv_1}{2m} = v_1$，即两小球速度交换。

共速法巧解弹性碰撞

假设两小球发生非完全弹性碰撞，即碰撞后共速，设两小球的速度均为 $v$，则根据动量定理有：

同时有小结论：

可求出共速时速度 $v$ 然后直接根据上述结论快速求出两小球碰撞速度。

完全非弹性碰撞

隐藏条件：

1. 动量守恒，且一般情况下已知 ${v_1}'$ 和 ${v_2}'$ 其中之一。
2. 损失的动能 $E_损 = E_初 - E_末$。
3. 末状态共速：一般情况下题目会告诉碰撞之后黏在一起，或体系内两物体不发生相对运动。

模型：

如图，已知质量 $m_1$ 的小球初速度为 $v_1$，质量 $m_2$ 的小球初速度为 $v_2$，$v_1 > v_2$，二者均向右运动，当两小球发生非完全弹性碰撞后（或两小球碰撞后共速），速度是多少？在整个过程中损失的动能是多少？

求解：

设共速时速度为 $v$。

首先根据动量守恒有

那么动量损失 $E_损$ 为

具体题目代入计算即可。

动量守恒题型

题目分类

根据动能是否转化为其它能量可以将动能守恒的题目分为三类：

1. 弹性模型：除动能外，无任何能量生成或损失，即 $E_初 = E_末$。此时动量守恒，动能守恒，做法与弹性碰撞完全一致。

2. 共速模型：两物体相对静止或某方向相对静止，即 $E_初 > E_末$。此时动量守恒，动能损失，计算与非完全弹性碰撞一致。此时能量损失的去向主要是发热量（例如碰撞发热）、重力势能和弹性势能（例如弹簧作为两物体的连接体）。

3. 爆炸模型：通过爆炸/重力做功增加动能，即 $E_初 < E_末$。此时动量守恒，动能增加。

   能量来源：重力势能、弹性势能（两弹簧先压缩再马上松开）、化学能（爆炸）。

除此之外，还有一类特殊的动量守恒模型——人船模型：

$P_初 = 0$，同时由于动量守恒，整个系统动量始终为 $0$，根据动量守恒有：

人船模型

基本知识

判定标准：初动量为 $0$。

特征：人动船动，人停船停。

一般动量的题目涉及与位移有关的题目只能是人船模型。

解题步骤：

1. 判断题目中的系统是否动量守恒，或在某一个方向上动量守恒。
2. 判断是否初动量为 $0$。
3. 若是，则列出（该方向上）有关人船模型的两个公式。
4. 解方程求解。

---

模型：如图所示，长为 $L$，质量为 $m_船$ 的小船停在静水中，一个质量为 $m_人$ 的人站在船头，若不计水的阻力，当人从船头走到船尾的过程中人的位移是 $s_1 = \pu{6m}$。

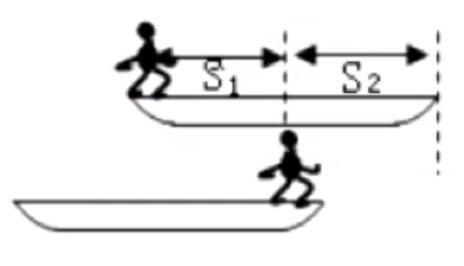
推导：

对于人船系统分析，首先由于水平方向上系统不受力，竖直方向上没有加速度，所以系统动量守恒。

根据动量守恒有

所以人和船每时每刻的动量大小相等，方向相反，所以平均情况下人的动量等于船的动量，即

其中 $\overline{v}$ 表示平均速度，根据运动学公式可知 $\overline v = \dfrac{x}{t}$，即平均速度等于位移除以时间。

由题意得人的位移（相对地面）大小是 $x_人 = s_1$，同理船的位移（相对地面）大小为 $x_船 = s_2$，二者相对位移大小为 $x_{相对} = s_1 + s_2$，那么有

小结论：

例题

例 1：如图所示，一个质量为 $m_1 = \pu{50 kg}$ 的人抓在一只大气球下方，气球下面有一根长绳，气球和长绳的总质量为 $m_2 = \pu{20 kg}$，长绳下端刚好和水平面接触，当静止时人离地面的高度为 $h = \pu{10m}$，如果这个人开始沿绳向下滑，当他滑到绳下端时，他距离地面的高度是多少？

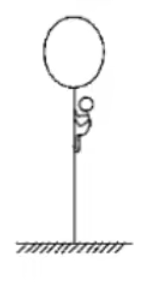
分析：

首先原题目符合动量守恒，且初动量为 $0$（初始状态下静止），所以属于人船模型。

那么根据人船模型的式子可知：

所以距离地面的高度为 $10 - \dfrac {20}{7} = \dfrac {50}{7}\ \pu m$。

注意：

• 人在往下滑时，气球会往上移动。
• 最后求得的 $x_1$ 是相对地面的位移，离地高度还需要用 $10$ 减去 $x_1$。

---

例 2：如图所示，质量为 $m$，半径为 $R$ 的小球，放在半径为 $2R$，质量为 $2m$ 的大空心球内，大球开始静止在光滑的水平面上。当小球从图示位置无初速度地沿大球内壁滚到最低点时，大球移动的距离是多少？

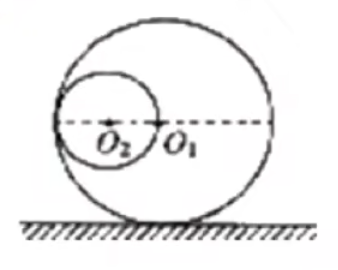
分析：

首先对大小球组成的整个系统受力分析可知，水平方向上不受力，处于平衡状态，所以水平方向上动量守恒；竖直方向上大球静止，小球存在加速度，所以不守恒。那么考虑水平方向上的动量守恒即可。

由于开始系统静止，所以初动量为 $0$，所以是人船模型。

那么列出人船模型的两个公式：

所以大球移动的距离为 $\dfrac R 3$。

注意：这里小球相对大球水平位移是 $R$，而不是 $2R$，看的是小球球心在水平方向上移动的距离。

爆炸模型

基础知识

特征：通过爆炸/重力做功的形式产生能量（能量增多）。

列式：

动量守恒：

增加的能量：

例题

例：如图所示，半径为 $R$，质量为 $M$ 的 $\dfrac 1 4$ 光滑圆槽置于光滑的水平地面上，一个质量为 $m$ 的小木块从槽的顶端由静止滑下，则木块从槽口滑出时的速度大小为多少？

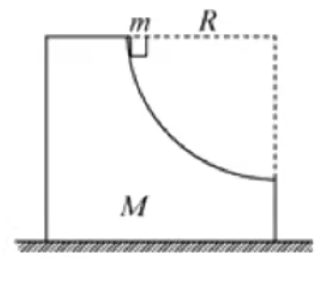
分析：

首先分析可知木块与圆槽组成的系统水平方向上动量守恒，竖直方向上动量不守恒。动能增加，说明是爆炸模型。

对于水平方向，根据动量守恒和动能定理有：

所以木块从槽口滑出时的速度大小为 $\sqrt{\dfrac{2 \mathrm g RM}{m + M}}$。

注意：

• 这道题没有涉及到位移，所以虽然它初动量为 $0$，但不属于人船模型。
• 爆炸模型此类题求速度一般需要列动能定理的式子。
• 一般情况下判断爆炸模型的标准是动能增加，且一般情况下动能来源是重力势能涉及到的计算量较大。

凹槽模型

特征：有形如下图中结构，即 $\dfrac 1 4$ 圆弧的题目一般都属于凹槽模型。

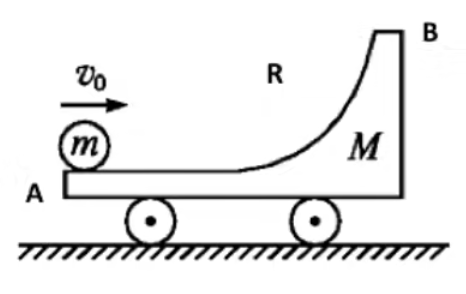
理论依据：只要地面光滑，则水平方向一定动量守恒。

题目分类：

考法一

模型：

以上图为例，一个质量为 $M$，上表面光滑的凹槽在光滑水平面上，质量为 $m$ 的小球从光滑凹槽左端 $A$ 点出发，以初速度 $v_0$ 冲上凹槽，求：

1. （共速模型求速度）当小球运动到 $B$（最高点）时，小球即将做什么运动？此时小球的速度是多少？
2. （共速模型求最大高度）小球运动的最大高度是多少，请对 $R$ 的取值进行分类讨论判断是否滑出最高点（已知 $m = \pu{2 kg}$，初速度 $\pu{6 m/s}$，$M = \pu{4 kg}$）。
3. （弹性模型）当小球运动回 $A$ 时，数据同上，求此时 $m,M$ 的速度分别是多少？$m$ 即将脱离凹槽做何种运动（向右平抛、向左平抛还是自由落体）？

推导：

当小球从凹槽右端运动到最高点时，此时小车有向右的速度，小车相对小车做竖直上抛运动，所以在水平方向上小车与小球没有相对运动，所以二者水平共速。所以小车此时相对地面同时具有水平向右的速度和水平向上的速度，合速度斜向上，所以小球相对地面做斜抛运动。

小球与小车共速说明动能损失，小球损失的动能转化为重力势能。

对于第一问：

根据动量定理有：

对于第二问：

代入第二问给定的值可知

所以根据动能定理有

则当 $R < \pu{1.2 m}$ 时，能够滑出最高点；反之，不能滑出最高点。

对于第三问：

由于 $m$ 与 $M$ 水平方向上共速，所以当 $m$ 到达最高点后，会相对 $M$ 做自由落体运动，然后落入凹槽，从 $B$ 点回到 $A$ 点。

考虑对从 $A$ 点出发到回到 $A$ 点的整个运动过程进行分析，整个过程中，水平方向上动量守恒，且动能没有转化为任何其他形式的能，即动能也守恒，所以属于「弹性模型」。

设末状态 $m$ 的速度为 $v_1$，$M$ 的速度为 $v_2$，那么有

那么由于 $v_1 = \pu{-2 m/s}$，所以 $m$ 做初速度水平向左的平抛运动，即向左平抛。

总结：

• 若题目求的是有关 $B$ 点的信息，则是共速模型，此时小车与小球在水平方向上共速，一般问法为求速度、求高度和求做功（做功用动能定理求解）。
• 若题目求的是回到 $A$ 点后的信息，则是弹性模型，此时动能守恒，一般问法是求速度和求做功（做功用动能定理求解）。

注意：对于第三问，若凹槽上表面粗糙，则会有摩擦生热，即动能不守恒，损失的动能转化为热量，可以求出速度再求出动能损失量计算。

考法二

模型：

如下图所示，一个质量为 $M$，上表面光滑的凹槽在光滑水平面上，质量为 $m$ 的小球从 $B$ 点由静止释放，运动到 $A$ 点，求：

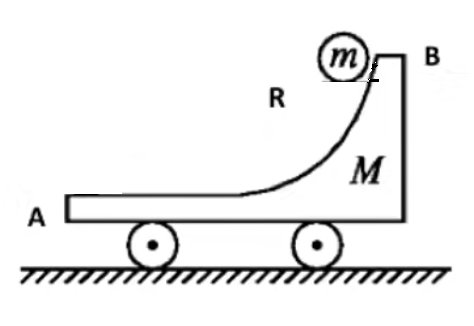
1. （爆炸模型）小球/小车的速度是多少？
2. （人船模型）小球/小车的位移是多少？

分析：

对于第一问：

水平方向上动量守恒，且重力势能转化为动能使得动能增加，所以本质上是爆炸模型。

设 $m$ 和 $M$ 的速度分别为 $v_1$ 和 $v_2$，那么有

解出方程即可求解，做法几乎与爆炸模型完全一致，这里不做赘述。

对于第二问：

求位移，且初动量为 $0$，说明是人船模型。

设 $m$ 和 $M$ 的位移分别为 $x_1$ 和 $x_2$，那么有：

其中 $L$ 表示水平轨道的长度。

总结：

• 从 $B$ 点由静止出发，求速度：爆炸模型。
• 从 $B$ 点由静止出发，求位移：人船模型。

弹簧模型

求弹簧压缩最大时的物理量

问题模型：如下图所示，在光滑水平面上，质量为 $m_1$ 的小球以初速度 $v_1$ 向左运动，其右侧有一个质量为 $m_2$，且左边粘着弹簧的小球，当 $m_1$ 开始运动到弹簧压缩最大时，求二者此时的速度，并求出这个过程中损失的动能。

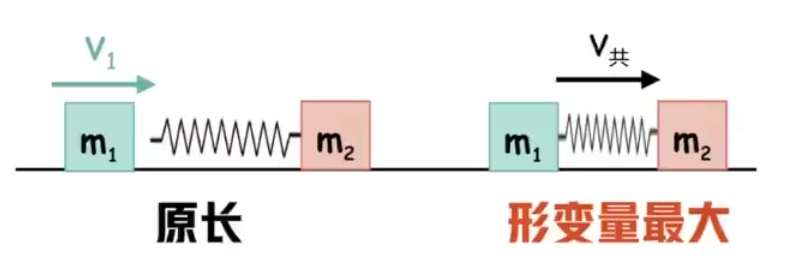
分析：

首先，系统的整个运动过程为：$m_1$ 向左运动直至与弹簧接触，然后随着弹簧的压缩，$m_2$ 开始运动，此时弹簧对 $m_1$ 的力水平向左，弹簧对 $m_2$ 的力水平向右，所以 $m_1$ 减速向左运动，$m_2$ 加速向右运动，当弹簧压缩量最大时，二者共速。

弹簧压缩量最大时二者共速的原因：设二者速度分别为 $v_1$ 和 $v_2$，若 $v_1 > v_2$，则弹簧继续压缩，压缩量不会达到最大；若 $v_1 < v_2$，则弹簧会伸长，也不会保持压缩量最大。所以弹簧压缩量最大时二者共速。

设而这共速时速度为 $v$，受力分析可知，整个系统在整个过程中动量守恒，那么有

同时根据能量守恒定律有

这里损失的动能 $E_损$ 即为弹性势能 $E_{P~弹}$ 的最大值。

整个求解过程中相当于完全非弹性碰撞。

求分离速度

问题模型：在上个问题模型的前提下，$m_1$ 和 $m_2$ 从弹簧压缩最大到逐渐分离，当弹簧变为原长，二者即将分离时，求二者的速度。

分析：

从整个运动过程开始到结束，$m_1,m_2$ 和弹簧组成的系统动能和动量均守恒，那么本质上是弹性碰撞。

那么根据弹性碰撞的求解方法有：

在整个过程中，弹簧对 $m_1$ 的力水平向左，对 $m_2$ 的力水平向右，那么在弹簧恢复原长之前，一直处于压缩状态，那么对 $m_2$ 一直有一个向右的加速度，所以恢复原长之前，$m_2$ 速度一直在增加。恢复原长之后，弹簧对 $m_2$ 的力消失，$m_2$ 向右做匀速直线运动。所以求得的 ${v_2}'$ 是 $m_2$ 的最大速度。

同时在弹簧恢复原长后，$m_1$ 会与弹簧分开，所以最后求得的 ${v_1}'$ 是 $m_1$ 的分离速度。

总结

弹簧模型实际上相当于是放慢的碰撞模型，其本质模型也一般与碰撞模型息息相关。

对于弹簧模型，研究的阶段不同，对应的本质模型也不同：

• 研究从最开始到形变量最大（下图 ①）时，由于最后二者达到共速，所以本质是完全非弹性碰撞。
• 研究从最开始到最终恢复原长（下图 ②）时，由于整个过程动能守恒，所以本质是弹性碰撞。

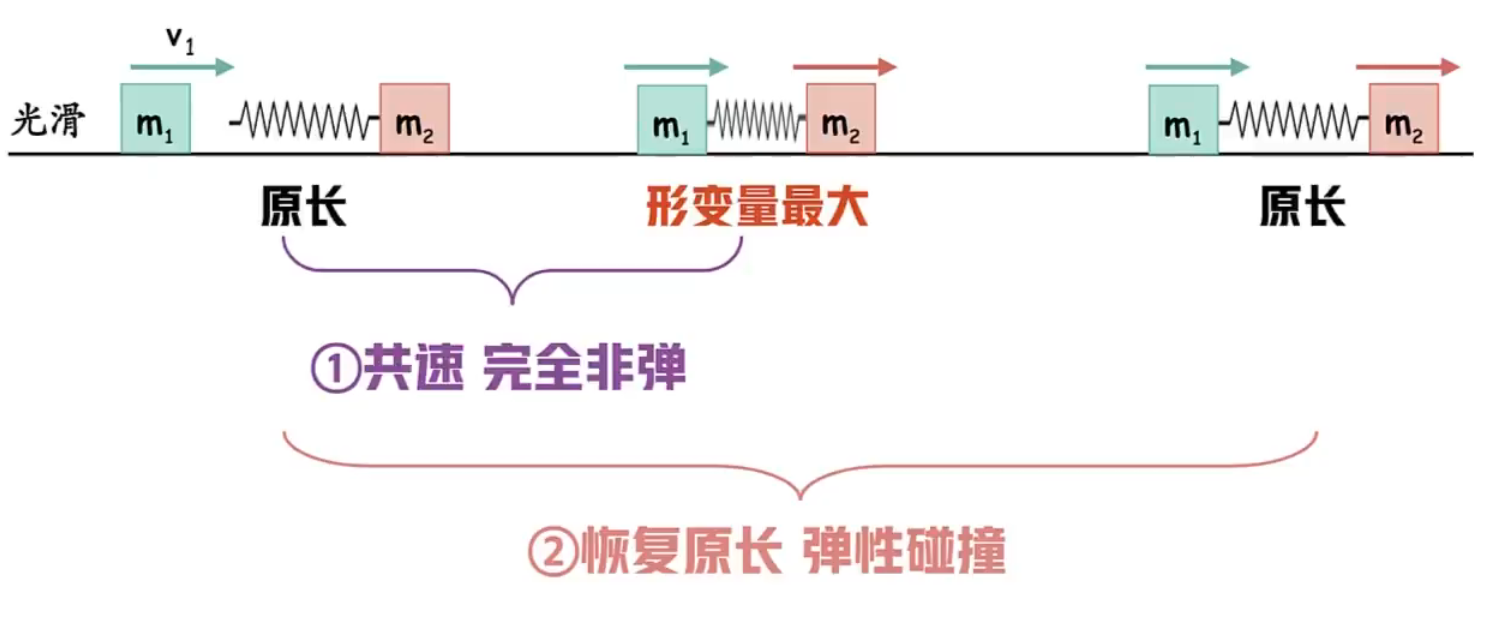
例题

例 1：如图所示，质量分别为 $m$ 和 $2m$ 的 $A,B$ 两个木块间用轻弹簧相连，放在光滑水平面上，$A$ 紧靠竖直墙。用水平力向左推 $B$ 将弹簧压缩，推到一定位置静止时推力大小为 $F_0$，弹簧的弹性势能为 $E$。在此位置突然撤去外力，下列说法中正确的是（）

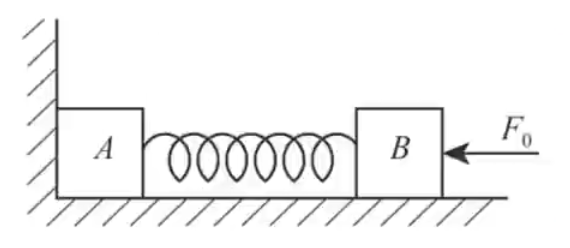
A. 在 $A$ 离开竖直墙前，$A,B$ 与弹簧组成的系统机械能守恒，之后不守恒。

B. 在 $A$ 离开竖直墙前，$A,B$ 系统动量守恒，之后不守恒

C. 在 $A$ 离开竖直墙后，$A,B$ 速度相等时的速度是 $\dfrac 2 3 \sqrt{\dfrac{2E}{m}}$

D. 在 $A$ 离开竖直墙后，弹簧的弹性势能最大值为 $\dfrac E 3$

---

分析：

首先考虑整个运动过程：

• 起初水平推力向左推 $B$，直至静止，此时 $B$ 受到外力 $F_0$，弹簧对 $B$ 向右的弹力，大小与 $F_0$ 相等。$A$ 受到墙壁对它向右的支持力和弹簧对它向左的弹力，二者大小相等且都与 $F_0$ 的大小相等。
• 接着撤去外力，那么此时 $B$ 的合外力与弹簧对它向右的弹力相等，所以 $B$ 有向右的加速度。$A$ 依然保持平衡，保持静止。所以 $B$ 不断向右加速，$A$ 保持静止，弹簧不断伸长。
• 当弹簧伸长到原长时，弹簧对 $A$ 和 $B$ 的力均消失，此时 $B$ 会保持当前速度 $v_0$ 继续做匀速直线运动，而 $A$ 仍然静止。当 $B$ 继续运动时，弹簧伸长，此时对 $A$ 有向右的弹力，$A$ 开始运动。
• 随着弹簧的伸长，其对 $A$ 有向右的弹力，对 $B$ 有向左的弹力，$A$ 不断加速，$B$ 不断减速，直至弹簧伸长量最大时，二者达到共速。

对于 A 选项：

由于 $A$ 离开竖直墙壁前，整个系统只受到墙壁和地面对它的支持力，但支持力方向上没有通过距离，所以做功为 $0$，所以机械能守恒。$A$ 离开竖直墙壁后，整个系统只受到地面对它的支持力，且不通过距离，所以做功为 $0$，所以机械能依然守恒。综上可知，机械能在整个过程保持守恒，A 错误。

对于 B 选项：

在 $A$ 离开竖直墙壁前，系统受到墙壁对它的支持力，所以动量不守恒。$A$ 离开竖直墙壁后，整个系统所受合外力为 $0$，所以动量守恒。综上可知，动量先不守恒然后再守恒，B 错误。

对于 CD 选项：

从 $A$ 离开竖直墙壁到二者共速，系统动量守恒，初动量为 $B$ 的动量。设二者共速时速度为 $v$，根据动能定理和动量定理有：

那么接下来就是要求 $v_0$，由于从 $B$ 静止到 $A$ 离开竖直墙前，根据动能定理有

代入前面求得的 $v$ 和 $E_{P~弹}$ 中得：

综合上述，此题应选 D。

---

例 2（碰撞与弹簧结合）：如图所示，地面光滑，质量为 $m_1$ 的 $A$ 物块，以 $v_0 = \pu{10 m/s}$ 的速度向右匀速运动，质量分别为 $m_2,m_3$ 的物块 $B$ 与 $C$，由轻质并且处于原长状态的弹簧相连，$B,C$ 和弹簧初始静止放置，某时刻 $A$ 与 $B$ 碰撞后立刻粘在一起，已知 $m_1 = \pu{2 kg}$，$m_2 = m_3 = \pu{3 kg}$，求：

1. $A$ 与 $B$ 碰撞粘在一起后瞬间的速度大小。
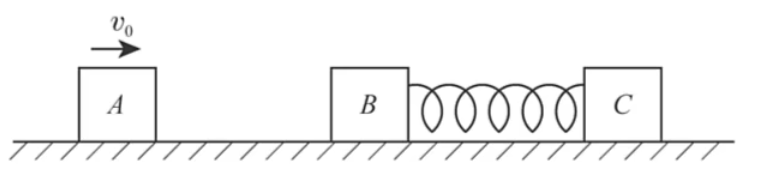
2. 此后运动过程中，弹簧被第一次压缩到最短时的弹性势能大小。

分析：

对于第一问：

定义水平向右为正方向。则从 $A$ 开始到与 $B$ 碰撞，整个过程中动量守恒。

注意：碰撞是「瞬间」发生的。所以两物体碰撞时，不需要考虑其它物体对这两个物体的作用力，即碰撞时两物体一定动量守恒。

设二者粘在一起后共速的速度为 $v$，那么对于 $A,B$ 组成的系统列动量定理有

对于第二问：

$A,B$ 粘在一起后，两个物体一块以 $v$ 的速度向右运动，压缩弹簧，从而使得弹簧给 $C$ 有一个向右的支持力，使得 $C$ 开始向右运动。

设 $A,B,C$ 在弹簧压缩到最短时的速度为 $v'$，从 $A,B$ 开始以 $v$ 的速度向右运动，到弹簧压缩到最短时，对于 $A,B,C$ 和弹簧组成的整个系统有

注意：第二问求弹性势能时，不能直接选取从 $A$ 最开始以 $v_0$ 运动到整个运动结束，因为 $A,B$ 黏在一起时有动能损失。

反冲问题

基本知识

概念：原本在一起的两个物体，靠内力产生反向速度，彼此分离。

常见场景：火箭分离，战斗机加速喷气，在冰面上放屁，人跳车。

关键：运动的改变只靠内力，不靠外力。

思路：考虑到在反冲方向上合外力为 $0$，动量守恒。通过对反冲方向列动量守恒等式求解。

反冲前静止

模型：如下图所示，在光滑平面上，物块 $1$ 和 $2$ 起初连在一起，且都静止，两物体发生反冲。反冲后，物块 $1$ 向左以 $v_1$ 的速度运动，物块 $2$ 向右以 $v_2$ 的速度运动。设物块 $1$ 对 $2$ 的力为 $F_1$，$2$ 对 $1$ 的力为 $F_2$，两个力的冲量分别是 $I_1$ 和 $I_2$，两物体的动量分别为 $P_1$ 和 $P_2$，加速度分别为 $a_1$ 和 $a_2$，速度大小分别为 $v_1$ 和 $v_2$，动能分别为 $E_{k1}$ 和 $E_{k2}$，请比较每一对物理量的大小关系。

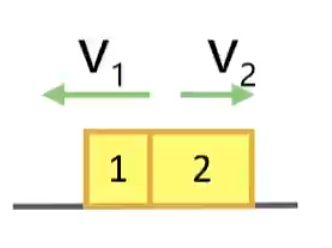
求解：

由于 $F_1$ 和 $F_2$ 是相互作用力，所以两个力大小相等，根据 $I = Ft$ 可知 $I_1$ 和 $I_2$ 大小相等。

以向右为正方向，那么对于物块 $1$ 和 $2$ 组成的系统有：

所以 $I_1$ 和 $I_2$ 大小相等。

又根据 $F = ma$ 可知 $\dfrac{a_1}{a_2} = \dfrac{m_2}{m_1}$；根据 $P = mv$ 可知 $\dfrac{v_1}{v_2} = {m_2}{m_1}$。

对于动能有：

结论：两物体反冲模型中，所受力的大小、冲量大小和动量大小无论质量如何始终相等，加速度大小、速度大小和动能大小之比等于两物体质量的反比。

注：题目中若求力做功之比，可以根据动能定理转化为求动能之比。

例题

例 1：将静置在地面上，质量为 $M$（含燃料）的火箭模型点火升空，在极短时间内以相对地面的速度 $v_0$ 竖直向下喷出质量为 $m$ 的炽热气体。忽略喷气过程中重力和空气阻力的影响，则喷气结束时火箭模型获得的速度大小是多少？

求解：

以向上为正方向，设火箭模型获得的速度为 $v$，考虑对火箭和气体组成的系统分析，根据动量定理有：

注意：火箭喷气后质量要记得减去喷出的气体质量。

---

例 2：电影《火星救援》中，宇航员在太空中与飞船之间相距 $\pu{7.5 m}$，飞船无法实施救援活动，为了靠近飞船，男主角剪破自己的宇航服，反向喷出气体使自己飞向飞船。假设气体能以 $\pu{50 m/s}$ 的速度喷出，宇航员连同装备共 $\pu{100 kg}$，开始时宇航员和飞船保持相对静止，宇航员必须在 $\pu{100 s}$ 内到达飞船，喷出气体的质量至少为（）

A. $\pu{0.1 kg}$

B. $\pu{0.15 kg}$

C. $\pu{0.2 kg}$

D. $\pu{0.25 kg}$

---

求解：

以宇航员飞向飞船的方向为正方向，那么将宇航员和喷出气体作为一个系统分析，根据动量守恒有：

此时观察选项可发现，四个选项所给的喷出气体的质量均远小于人的质量，所以在 $100 - m$ 中，$m$ 可以忽略不计。

那么有：

故选 B。

反冲前有初速度

关键：反冲前系统共速，那么有 $(m_1 + m_2) v = m_1 v_1 + m_2 v_2$。

其它大体与反冲前静止的做法相同。

例题

例 1：如图所示，甲、乙两船的总质量（包括船、人和货物）分别为 $10 m、12m$，两船沿同一直线同一方向运动，速率分别为 $2v_0、v_0$，为避免两船相撞，乙船上的人将一质量为 $m$ 的货物沿水平方向抛向甲船，甲船上的人将货物接住。不计水的阻力。则抛出货物的最小速率是多少？

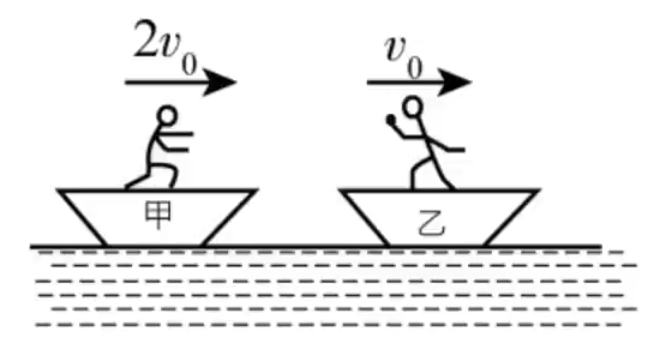
求解：

首先整个题实际上涉及两个反冲过程：先是乙扔出货物时，乙和货物反冲；再是甲接住货物时，甲和货物逆反冲。

乙扔出货物，会导致乙和船向右加速，货物有向左的速度；甲接住货物时，会导致甲和船向左减速，货物变为静止。题目求抛出货物的最小速率，实际上指的是使得甲乙不相撞的临界状态，要使得甲乙不相撞，必须使得乙最终速度 $\ge$ 甲的速度，那么临界状态就是乙的速度 $=$ 甲的速度。

设甲乙最终共速时的速度为 $v_共$，货物的最小速率为 $v$，那么对于两次反冲都有动量定理：

---

例 2：如图所示，甲、乙两船的总质量（包括船、人和货物）分别为 $80 m_0、20 m_0$ 两船沿同一直线相向运动，速度大小为 $2 v_0、v_0$。为避免两船相撞，甲船上的人不断地将质量为 $m_0$ 的货物袋以相对地面 $6.2 v_0$ 的水平速度抛向乙船，且被乙船上的人接住，假设某一次甲船上的人将货物袋抛出且被乙船上的人接住后，刚好可保证两船不致相撞，不计水的阻力。试求此时（）

A. 甲、乙两船的速度大小 $1.4 v_0$

B. 甲、乙两船的速度大小 $1.25 v_0$

C. 从甲船抛出的总货物袋数 $12$ 个

D. 从甲船抛出的总货物袋数 $10$ 个

---

求解：

【法一——整体法】

考虑将甲乙两船及货物袋整个系统分析，可知整个系统动量守恒。定义向右为正方向，设甲乙两船共速时速度为 $v_共$，那么对于整个系统有：

注意：这里不知道 $v_共$ 的方向，可先默认为正方向，然后根据计算得到结果的正负判断方向。

设抛出货物袋的总质量为 $M$，再对甲抛出货物袋时，甲和货物袋整体分析，根据动量定理有：

故选 AD。

【法二——隔离法】

考虑利用例 1 中同样的思路。

同理以向右为正方向，对于两次反冲都有动量定理：

碰撞中的可能值

碰撞需要满足的条件

1. 碰撞一定满足动量守恒。
2. 碰撞前，$v_后 > v_前$，碰撞后 $v_后 < v_前$（若后面速度小于前面速度，后面的小球就会继续撞击前面的小球）
3. 对于动能，有 $E_{k~前} \ge E_{k~后}$，即动能可能损失或不损失，但不可能增加。

三大物理量可能的取值

【速度的范围】

由于从弹性碰撞到完全非弹性碰撞，动能从不损失到损失最大，所以碰撞速度的取值范围是从共速的速度（完全非弹性碰撞）到弹性碰撞的速度之间。可以取等号。

适用于未知末状态任何物理量。

注意：共速时速度不一定最小，弹性碰撞时速度也不一定最大，例如若速度区间为 $[-2,4]$，则速度大小最大为 $4$，但最小是 $0$，而不是 $-2$。

【损失动能的取值范围】

从 $0$（弹性碰撞）到完全非弹性碰撞损失的能量。

动能和速度不同，完全非弹性碰撞损失能量一定是最大的，弹性碰撞损失的能量一定是最小的。

【动量的变化可能取值】

一定存在的约束：两物体动量变化相加为 $0$ 或动量守恒（即 $A$ 物体动能变化为 $+2$ 则 $B$ 物体变化一定为 $-2$）。

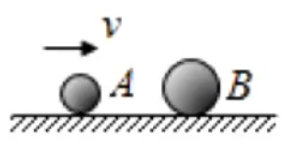
对题目分类有两种情况：

• 若 $m$ 未知：以上图为例，设 $A$ 初始时动量为 $P_A$，撞击后动量为 ${P_A}'$。首先考虑动量变化最大的情况，那么当 $B$ 物体的质量 $m_B$ 趋近于 $+\infty$ 时，$v_B$ 趋近于 $0$，相当于 $A$ 撞上一堵墙后反弹，此时 $A$ 动量改变后，会趋近于 $-P_A$，变化量 $\Delta P$ 趋近于 $-2P_A$（取不到）；再考虑变化最小的情况，当 $A,B$ 两物体速度差无限趋近于 $0$ 时，$A$ 撞到 $B$ 速度变化量也无限趋近于 $0$，$A$ 的动量变化量 $\Delta P$ 无限趋近于 $0$（取不到）。所以碰撞后 $A$ 的动量 ${P_A}' \in (-P_A,P_A)$，动量变化量 $\Delta P \in (-2P_A,0)$。
• 若 $m$ 已知：根据 $P = mv$，则速度可以求出，本质上相当于求速度取值范围。

注意：若题目求的是 $B$ 的动量变化范围，则应该先求出 $A$ 的动量变化范围，再推出，不能想当然的以为是 $(-2P_B,0)$，不符合动量守恒。

解题时的注意事项&易错点

1. 利用动量相关公式时，计算时速度需要带符号计算，不能只代入大小。
2. 求解碰撞相关题目时，不能引入涉及到碰撞外的其它物体。且碰撞是一个瞬间，碰撞一瞬间其他物体的速度不会发生任何变化。
3. 利用动量求解平均作用力时，需要注意这里的平均作用力是否等于合外力，比如 $F_合 = F_N - m \mathrm g$ 时，此时支持力的平均作用力应该是合力的平均作用力加上重力。
4. 若两物体碰撞后黏在一起，后续计算需要将两物体看成一个整体，质量为 $m_1 + m_2$，而不是 $m_1$。