【文化课学习笔记】【物理】实验:验证机械能守恒定律
【物理】实验:验证机械能守恒定律
自由落体验证机械能守恒定律
实验目的
验证机械能守恒定律。
实验原理
求出做自由落体的物体的重力势能的减少量和动能的增加量。
在实验误差允许范围内,若二者相等,则说明机械能守恒,从而验证了机械能守恒定律。
实验器材
重物、打点计时器、交流电源、纸带、刻度尺、铁架台(带铁夹)。
注意:不需要秒表和天平。所有需要使用打点计时器的实验均不需要秒表。且由于此实验中,是根据
计算的,此时两遍都可以约去 ,所以 测得的结果精确与否对实验无影响。
实验过程
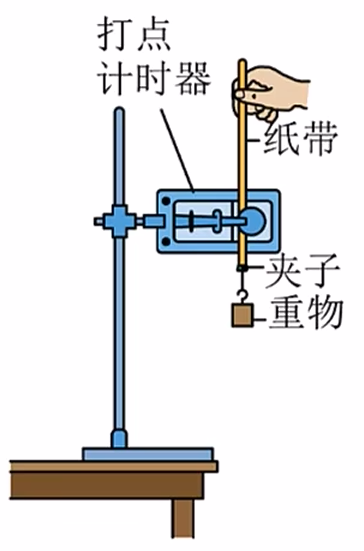
【安装器材】
讲打点计时器固定在铁架台上,用导线将打点计时器与电源相连。
【打纸带】
用手竖直提起纸带,使重物停靠在打点计时器下方附近。先接通电源,再松开纸带,让重物自由下落,打点计时器就在纸带上打出一系列点,取下纸带,换上新纸带重打
注意:
- 需要用手竖直提起纸带,而不能用手在下方托住重物,是为了避免纸带在下落的过程中跟打点计时器之间有摩擦生热。
- 重物要停靠在打点计时器下方附近,目的是为了多打点。
- 打
条纸带的目的是保证打点的纸带上点较为清晰。
【数据处理】
选择点迹清晰的纸带,验证机械能守恒定律。
数据处理
方案一
利用起点和第
- 选择第
- 测出从起点到第
- 计算第
若在误差范围内,
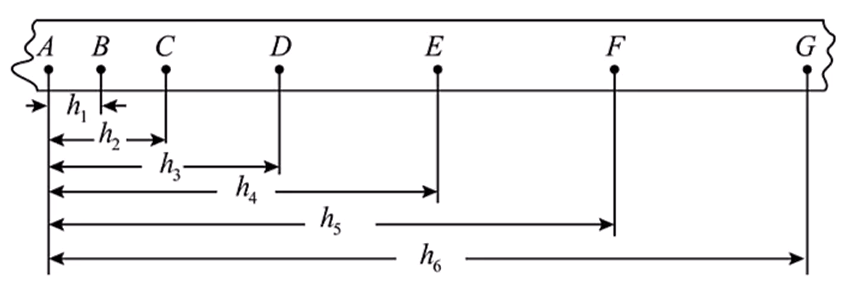
方案二
任取两点
- 测出
- 测出
若在误差范围内,
方案三
原理:
根据机械能守恒定律的式子
图象法:
- 测量从起点到剩余各点的下落高度
- 以
若在误差范围内,图象是一条过原点且斜率为
注意事项
- 安装打点计时器时,要使其两限位孔在同一竖直平面以减少摩擦。
- 重物的密度要大。目的:体积相同时,密度越大,重力越大,更能满足重力远大于空气阻力。
- 释放前提着纸带,而不是拖着重物。目的:减少纸带与打点计时器之间的摩擦。
- 重物靠近打点计时器。目的:多打点。
- 先接通电源,再松开纸带让重物下落。
- 计算速度不可用
- 实验仪器不需要秒表和天平。
误差分析
若
若
- 利用方案
- 交流电的频率变小了。根据
其它方法验证机械能守恒定律
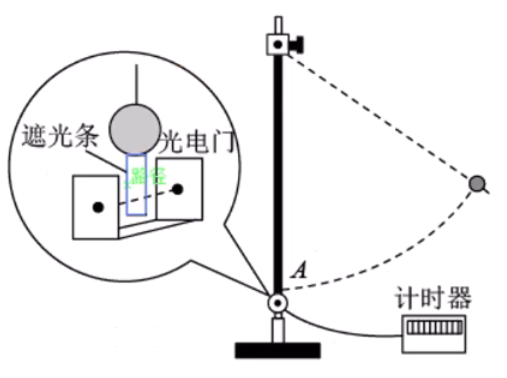
光电门测速
遮光条通过光电门的时间很短,设遮光条的宽度为
注意:遮光条的宽度不能太长,遮光条通过光电门的速度不能太慢。若
太长, 太慢,会导致时间 变长,会使得近似不再准确。
竖直双物块模型
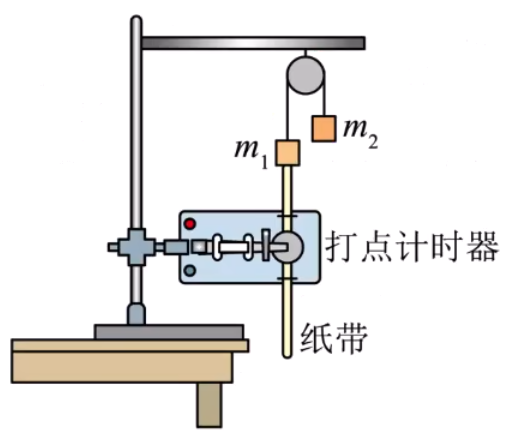
如图所示,
那么整个系统机械能守恒,则一定有
那么要使用该系统验证机械能守恒定律,需要利用天平测出两物块质量
注意:在双物块模型中,物块质量不能约去,所以不能不测量。
斜面双物块模型
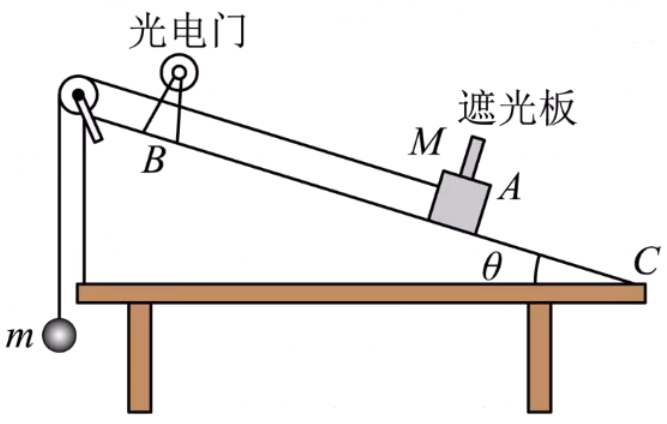
如图所示,物块的质量是
假设物块从
分别计算出左右两边的式子,若二者在误差范围内相等,则验证了机械能守恒定律。
注意:在这种模型下,同样需要将
和 准确测出。
竖直圆模型
如图所示,设小球从释放到下落的高度为
误差分析:此时由于
例题
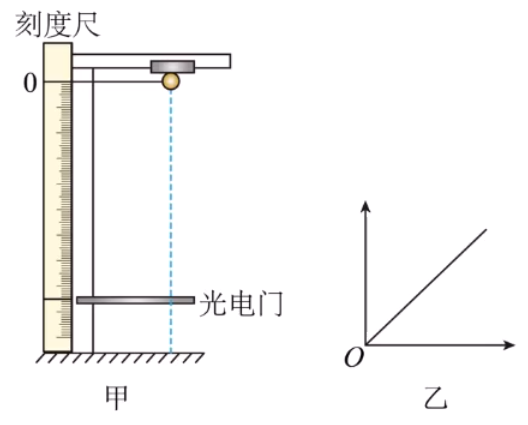
晓强利用如图甲所示的装置完成了机械能守恒定律的验证,将体积较小的球由一定高度处静止释放,经过一段时间,小球通过固定在下侧的光电门,光电门记录了小球挡光时间
-
实验时,下列正确的是()
A. 应选择直径较大的铝球
B. 应选择直径较小的钢球
C. 小球的释放点距离光电门越近越好
D. 小球的释放点到光电门的距离适当远些
-
如果小球的直径为
-
如果利用得到的实验数据描绘图象,纵轴为
分析:
对于 1,要使得求得的近似值更加准确,应该要让直径
对于 2,根据光电门测速可知,若小球的直径为
对于 3,对于第 2 问的式子变形可知
注意:对于第二问第二小问,已知机械能守恒求关系式,若已知小球质量,则对应关系式需要包含
;若未知小球质量,则需要约去 。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· 什么是nginx的强缓存和协商缓存
· 一文读懂知识蒸馏
· Manus爆火,是硬核还是营销?