【物理】曲线运动
曲线运动
基础概念
物体做曲线运动的条件:有 a v a , v a F 合
运动轨迹的特点:a ( F 合 )
曲线运动的加速/减速:a , v a , v
方向:曲线运动一般研究两个方向,某个点的切线 方向和垂线 方向。
合运动与分运动
水平方向匀速直线 + a
水平方向匀速直线 + a v a , v
水平方向匀变速直线 + a , v v x v y = a x a y a , v
注意:
肉眼看不到分运动,只能看到合运动。
水平和竖直方向上的分运动的时间 一定相等,且两个分运动互不影响。
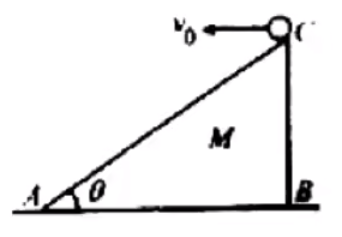
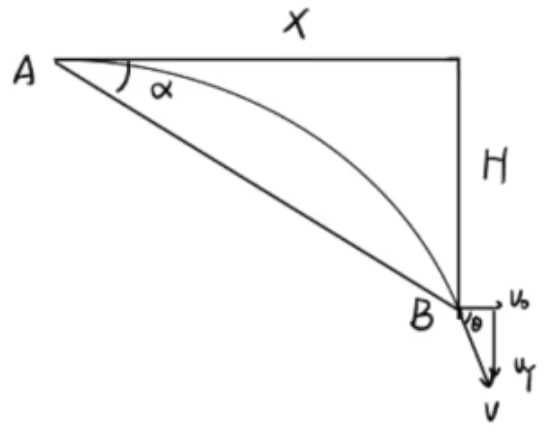
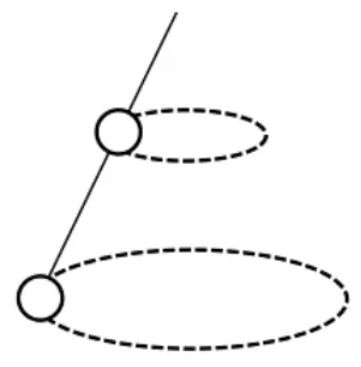
小船过河
问法:①求最短渡河时间;②求最短渡河位移。
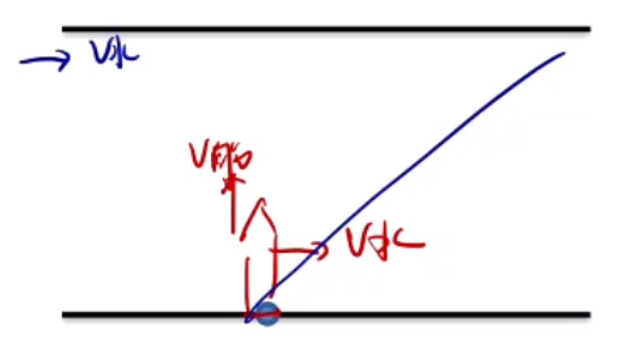
水平速度的作用:让船横着动。
竖直速度的作用:让船渡河。
物理量:v 船 , v 水 , v v x , v y d x 平 x t d
那么有
v 船 > v 水 最短渡河时间:
由于 d t d v y v 船 v 船 θ v y = v 船 cos θ v y v y = v 船 v 船 t d = v 船 d
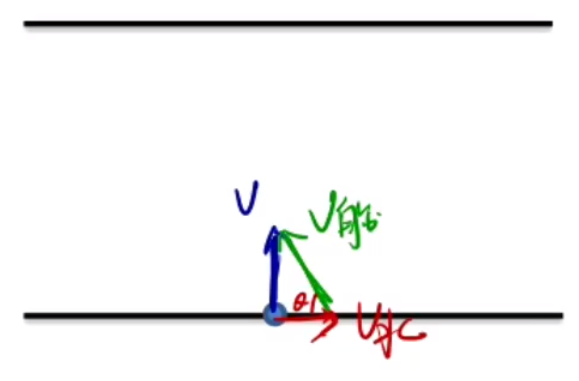
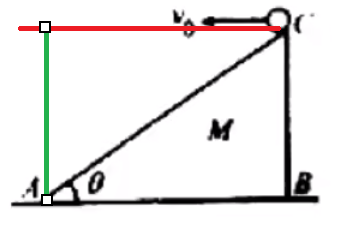
最短渡河位移:
要使得 x x v v y = v v 船 θ v y = v = v 船 sin θ
此时,v 船 必须满足 v 船 > v 水 。
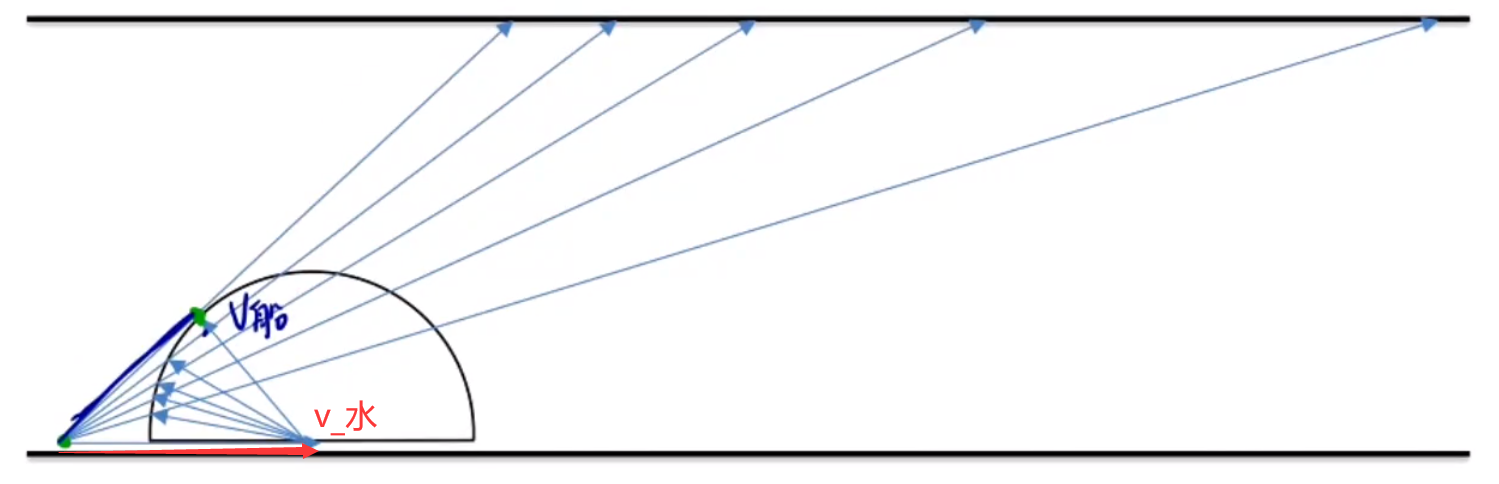
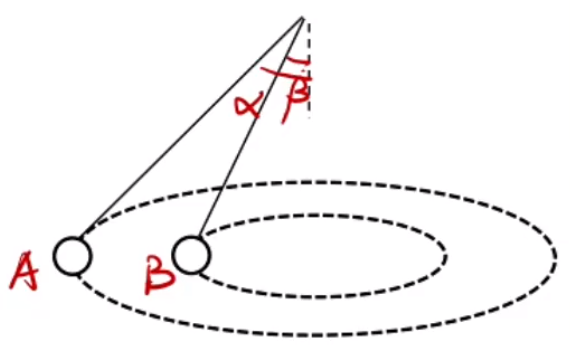
v 水 > v 船 最短渡河时间:由于水平方向与竖直方向的运动互不影响 ,渡河是竖直方向的运动,所以此时的情况同 v 船 > v 水
最短位移渡河:
如图所示,v 水 v 船 v 船 ⊥ v x v θ x = v t d = v ⋅ v y d = v ⋅ v sin θ d = sin θ d
关联速度
现象:①沿绳、沿杆方向速度大小相等;②垂直于接触面方向速度大小相等。
求解方法:
判断合运动方向。
分解合运动到沿绳、沿杆或垂直于接触面方向,即沿绳、沿杆或垂直于接触面建系。
根据现象速度相等列等式求解问题。
注意:沿杆模型 和有杆的接触面模型 有时候易混,区别是沿杆模型中杆的两端都是可以动的 ,而有杆的接触面 中,杆有一端被固定,不能移动 。
平抛运动
本质(定义)
一个物体水平方向上有 v 0
水平方向以 v 0 v 平 = v 0 t
竖直方向是自由落体运动,运动时间 t 只与高度有关 。
基础平抛计算
思路:将合运动分为水平和竖直方向上的两个分运动去解。
水平方向:x = v 0 t
竖直方向:h = 2 1 g t 2 , v t = g t
对于图中经过多个点的平抛运动,考虑将从起点开始 到中间每个点的水平方向和竖直方向上的等式都列出然后再代值求解。
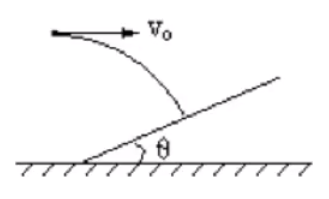
带角度平抛计算
求解思路
题目给的有角度的两类物理量:①位移;②速度。
思路:
首先判断题目给定的角度是位移 的角度还是速度 的角度:如果能明确画出末速度方向,则给定的是速度角度。一般情况下会以两种方式告知:会告诉物体如何落地(比如垂直落在斜面上)或恰好 落在某地(比如恰好相切)之类的词语。否则给定的是位移角度。
列出对应的水平方向和竖直方向的等式:
给定位移角度:通过水平方向上的 x = v 0 t h = 2 1 g t 2
给定速度角度:则通过水平方向上 v x = v 0 v y = g t
通过角度把 x y
位移角度:画出水平位移和竖直位移,找出位移角度。
速度角度:画出水平速度和竖直速度,找速度角度。
例题
例 1:如图,从倾角为 θ v 0
分析:
发现题目中没有给定明确的速度角度信息,所以考虑分析位移角度。
那么有:
画图图象可知:
竖直位移比水平位移为 tan θ
tan θ = x h = v 0 t 2 1 g t 2 ⟹ t = g 2 v 0 tan θ
例 2:如图,水平速度抛出的物体,飞行 3 θ = 3 0 ∘ g 10 m / s 2 v 0
分析:
由于题面给定物体垂直落在斜面上,说明给定了速度角度。
那么有:
{ v x = v 0 v y = g t
画图可知:
水平速度比竖直速度为 tan θ
tan θ = g t v 0 ⟹ v 0 = 10 m / s
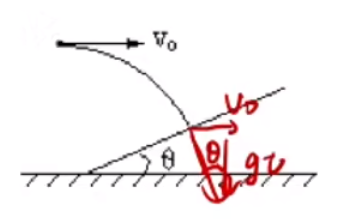
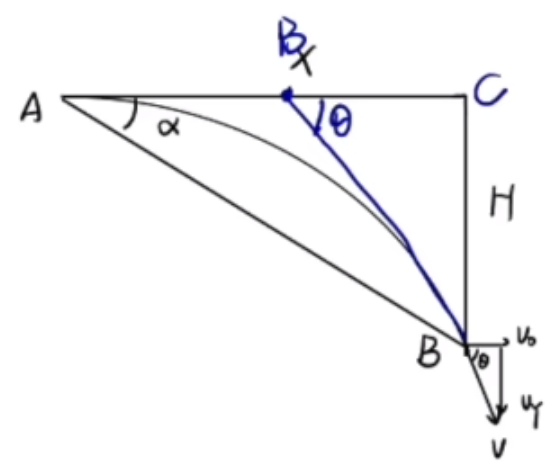
位移角度与速度角度的关系
推导:
如图所示,那么有:
tan α = x h = v 0 t 2 1 g t 2 = 2 v 0 g t tan θ = v 0 v y = v 0 g t
所以 tan θ = 2 tan α 将末速度反向延长,过水平位移中点 ,如图所示:
此结论可证明一小球从同一斜面的某个固定的点出发,以不同初速度,到达斜面的速度方向相同。
原因:位移角度不发生变化,所以位移角度不会发生变化。
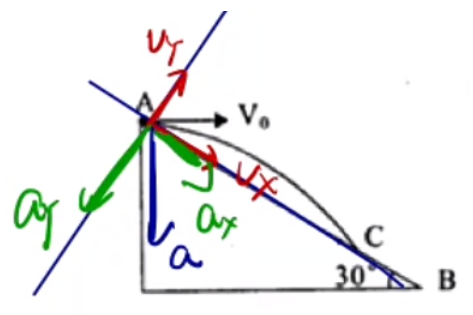
斜面最远距离
问题模型:求小球从斜面顶端以水平初速度 v 0
思路:
首先以斜面方向和与斜面垂直的方向建系,然后将所有的物理量分解到这两个方向上。那么原来水平的初速度会有两个分速度 v x v y a x a y y y 0
计算:
以斜面与水平面夹角是 3 0 ∘ 0 t
t = a Δ v = − a y 0 − v y = g cos 3 0 ∘ v 0 sin 3 0 ∘
小球与斜面间距离最大的高度 h
− 2 a y h = 0 − v y 2 ⟹ h = 2 a y v y 2
总结:建系方向与题目所研究的方向一致时,有时计算会更加简便。
斜抛运动
定义:沿着斜向上以一定初速度抛出一个物体的运动。
本质:初速度倾斜,只受重力。
运动:
水平方向:匀速直线运动。
竖直方向:竖直上抛运动。
从最高点到最低点的过程是平抛运动。
思路:
设初速度为 v 0 v x = v 0 cos θ v y = v 0 sin θ
所以水平方向的位移 x = v 0 sin θ ⋅ t v t = v 0 sin θ − g t y = v 0 sin θ ⋅ t − 2 1 g t 2 y = 0
最高点:
速度方向是水平方向。
速度大小等于此时水平的速度大小 v = v 0 cos θ
对于斜抛运动而言,任何情况下,只要物体运动到最高点/最低点,v y 0
对称性:
运动轨迹关于最高点成轴对称,所以对称点的速度大小相同,方向相反 ,对称的路程所用的时间相同 。
特征:
斜抛运动的轨迹与质量无关 。
斜抛运动的射程与抛射的初速度 和角度 有关。
最远射程:
若角度固定,则 v 0
当 v 0
y = v 0 sin θ ⋅ t − 2 1 g t 2 = 0 ⟹ t = g 2 v 0 sin θ
又因为
x = v 0 cos θ ⋅ t = v 0 cos θ ⋅ g 2 v 0 sin θ = g 2 v 0 2 sin θ ⋅ cos θ = g v 0 2 sin 2 θ
所以当 sin 2 θ x y = sin 2 θ θ ∈ [ 0 , 9 0 ∘ ] sin 2 θ = 1 θ = 4 5 ∘ θ = 4 5 ∘ x = g v 0 2
圆周运动
圆周运动的物理量
【线速度】
定义:弧长/时间。符号:v 线 v m / s v 线 = t A B ⌢
【角速度】
定义:角度/时间。符号:ω rad / s ω = t θ
【周期】
定义:完成一次所用的时间。符号:T s
【频率】
定义:1 s f Hz
【转速】
定义:1 s n r / s
匀速圆周运动
概念
速度大小不变(方向改变)的圆周运动。
匀速圆周运动线速度和角速度大小均不变,同时角速度方向也不变。
基础公式
以匀速圆周运动一圈为研究对象。
⎩ ⎨ ⎧ v 线 = t A B ⌢ = T 2 π R ω = t θ = T 2 π ⟹ v 线 = ω R
次要公式
T = ω 2 π f = T 1 n = f
周期 T f n
传动装置
同轴转动
特征
一个物体上所有的点,角速度 ω
模型一
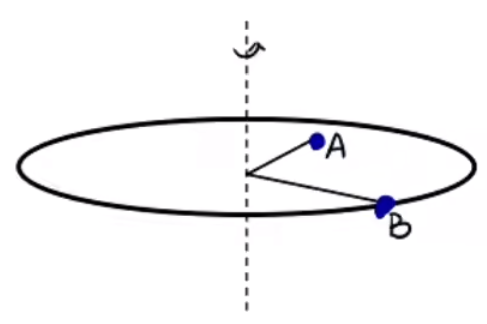
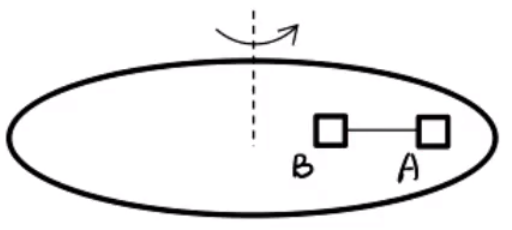
如图,点 A B B ω A = ω B , v B > v A
逻辑上,可以通过 ω A = ω B v = ω R R A < R B v A < v B
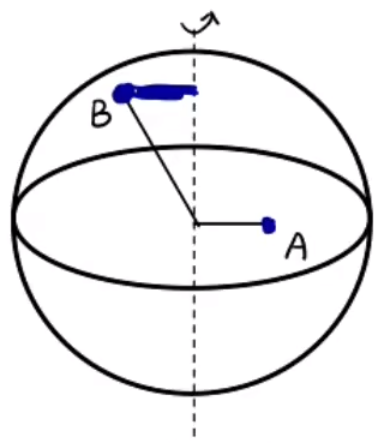
模型二
如图,则分析可知 ω A = ω B v = ω R R A < R B v A < v B
模型三
同理,ω A = ω B A , B
注意:B B
共线转动
特征
多个物体之间,其最外围 的线速度 v
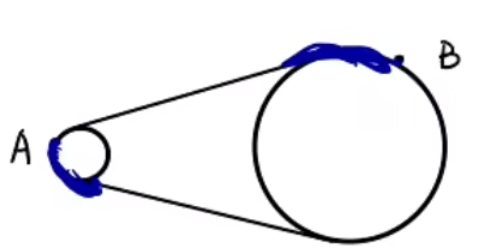
模型一
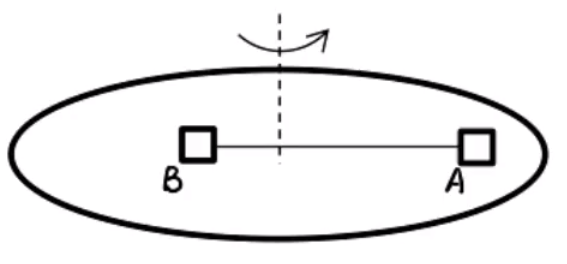
如图,则 v A = v B v = ω R R A < R B ω A > ω B
模型二
同理,v A = v B R A < R B ω A > ω B
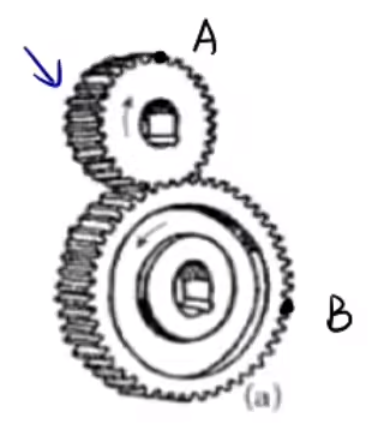
对于齿轮问题,齿轮数之比 = =
圆周运动中的牛二
推导过程
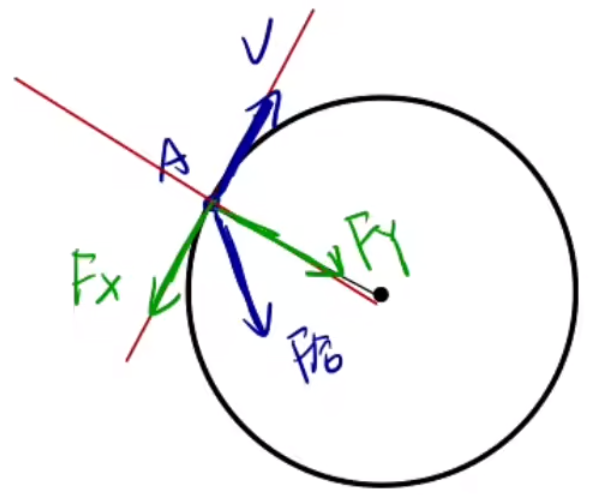
圆周运动 → v → a →
圆周运动研究的两个方向
圆心方向和切线方向。所以一般以这两个方向为 x , y
那么如图所示:
假设速度 v F 合 F 合 x , y F x F y
那么在 x 切线方向 F x 。
在 y F y 只改变速度的方向 。
向心力与向心加速度
依照上图,将物体所受合外力 F 合 F y 本身并不存在 ,所以物体不会受到向心力 。
将物体加速度 a a y
在匀速圆周运动 中,a x = 0 F x = 0 F 合 = F y a = a y
公式
a 向 = r v 2 = r ( ω r ) 2 = ω 2 r = ( T 2 π ) 2 r F 向 = m a 向 = m ⋅ r v 2 = m ω 2 r
上述两个公式适用于任何圆周运动。
物体中各点线速度角速度的大小比较
方法:列表法。
求解步骤:
填列:有几个物体就写几列。
填行:根据对应物体的物理量填行。第一行填半径 r ω v a
找相同角速度:找题中相同 ω ω = 1
找相同线速度:找题中相同 v v = ω R ω
求加速度:根据 a = r v 2
若题目求周期 T T 1 : T 2 : T 3 = ω 1 1 : ω 2 1 : ω 3 1
匀速圆周运动中的模型
解题思路
特征:匀速圆周运动绝大多数出现在水平面 上的运动,非匀速圆周运动大多出现在竖直面上的运动。
关键:通过受力分析将运动学与力学联系起来。
建系:以切线方向和圆心方向分别作为 x , y
列式:利用正交分解列式,其中 x y
{ x : F 左 = F 右 y : F 合 = F 大 − F 小
求解:求出 r F 合 = F 向 = m r v 2 = m ω 2 r
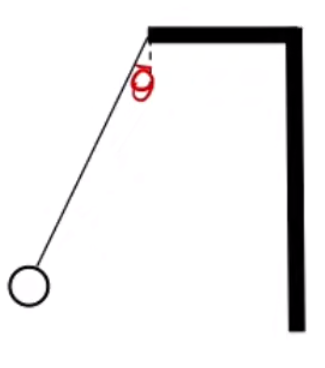
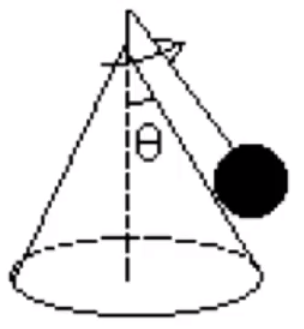
【模型一】圆锥摆基础模型
如图,有一长度为 L θ ω
求解:
以圆心方向为 x
{ F 合 = T sin θ T cos θ = m g
再根据 F 合 = F 向 T sin θ = m ω 2 r r = L sin θ m g tan θ = m ω 2 L sin θ ω = L sin θ g tan θ = L cos θ g
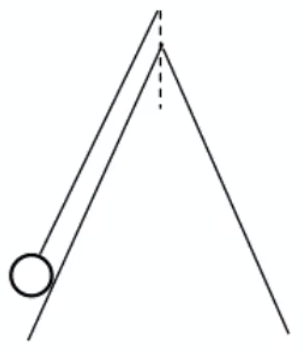
情况一:v 如图,长为 L 0 O C a ω
分析:
首先,当小球碰到钉子时,小球的线速度 v 。原因:一般情况下题目会告知「系统的能量损失忽略不计」,那么此时动能没有损失,所以线速度不变。
同时当小球碰到钉子时,小球圆周运动的半径变小,根据 v a = r v 2 a v = r ω v r ω
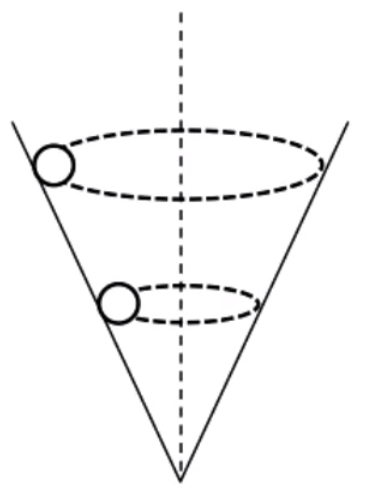
情况二:同角不同面(a
如图所示,在一个漏斗内壁里,有两个小球,分别在不同高度的水平面上做匀速圆周运动,这两个小球的质量分别为 m A m B A m A > m B θ A , B ω a v F N F 向
分析:
对小球受力分析可得:
{ F 合 = F N ⋅ cos θ F N ⋅ sin θ = m g ⟹ a = g cot θ
由于小球 A B θ a
那么由于 a a = ω 2 r r A > r B ω A < ω B a = r v 2 r A > r B v A > v B
根据受力分析可知 F N = sin θ m g m A > m B F N A > F NB
由于 F 向 = ma m A > m B F 向 A > F 向 B
对于任意同角不同面的匀速圆周运动模型,都有 a A A B
情况三:同面不同角(ω 如图所示,两小球 A , B A α B β A , B ω a v T
根据之前推得得结论可知 ω = L cos θ g L θ
根据图示可知,L cos θ = h ω = h g h A = h B ω A = ω B
根据 a = ω 2 r r A > r B a A > a B v = r ω r A > r B v A > v B T A > T B
【模型二】圆锥摆临界模型
临界问题最重要的是首先要排除是否有接触面给物体的支持力 F N ω
类型一
如图所示,一个绳子拉着一个小球在圆锥的外表面上做匀速圆周运动。求当角速度 ω
分析:当小球刚好要与接触面分离时,受到的接触面对小球的支持力 F N = 0
设圆锥摆壁与竖直直线的夹角为 θ
{ m g = T cos θ F 合 = T sin θ
又因为 F 合 = F 向 T sin θ = m ω 2 r ω = m r T sin θ = r g tan θ
类型二
如图所示,一个绳子拉着一个小球在水平面上做匀速圆周运动,求当角速度 ω
分析:当小球恰好要脱离水平面时,受到的水平面对小球的支持力为 F N = 0 θ ω = r g tan θ
易错点
当求出临界情况下的 ω ω ′ ω F N 必须重新受力分析 。
以上述类型二为例,当题目中的 w ′ > w 不再是 θ ,而是新的角度。
题目中出现「恰好绳子拉直」之类的字眼,一般视为此时绳子对物体的力为 0
例题
例 1:如图所示,在光滑的圆锥顶用长为 L m 2 θ ω = 2 L cos θ g T F N
分析:
首先求出对临界状态时的小球受力分析,求出小球脱离接触面临界状态时的 ω = L cos θ g
由于 2 L cos θ g < L cos θ g
对小球受力分析得:
{ F 合 = T sin θ − F N cos θ T cos θ + F N sin θ = m g
又因为 F 合 = F 向 = m ω 2 r = m ⋅ 2 L cos θ g ⋅ L sin θ = 2 1 m g tan θ
⎩ ⎨ ⎧ T sin θ − F N cos θ = 2 1 m g tan θ T cos θ + F N sin θ = m g ( 1 ) ( 2 )
将 ( 1 ) × sin θ + ( 2 ) × cos θ
T = 2 1 m g tan θ sin θ + m g cos θ
同理可得到 F N
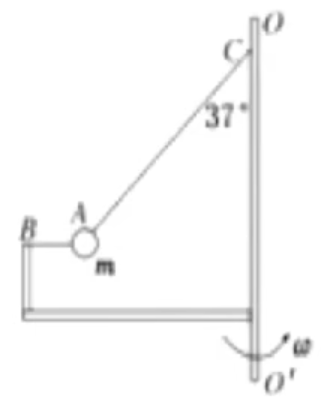
例 2:如图所示,小球 A A B A C θ = 3 7 ∘ m A C L B C BO O ′ O O ′ BO O ′
A. 两细线张力均增大
B. 细线 A B
C. 细线 A C
D. 当 A B 4 L 5 g
分析:
首先考虑对角速度为 0 A
{ T C sin 3 7 ∘ = T B T C cos 3 7 ∘ = m g
当 ω
{ F 合 = T C sin 3 7 ∘ − T B T C cos 3 7 ∘ = m g
再根据 F 合 = F 向 = m ω 2 r m ω 2 r = T C sin 3 7 ∘ − T B T C ω T B
当 T B 0 ω T C
当小球向上运动时,根据几何关系可知,绳子 A B A B A B
再对此时的小球受力分析得:
{ F 合 = T C sin 5 3 ∘ T C cos 5 3 ∘ = T B + m g
由于 F 合 = m ω 2 r T C T B
所以整个过程中 T C T B 0 0
观察选项可知 AB 错误,C 正确。
对于 D 选项,可知小球从初始状态(即将向上运动)到 AB 垂直(刚刚运动到垂直状态)的这段过程中,A B 0 ω 0
⎩ ⎨ ⎧ ω m i n = L cos 3 7 ∘ g = 4 L 5 g ω m a x = L cos 5 3 ∘ g = 3 L 5 g ⟹ 4 L 5 g ≤ ω ≤ 3 L 5 g
所以 D 正确。
总结:对于此类较复杂的圆锥摆问题,可以考虑将每个阶段的情况均受力分析,分段求解。
【模型三】圆盘模型
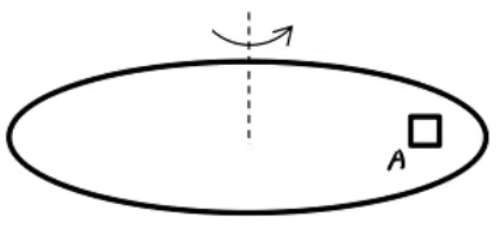
向心运动与离心运动
当物体在如下图所示的圆盘上做匀速圆周运动时,有 f = F 向 = m ω 2 r f ω f f 静 ≤ f 滑 = μ F N = μ m g f 静 = f 滑 f 滑 离心运动 ,此时 F 向 > F 合 = f 滑 f 滑 ω F 合
同理,当 F 合 > F 向 向心运动 。
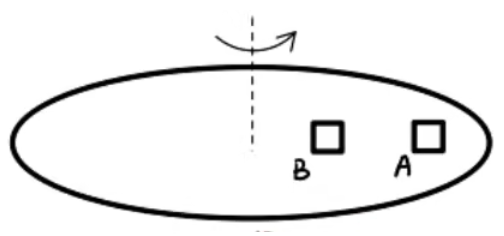
多物体模型之发生相对滑动的先后
如图所示,圆盘上有两个物体 A , B m A = m B μ A = μ B ω
对二者分别受力分析可得:
f A = m ω 2 r A f B = m ω 2 r B
由于 r A > r B f A > f B m A = m B , μ A = μ B f m a x f A > f B A B f m a x A
当 m A = m B ω A ω B
那么当 μ A = μ B A , B ω A = r A μ g , ω B = r B μ g r A > r B ω A < ω B A
多物体模型之同侧两物体
问题模型:如图,A B 同侧 ,一根绳子连接 A B m μ 0
绳子什么时候开始有拉力?
A , B 若剪断绳子,问 A , B
思路:一般从 ω = 0
分析:
对 ω = 0 F N = G
当 ω 0 f A f B f = m ω 2 r r f μ r A > r B A
所以当 A B
对此时的 A F 合 = f A + T f A
对此时的 B F 合 = f B − T f B ω F 合 f A T f B f B
那么对于第一问,当 A f m a x A f A = μ m g = m ω 2 r A ω 1 = r A μ g ω 1
对于第二问当 A , B A , B
{ T + μ m g = m ω 2 r A μ m g − T = μ ω 2 r B ⟹ 2 μ m g = m ω 2 ( r A + r B ) ⟹ ω = r A + r B 2 μ g
对于第三问,可对 A , B A , B ω A ω B ω ω ω A , B
多物体模型之异侧两物体
问题模型:如图,A B 异侧 ,一根绳子连接 A B m μ 0
绳子什么时候开始有拉力?
什么时候物体不受摩擦力?
什么时候发生相对滑动?
分析:
同样对 ω = 0 A , B F N = G A A B
那么当 A ω A F 合 = F 向 = T + f A f A T A T B T B 原来的摩擦力没有达到最大静摩擦力,本来就可以提供向心力,当存在绳子拉力 T B B 。
那么当 ω T ω 1 ω 2 A F 向 = T + f A T = F 向 − f A T 1 = m ω 1 2 r A T 2 = m ω 2 2 r A Δ T = m ( ω 2 2 − ω 1 2 ) r A B F 向 = m ω 2 r B F 1 = m ω 1 2 r B F 2 = m ω 2 2 r B Δ F 向 = m ( ω 2 2 − ω 1 2 ) r B r A > r B Δ T > Δ F 向 B F 合 = F 向 = T + f B T B f B
那么随着 ω f B f B 0 T B
当 ω T B F 合 = F 向 f B ω f B B f B
那么对于第一问,当 A f m a x A f A = μ m g = m ω 2 r A ω 1 = r A μ g ω 1
那么对于第二问,当 B T = F 向 B A , B
{ m ω 2 r A = T + f = T + μ m g T = m ω 2 r B ⟹ μ m g = m ω 2 ( r A − r B ) ⟹ ω = r A − r B μ g
对于第三问,当 A , B f m a x A , B
{ T + f A = T + μ m g = m ω 2 r A T − f B = T − μ m g = m ω 2 r B ⟹ 2 μ m g = m ω 2 ( r A − r B ) ⟹ ω = r A − r B 2 μ g
【模型四】火车拐弯
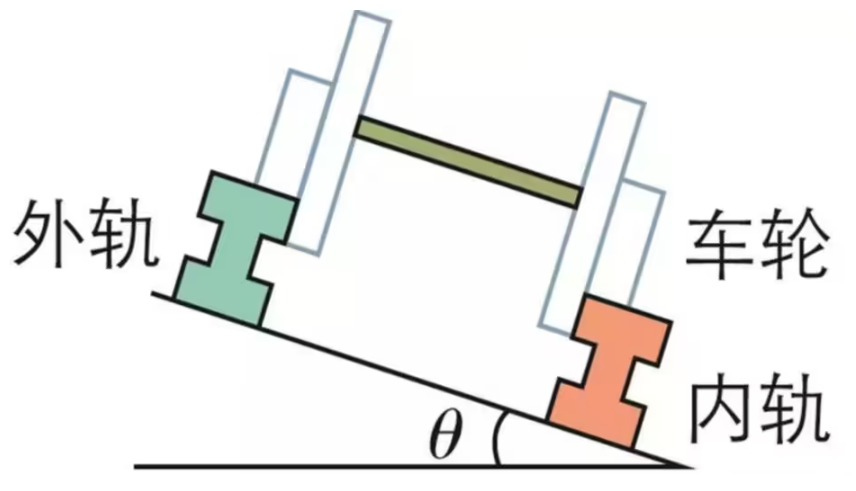
问题模型:如图所示,一火车在如图 1 所示的倒立圆台内壁 沿着红线做圆周运动,其弯道处的内外轨结构图示如图 2。问要使得火车车轮对内外规均无挤压作用,火车速度 v 0
分析:
对火车车轮受力分析,建立如图所示的坐标系:
那么有:
{ m a 0 = F N sin θ F N cos θ = m g ⟹ { F N = cos θ m g a 0 = g tan θ
根据 a 0 = r v 2 v 0 = g r tan θ
设火车车轮的速度为 v a
则当 v > v 0 a > a 0 F 向 > F 合
当 v < v 0 a < a 0 F 合 > F 向
【模型五】绳模型与杆模型
绳模型
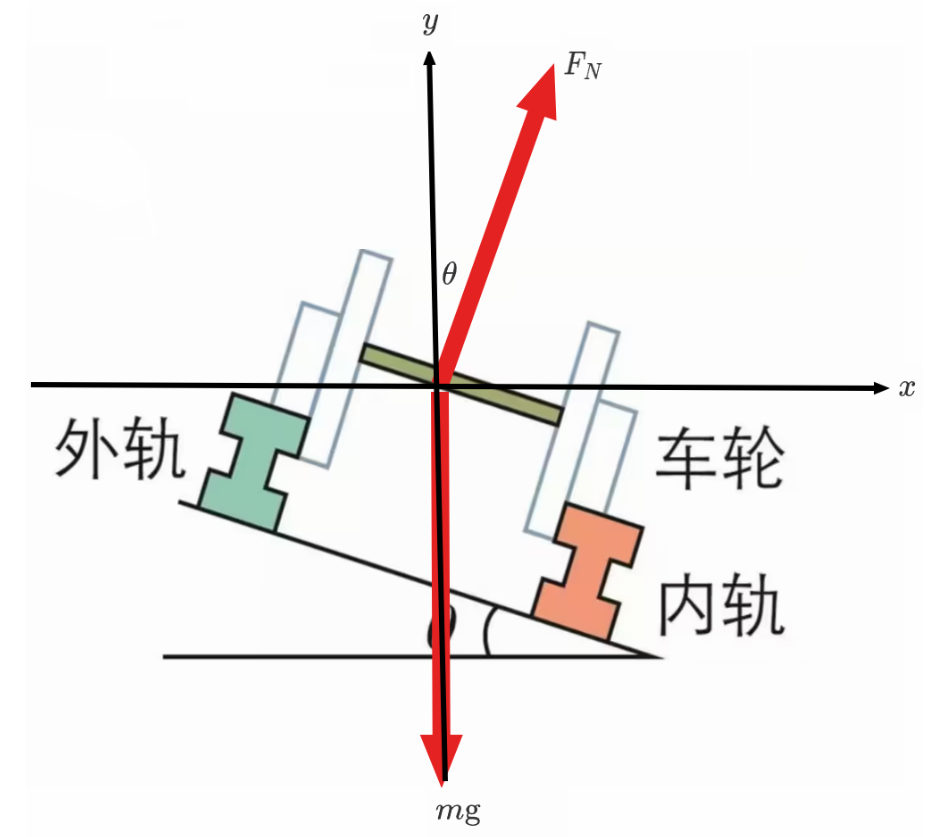
问题模型:一小球被绳 连接沿着如图所示的圆做匀速圆周运动,求小球运动到最高点时的最小速度至少为多少。
分析:对最高点的小球受力分析得 m g + T = m r v 2 T v T 0 v m i n = g r
结论:要使得小球做圆周运动,则最高点最小速度至少为 v m i n = g r
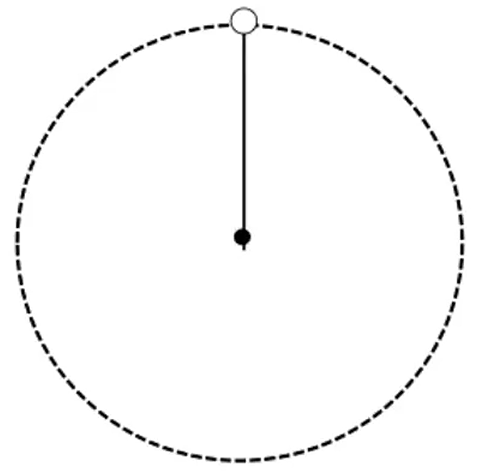
杆模型
问题模型:一小球被杆 连接沿着如图所示的圆做匀速圆周运动,求小球运动到最高点时的最小速度至少为多少。
分析:对最高点小球受力分析得 m g + F = m r v 2 F v v = 0 F = − m g
总结——绳与杆的区别:绳子最高点无支撑 ,杆最高点有支撑 。
题型:求杆对小球的力 F
首先求出当小球运动到最高点,F = 0 v 0 v = g r
设小球运动到最高点时的速度为 v
当 v > v 0 向上的支持力(压力) 。
当 v < v 0 向下的拉力 。
计算步骤:
首先算出临界速度 v 0 = g r
然后将小球速度 v v 0 F
对小球受力分析,求得 F
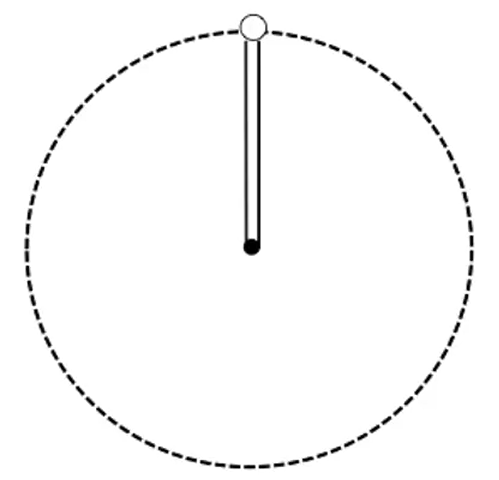
环模型
一般而言,有以下两种类型:
左边由于在最高点有支撑 ,所以属于杆模型,那么最高点的最小速度 v 0 = 0
右边由于在最高点无支撑 ,所以属于绳模型,那么最高点的最小速度 v 0 = g r
题型:求解左边模型下,速度为 v
分析:首先,小球不可能同时 受到内环和外环对它的力。考虑首先算出小球不受内外环对它的力时的速度 v 0




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!