【文化课学习笔记】【数学】复数

【数学】复数

定义

规定 \(i^2 = -1\)，并称 \(i\) 为虚数单位。则 \(i^3 = -i,i^4 = (i^2)^2 = 1,i^5 = i^4 \cdot i = i\)，所以 \(i^k\) 具有周期性，周期为 \(4\)。

复数：

\[z = a + bi(a,b \in \mathrm R) \]

其中 \(a\) 为实部，\(b\) 为虚部。注意：\(a\) 和 \(b\) 都是实数。

所有复数组成的集合就叫做复数集，即：

\[\mathrm C = \{z|z = a + bi,a,b \in \mathrm R\} \]

四则运算

四则运算的结果必须写为 \(a + bi\) 的形式。

一般地，设 \(z_1 = a + bi,z_2 = c + di(a,b,c,d \in \mathrm R)\)，则

\[z_1 + z_2 = (a + c) + (b + d)i\\ z_1 - z_2 = (a - c) + (b - d)i\\ z_1z_2 = (a + bi)(c + di) = ac + adi + bci + bdi^2 = (ac - bd) + (ad + bc)i\\ \dfrac{z_1}{z_2} = \dfrac{a + bi}{c + di} = \dfrac{(a + bi)(c - di)}{(c + di)(c - di)} = \dfrac{(ac + bd) + (bc - ad)i}{c^2 + d^2} \]

对于复数的除法，关键是消去分母的 \(i\)，若分母是 \(a + bi\)，则可以在分子分母上同乘 \(a - bi\)，将分母变为 \(a^2 + b^2\)；若分母是 \(ki\)，\(k \in \mathrm R\)则可以分子分母同乘 \(i\)，将分母变为 \(-ki\)。

运算性质

实数的所有运算性质，在复数中均成立。

1. 交换律，结合律和分配律。
2. 完全平方差公式，平方差公式。
3. 等式性质。

基本概念

做复数相关题目时，最关键的是要找到 \(a\) 和 \(b\)。

一般来说，复数题会给一个较为复杂的式子，需要化简式子并得到 \(a + bi\)，然后利用 \(a\) 和 \(b\) 解题。

若题目给定的是抽象复数，即没有给定具体的复数，那么可以考虑设对应复数 \(z = a + bi\)，根据基本概念表示出题目中相关的量代入求解。

分类

\[复数(a + bi) \begin{cases} 实数:b=0\\ 虚数:b \ne 0 \begin{cases} 纯虚数：a = 0 ~且~ b \ne 0\\ 实部不为 ~0~ 的虚数:a,b \ne 0 \end{cases} \end{cases} \]

注意：纯虚数需要保证 \(b \ne 0\)。

相等复数

实部与虚部都对应相等的复数，即：如果 \(a,b,c,d\) 都是实数，则 \(a + bi = c + di \iff a = c\) 且 \(b = d\)。

注意：两个复数，如果步全是实数，则无法比较大小。所以若题目给定两个复数的大小关系，则这两个复数一定都是实数。

复平面

建立了直角坐标系来表示复数的平面也称为复平面，一般对于复数 \(z = a + bi\)，令 \(Z\) 的坐标为 \((a,b)\)，则点 \(Z\) 是复数 \(Z\) 在平面上对应的点的坐标。

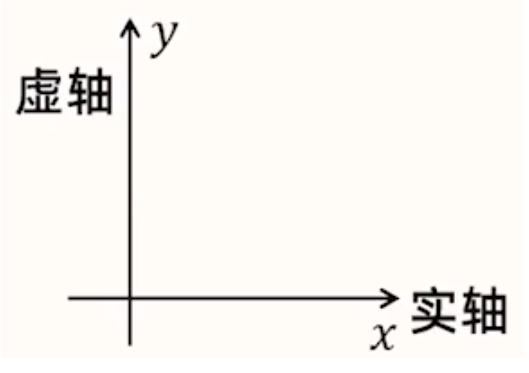
复数的几何意义

因为平面直角坐标系中的点 \(Z(a,b)\) 能唯一确定一个以原点 \(O\) 为始点，\(Z\) 为终点的向量 \(\overrightarrow{OZ}\)，所以复数也可用向量 \(\overrightarrow{OZ}\) 来表示。

因此能在复数集与平面直角坐标系中以 \(O\) 为始点的向量组成的集合之间建立一一对应关系，即 复数 \(z = a + bi \iff\) 向量 \(\overrightarrow{OZ} = (a,b)\)。

复数的模

向量 \(\overrightarrow{OZ} = (a,b)\) 的长度称为复数 \(z = a + bi\) 的模（或绝对值）。复数 \(z\) 的模用 \(|z|\) 表示 ，因此 \(|z| = \sqrt{a^2 + b^2}\)。

共轭复数

一般地，如果两个复数的实部相等，而虚部互为相反数，则称这两个复数互为共轭复数，复数 \(z\) 的共轭复数用 \(\overline{z}\) 表示。读作：\(z\) 共轭。

当 \(z = a + bi(a,b \in \mathrm R)\) 时，有 \(\overline z = a - bi\)。

【几何特点】复平面内表示两个复数的点关于实轴对称 \(\iff\) 两个复数互为共轭复数。

\(|z_1 - z_2|\) 的几何意义

内容

首先，\(|a-b|\) 表示数轴上 \(a,b\) 两点之间的距离。那么类比分析可知，\(|z_1 - z_2|\) 表示复平面上 \(z_1,z_2\) 两点之间的距离。

例如等式 \(|z - 1| = 1\)，实际上表示的是与点 \((1,0)\) 距离为 \(1\) 的点的集合，即圆心为 \((1,0)\)，半径 \(r = 1\) 的圆。

例题

例：复数 \(z\) 满足 \(|z + i| + |z - i| = 2\)，则 \(|z + i + 1|\) 的最小值是多少。

分析：

由于 \(|z + i|\) 和 \(|z - i|\) 分别表示平面内距离 \(A(0,-1)\) 和 \(B(0,1)\) 的点的坐标，设复数 \(z\) 在坐标系上对应的点为 \(P\)。则 \(|PA| + |PB| = 2\)，又由于 \(|AB| = 2 = |PA| + |PB|\)，所以点 \(P\) 的运动轨迹在线段 \(AB\) 上。

又由于 \(|z + i + i| = |z -(-1 - i)|\)，所以其几何意义为点 \(P\) 到 \(C(-1,-1)\) 的距离最小值。画图可知，当 \(CP \perp AB\)，即 \(P\) 与 \(A\) 共点时，距离最小，此时最小值为 \(1\)。

总结：遇到模长较多的题目，可以考虑将模长翻译成线段长度，从几何上解决问题。

复数的性质

性质一

内容：

\[|z_1z_2| = |z_1||z_2|\\ \left|\dfrac{z_1}{z_2}\right| = \dfrac{|z_1|}{|z_2|}(z_2 \ne 0) \]

作用：若题目中遇到模长的乘除法，则可以分别计算每个部分的模长，再算乘除法。

例如：

\[\left|\dfrac{3 + 2i}{2 + 3i}\right| = \dfrac{|3 + 2i|}{|2 + 3i|} = 1 \]

注意：这种性质只适用于乘除法，不适用于加减法。一般情况下，\(|z_1 + z_2| \le |z_1| + |z_2|\)。

例题：已知复数 \(z\) 满足 \(\left(\dfrac{1 + i}{\sqrt 2}\right)^{2019} z = \left(- \dfrac 1 2 + \dfrac{\sqrt 3}{2}i\right)^3\)，则 \(|z|\) 为多少。

分析：

由题意得：

\[z = \dfrac{\left(-\dfrac 1 2 + \dfrac{\sqrt 3}{2}i\right)^3}{\left(\dfrac{1 + i}{\sqrt 2}\right)^{2019}} \]

所以

\[\begin{aligned} |z| & = \dfrac{\left|\left(- \dfrac 1 2 + \dfrac{\sqrt 3}{2}i\right)^3\right|}{\left|\left(\dfrac{1 + i}{\sqrt 2}\right)^{2019}\right|}\\ & = \dfrac{\left|- \dfrac 1 2 + \dfrac{\sqrt 3}{2}i\right|^3}{\left|\dfrac{1 + i}{\sqrt 2}\right|^{2019}}\\ & = \dfrac{\left(\sqrt{\left(- \dfrac{1}{2}\right)^2 + \left(\dfrac{\sqrt 3}{2}\right)^2}\right)^3}{\left(\dfrac{|1 + i|}{|\sqrt 2|}\right)^{2019}}\\ & = \dfrac{1}{1} = 1 \end{aligned} \]

性质二

内容：

\[|z| = |\overline z|\\ z \cdot \overline z= |z|^2 \]

即两个共轭复数它们的模长相等，一个复数和它的共轭复数相乘，结果为该复数模长的平方。

适用范围：当题目中同时出现 \(|z|\) 和 \(|\overline z|\) 时可以考虑该性质。

复数的三角形式

对于复数 \(z = a + bi\)，其复平面上对应的点为 \(Z(a,b)\)，设 \(|z| = r\)，向量 \(\overrightarrow{OZ}\) 与 \(x\) 轴的夹角为 \(\theta\)，则复数 \(z\) 的三角表示为 \(z = r \cdot \cos \theta + r \cdot \sin \theta \cdot i = r(\cos \theta + i\sin \theta)\)。如图所示。

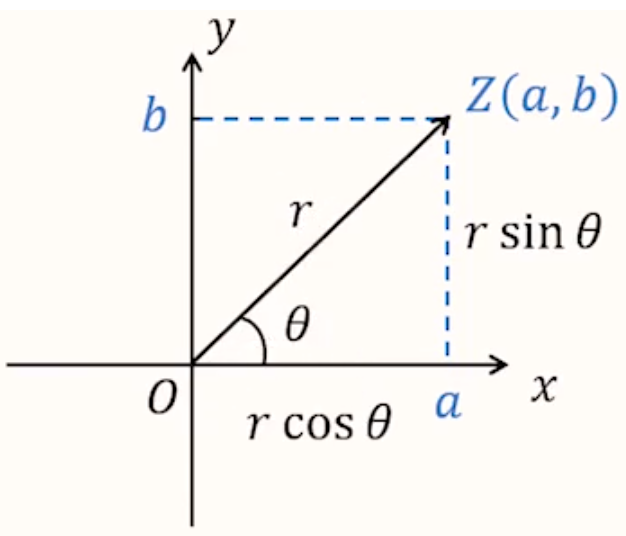
这里的 \(\theta\) 叫做辐角。任何一个非零复数 \(z\) 的辐角都有无穷多个。特别地，在 \([0,2\pi)\) 内的辐角称为 \(z\) 的辐角主值，记作 \(\arg z\)。